
- •Н.И. Николаева
- •Оглавление
- •Глава 1. Линейная алгебра
- •Матрицы и действия над ними
- •Линейные операции над матрицами
- •Транспонирование и умножение матриц
- •Определители и их свойства
- •Обратная матрица
- •Крамеровские системы уравнений
- •Ранг матрицы. Элементарные преобразования
- •Исследование произвольных систем линейных уравнений
- •Однородные системы линейных уравнений
- •Метод гаусса
- •Глава 2. Векторная алгебра векторы и линейные операции над ними
- •1. Сложение
- •2. Умножение на число
- •Проекция вектора на ось. Координаты вектора
- •Деление отрезка в данном отношении
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение веторов
- •Глава 3. Аналитическая геометрия прямая на плоскости. Общее уравнение прямой на плоскости
- •Уравнение прямой с направляющим вектором
- •Уравнение прямой с угловым коэффициентом
- •Угол между прямыми на плоскости
- •Расстояние от точки до прямой на плоскости
- •Кривые второго порядка. Окружность
- •Гипербола
- •Парабола
- •Преобразования координат на плоскости
- •Линейные преобразования на плоскости
- •Произведение линейных преобразований
- •Приведение квадратичной формы к каноническому виду
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •Плоскость
- •Особые случаи расположения плоскости
- •Уравнение плоскости в отрезках
- •Уравнение плоскости, проходящей через три точки
- •Угол между плоскостями
- •Прямая линия в пространстве
- •Канонические уравнения прямой в пространстве
- •Угол между прямыми в пространстве
- •Приведение общих уравнений прямой в пространстве к каноническому виду
- •Угол между прямой и плоскостью
- •Определение общих точек прямой и плоскости
- •Цилиндрические поверхности
- •Поверхности вращения
- •Библиографический список
Гипербола
ОПРЕДЕЛЕНИЕ. Гипербола – совокупность точек плоскости, модуль разности расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
Чтобы вывести
уравнение гиперболы, выберем пдск
следующим образом: ось абсцисс проведем
через фокусы
![]() и
и![]() ,
а ось ординат – посередине отрезка
,
а ось ординат – посередине отрезка![]() перпендикулярно оси абсцисс. Тогда
перпендикулярно оси абсцисс. Тогда![]() – фокусы гиперболы (рис. 30). Пусть
– фокусы гиперболы (рис. 30). Пусть![]() – произвольная точка, лежащая на
гиперболе.
– произвольная точка, лежащая на
гиперболе.
|
Х
Рис. 30 |
Запишем свойство точек, принадлежащих гиперболе, сформулированное в определении: |
![]() ,
(3.16)
,
(3.16)
(3.16) – уравнение гиперболы в выбранной системе координат ( «+» – если разность расстояний положительна, и «–» – если отрицательна). Чтобы привести это уравнение к более простому виду, умножим (3.16) на сопряженное выражение и выполним такие же действия, как при упрощении уравнения эллипса, после чего получим:
 .
(3.17)
.
(3.17)
По определению
![]() Обозначим
Обозначим![]() ,
тогда (3.17) перепишется в виде:
,
тогда (3.17) перепишется в виде:
 ,
(3.18)
,
(3.18)
(3.18) – каноническое уравнение гиперболы.
Исследуем форму гиперболы по ее каноническому уравнению.
Из (3.18) следует,
что гипербола симметрична относительно
осей координат. Если
 ,
значит, точек пересечения с
,
значит, точек пересечения с![]() нет; если
нет; если![]() ,
то
,
то![]() .
Точки пересечения с осями симметрии
называютсявершинами
гиперболы. Кроме того, из (3.18) следует,
что
.
Точки пересечения с осями симметрии
называютсявершинами
гиперболы. Кроме того, из (3.18) следует,
что
 .
Точка пересечения осей симметрии
называетсяцентром
гиперболы. Ось симметрии, на которой
расположены фокусы, называется фокальной
осью. При
этом фокальная ось также называется
действительной
(с ней
гипербола пересекается), а ось симметрии,
с которой гипербола не пересекается,
называется ее мнимой
осью.
.
Точка пересечения осей симметрии
называетсяцентром
гиперболы. Ось симметрии, на которой
расположены фокусы, называется фокальной
осью. При
этом фокальная ось также называется
действительной
(с ней
гипербола пересекается), а ось симметрии,
с которой гипербола не пересекается,
называется ее мнимой
осью.
![]() –полуфокусное
расстояние,
–полуфокусное
расстояние,
![]() –действительная
полуось,
–действительная
полуось,
![]() –мнимая
полуось.
Отношение полуфокусного расстояния к
длине действительной полуоси называется
эксцентриситетом
гиперболы:
–мнимая
полуось.
Отношение полуфокусного расстояния к
длине действительной полуоси называется
эксцентриситетом
гиперболы:
![]() .
Так как по определению
.
Так как по определению![]() ,
то
,
то![]() .
.
Считая, что
![]() из (3.18) получим, что
из (3.18) получим, что![]() – уравнение части гиперболы, расположенной
в первой четверти. Заметим, что при
неограниченном возрастании
– уравнение части гиперболы, расположенной
в первой четверти. Заметим, что при
неограниченном возрастании![]() разность
разность![]()
![]() ,
то есть при достаточно больших
,
то есть при достаточно больших![]() гипербола приближается к прямой
гипербола приближается к прямой![]() ,
причем ординаты точек на ней меньше
соответствующих ординат точек на этой
прямой:
,
причем ординаты точек на ней меньше
соответствующих ординат точек на этой
прямой:![]() .
Прямая
.
Прямая![]() называетсяасимптотой
гиперболы.
называетсяасимптотой
гиперболы.
|
b
-c -a О a c Х -b
Рис. 31 |
Из
симметрии гиперболы следует, что то
же самое происходит во второй, третьей
и четвертой четвертях. Поэтому
Итак,
прямые
|
Если фокусы
гиперболы лежат на
![]() ,
то ее уравнение имеет вид:
,
то ее уравнение имеет вид:
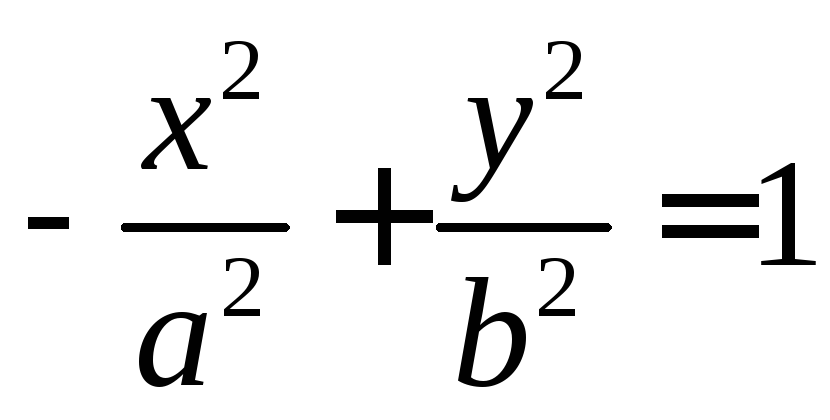 (3.19)
(3.19)
Гиперболы (3.18) и
(3.19) называются сопряженными (рис. 31).
Уравнения асимптот (3.19) такие же, как и
для (3.18), но действительной является ось
![]() .
.
Если
![]() ,
то гипербола называется равносторонней:
,
то гипербола называется равносторонней:![]() – уравнения ее асимптот (рис. 32 ).
– уравнения ее асимптот (рис. 32 ).
|
-a О a x
Рис. 32 |
Очевидно,
в этом случае асимптоты перпендикулярны.
После поворота осей координат на
ЗАМЕЧАНИЕ
1. Если
центр гиперболы в точке
|
ЗАМЕЧАНИЕ
2. К кривым
второго порядка гиперболического типа
относится также пара пересекающихся
прямых:
 .
.
ПРИМЕР.
Найти координаты центра и написать
уравнения асимптот гиперболы
![]() .
.
Приведем данное уравнение к виду (3.20):

Таким образом,
![]() – центр, а
– центр, а![]() – уравнения асимптот данной гиперболы.
– уравнения асимптот данной гиперболы.

 У
У У
У У
У .
. .
(3.20)
.
(3.20)