1.3. Определение системы передачи информации. Каналы связи.

Основной функцией информационной системы является хранение информации и ее перенос в пространстве. Совокупность технических средств для передачи сообщений от источника к потребителю называется системой связи. Этими средствами являются передающее устройство, линия связи и приемное устройство. Иногда в понятие система связи включаются источник и потребитель сообщений.

Структурная схема простейшей системы связи представлена на рисунке 2. Здесь исходным пунктом является источник сообщения. Источник может вырабатывать непрерывное или дискретное сообщения. Источником сообщений и получателем в одних системах связи может быть человек, в других — различного рода устройства (автомат, вычислительная машина и т. п.). Передача сообщений на расстояние осуществляется с помощью какого-либо материального носителя (бумага, магнитная лента и т.п.) или физического процесса (звуковых или электромагнитных волн, тока и.т.п.).

Источник информации или сообщения - это физический объект, система или явление, формирующие передаваемое сообщение.

Сообщение - это значение или изменение некоторой физической величины, отражающие состояние объекта (системы или явления). Как правило, первичные сообщения - речь, музыка, изображения, измерения параметров окружающей среды и т.д., представляют собой функции времени - f(t) или других аргументов - f(x, y, z) неэлектрической природы (акустическое давление, температура, распределение яркости на некоторой плоскости и т.п.).

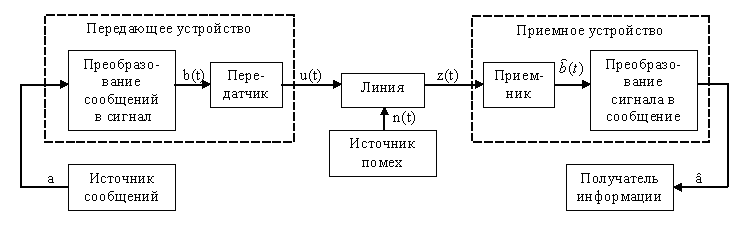
Рис.2. Структурная схема системы связи.

Каждое i - ое сообщение источника есть произвольная последовательность элементов алфавита (,, ...,) длинойm , где верхний индекс у элементов есть номер последовательности, а нижний индекс означает только место буквы в сообщении, но не ее вид.

При m = 1 сообщением является одна буква, то есть такое сообщение есть элементарное сообщение. В общем случае при m > 1 одна и та же буква может появиться в сообщении несколько раз. Общим свойством элементарного сообщения является его неделимость на более мелкие сообщения.

Конечное множество сообщений X c заданным на нем распределением вероятностей p(x) называется дискретным ансамблем сообщений и обозначается {X,p(x)}.

Устройство, преобразующее сообщение в сигнал, называют передающим устройством, а устройство, преобразующее принятый сигнал в сообщение, — приемным устройством.

С помощью преобразователя в передающем устройстве сообщение а, которое может иметь любую физическую природу (изображение, звуковое колебание и т.п.), преобразуется в первичный электрический сигнал b(t). В телефонии, например, эта операция сводится к превращению звукового давления в пропорционально изменяющийся электрический ток микрофона. В телеграфии сначала производится кодирование, в результате которого последовательность элементов сообщения (букв) заменяется последовательностью кодовых символов (0, 1 или точка, тире), которая затем с помощью телеграфного аппарата преобразуется в последовательность электрических импульсов постоянного тока.

В передатчике первичный сигнал b(t) (обычно низкочастотный) превращается во вторичный (высокочастотный) сигнал u(t), пригодный для передачи по используемому каналу. Это осуществляется посредством модуляции.

Преобразование сообщения в сигнал должно быть обратимым. В этом случае по выходному сигналу можно, в принципе, восстановить входной первичный сигнал, т. е. получить всю информацию, содержащуюся в переданном сообщении. В противном случае часть информации будет потеряна при передаче, даже если сигнал доходит до приемного устройства без искажений.

Физический процесс, отображающий (несущий) передаваемое сообщение, называется сигналом.

Сигнал – это материально-энергетическая форма представления информации. Другими словами, сигнал – это переносчик информации, один или несколько параметров которого, изменяясь, отображают сообщение.

Цепь “информация – сообщение – сигнал” – это пример процесса обработки, необходимой там, где находится источник информации. На стороне потребителя информации осуществляется обработка в обратном порядке: “сигнал – сообщение – информация”.

Любое преобразование сообщения в определенный сигнал путем установления между ними однозначного соответствия называют в широком смысле кодированием.

Кодирование может включать в себя процессы преобразования и дискретизации непрерывных сообщений (аналого-цифровое преобразование), модуляцию (манипуляцию в цифровых системах связи) и непосредственно кодирование в узком смысле слова. Обратная операция называется декодированием.

Линией связи называется среда, используемая для передачи сигналов от передатчика приемнику.

В системах электрической связи — это кабель или волновод, в системах радиосвязи — область пространства, в котором распространяются электромагнитные волны от передатчика к приемнику. При передаче сигнал может искажаться и на него могут накладываться помехи n(t).

Приемное устройство обрабатывает принятое колебание z(t)=u(t)+n(t), представляющее собой сумму пришедшего искаженного сигнала u(t) и помехи n(t), и восстанавливает по нему сообщение , которое с некоторой погрешностью отражает переданное сообщение a. Другими словами, приемник должен на основе анализа колебания z(t) определить, какое из возможных сообщений передавалось. Поэтому приемное устройство является одним из наиболее ответственных и сложных элементов системы связи.

Каналом связи называется совокупность средств, обеспечивающих передачу сигнала от некоторой точки А системы до точки В (рис. 3).

Точки А и В могут быть выбраны произвольно, лишь бы между ними проходил сигнал. Часть системы связи, расположенная до точки А, является источником сигнала для этого канала.

Рис. 3. Канал связи.

Канал как источник помех, оказывает на передаваемый сигнал некоторое влияние. Задачами приемника является выделение из зашумленного сигнала переданного сообщения и отправка его потребителю.

Классифицируют каналы связи по различным признакам, в том числе по математическому описанию (непрерывные и дискретные каналы, непрерывного и дискретного времени).

Если сигналы, поступающие на вход канала и принимаемые с его выхода, являются дискретными по состояниям, то канал называется дискретным. Если же эти сигналы являются непрерывными, то канал называется непрерывным. Встречаются также дискретно-непрерывные и непрерывно-дискретные каналы, на вход которых поступают дискретные сигналы, а с выхода снимаются непрерывные, или наоборот. Из сказанного видно, что канал может быть дискретным или непрерывным независимо от характера передаваемых сообщений. Более того, в одной и той же системе связи можно выделить как дискретный, так и непрерывный каналы. Все зависит от того, каким образом выбраны точки А и В входа и выхода канала.

В данном пособии будем рассматривать дискретный канал связи.

Если вредным действием помех в канале можно пренебречь, то для анализа используется модель в виде идеализированного канала, называемого каналом без помех. В идеальном канале каждому сообщению на входе однозначно соответствует определенное соотношение на выходе и наоборот. Когда требования к достоверности велики и пренебрежение неоднозначностью связи между сообщениями x и y недопустимо, используется более сложная модель – канал с помехами.

Простейший класс моделей каналов образуют дискретные каналы без памяти; они определяются следующим образом. Входом является последовательность букв (элементов) из конечного алфавита, пусть , выходом – последовательность букв того же самого или другого алфавита, скажем . Наконец, каждая буква выходной последовательности зависит статистически только от буквы, стоящей на соответствующей позиции во входной последовательности, и определяется заданной условной вероятностью, определенной для всех буквалфавита на входе и всех буквна выходе. Примером может служить двоичный симметричный канал (рис.4), который представляет собой дискретный канал без памяти с двоичными последовательностями на входе и выходе, в котором каждый символ последовательности на входе с некоторой вероятностью 1-q воспроизводится на выходе канала правильно и с вероятностью q изменяется шумом на противоположный символ. В общем случае, в дискретном канале без памяти переходные вероятности исчерпывают собой все известные сведения о том, как сигнал на входе, взаимодействуя с шумом, образует сигнал на выходе.

Рис. 4. Двоичный симметричный канал.

Намного более широкий класс каналов – каналов с памятью, образуют каналы, в которых сигналами на входе являются последовательности букв из конечных алфавитов, но в которых каждая буква на выходе может статистически зависеть не только от соответствующей буквы входной последовательности.