Подставим (3.7) в (3.4):

С учетом того, что , получим

(3.27)

Подставив (2.8) в (2.7), получим искомое выражение

(3.28)

В результате получили нормальный закон распределения вероятностей.

Выводы:

1. Если задана дисперсия состояний сообщений, то сообщение обладает наибольшей информативностью (максимальной энтропией) в том случае, когда состояния элементов распределены по нормальному закону.

2. Если задана средняя мощность помехи, то последняя является наиболее эффективной (энтропия помехи максимальна), когда состояния составляющих помеху элементов распределены по нормальному закону.

Второй случай. Определим вид функции w(x) , обеспечивающей максимальную энтропию сообщений при непрерывном распределении состояний элементов и произвольной дисперсии. Эта вариационная задача имеет только одно дополнительное условие.

(3.29)

Решение задачи можно получить, положив в (2.5) λ₂=0:

тогда уравнение (3.28) будет равно . Подставимw(x) в (3.29) и возьмем пределы a и b, так как w(x) не зависит от x:

,

откуда .

Так как функция плотности вероятности w(x) не зависит от x, то она является величиной постоянной во всем интервале существования случайной величины. Пусть состояния элементов сообщений существуют в интервале [a,b], тогда искомая функция распределения равна

(3.30)

внутри интервала [a,b] и нулю вне пределов его.

Выводы. Если дисперсия состояний сообщений не ограничена, то сообщения обладают наибольшей информативностью (максимальной энтропией) в том случае, когда состояния элементов распределены по равновероятному закону.

Для сравнения сообщений, удовлетворяющих нормальному и равновероятному законам распределения вероятностей, необходимо предварительно вычислить энтропию этих сообщений.

Вычислим энтропию сообщений, состояния элементов которых распределены по нормальному закону:

Т. к. , тои

(3.31)

Теперь найдем значение энтропии непрерывных сообщений для равновероятного закона распределения:

,,

. (3.32)

Рассмотрим два вида сообщений, обладающих одинаковой энтропией, но характеризуемых различными законами распределения состояний элементов: H_н(X) = H_р(X), где H_н(X)  энтропия сообщений с нормальным распределением, H_р(X)  энтропия сообщений с равновероятным распределением.

Согласно (3.31) и (3.32) , что приводит к равенству

(3.33)

Дисперсия для равновероятного закона распределения определяется интегралом . Обозначимx–x₀=₀, тогда dx = d, ,

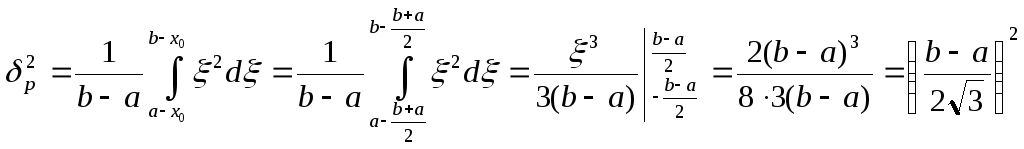
Откуда . Полученное выражение подставим в (3.14):

или .

Таким образом, если имеются две системы с одинаковыми значениями энтропии по величине, то дисперсия системы при равновероятном распределении на 42% больше дисперсии системы, имеющей нормальное распределение состояния элементов. Т. к. дисперсия характеризует среднюю мощность сигналов, то выгоднее передавать сообщения по нормальному закону распределения элементов. Затраты на мощность при нормальном законе будут составлять 0,7 по сравнению с затратами мощности при равновероятном законе распределения элементов.