1 (Бит), где m – мощность алфавита.

2) Элементы независимы и неравновероятны. Пусть, а. Тогда количество информации на один символ составит:

(бит).

3) Элементы взаимозависимы и неравновероятны. Пусть, например, Р(a) = 3/4, Р(b) = 1/4.

Пусть Р(a|a) = 2/3, Р(b|b) = 0 – вероятности повторения символов; Р(a|b) = 1, Р(b|a) = 1/3 - вероятности чередования символов.

Воспользуемся правилом P(X,Y) = P(X)∙P(Y|X).

P(a,a) = P(a)∙P(a|a) = 3/4∙2/3 = 1/2; P(a,b) = P(a)∙P(b|a) = 3/4∙1/3 = 1/4;

P(b,a) = P(b)∙P(a|b) = 1/4∙1 = 1/4; P(b,b) = P(b)∙P(b|b) = 1/4∙0 = 0.

I₃ = -1/2∙(1/2∙log1/2+1/4∙log1/4+1/4∙log1/4+0) = 0.75 (бит).

Глава 3. Энтропия дискретной последовательности. Энтропия непрерывной случайной величины

3.1. Частная энтропия

В теории информации чаще всего необходимо знать не количество информации I(x_i), содержащееся в отдельном сообщении, а среднее количе­ство информации в одном сообщении, создаваемом источником со­обще­ний.

Пусть требуется определить количество типичных последовательностей Q. Вероятность появления произвольной последовательности равна

.

В результате тождественных преобразований

Прологарифмировав последнее равенство, получим

где величина H(x)=-plog_mp-qlog_mq является характеристикой источника сообщений и называется э н т р о п и е й .

Покажем, что в случае типичных последовательностей ос­таточным членом О (п) по сравнению с величиной H(X) мож­но пренебречь.

Поскольку для типичных последовательностей справедливо неравенство , то

Следовательно,

.

Таким образом, при достаточно большом п справедливо приближенное равенство

.

Отсюда вероятность появления отдельной типичной после­довательности .

Поскольку правая часть равенства не зависит от номера ти­пичной последовательности k, то все типичные последователь­ности примерно равновероятны. Вероятность появления ти­пичной последовательности

где суммирование ведется по всему множеству типичных последовательностей. Отсюда

Q=m ^nH(X) ,

причем единица измерения энтропии Н (X) совпадает с осно­ванием степени т. Поскольку количество информации, нуж­ное для определения числа (состояния регистра), равно logQ, энтропия равна количеству информации, которое необходимо для определения состояния одного раз­ряда.

Аналогично определяется количество типичных последо­вательностей, вырабатываемых источником с алфавитом раз­мера т_X , только в этом случае энтропия

.

(3.1.)

Величину log1/P( можно рассматривать как частную энтропию, характеризующую информативность знака х_i, а энтропию H - как среднее значение частных энтропий.

Трактовать эту величину можно как среднее количество информации, приходящееся на один символ источника сообщения. Действительно, символы сообщения, как уже была сказано, несут разную информацию: если вероятность появления символа велика, он несет меньшую информацию, а если вероятность мала, то большую. Пусть имеются два состояния источника Y, имеющие соответственно вероятности р=0,001 и р=0999. Символ почти не несет информации, его появление практически предопределено. А вот появление символа - явление редкое.

Количественно энтропия равна средней информации. Однако качественно эти понятия противоположны. Несмотря на совпадение зависимостей, следует помнить, что энтропияН(X)и количество информацииI(X)принципиально различны. ЭнтропияН(X),выражающая среднюю неопределенность состояния источника сообщений является объективной характеристикой источника сообщений, и, если известна статистика сообщений, может быть вычислена априорно, т.е. до получения сообщения,I(X)является апостериорной характеристикой и определяет количество информации, получаемое с поступлением сообщений.Н(X) есть мера недостатка информации о состоянии отдельной системы. С поступлением информации о состоянии системы энтропия последней снижается. Совпадение выражения дляI(X)с выражением дляН(X)свидетельствует лишь о том, что количество получаемой информации равно численно энтропии, которая имела место относительно источника сообщений.

Н(х) объективно характеризует совокупность событий (источник сообщений) и может быть вычислена априорно. I(х) определяется апостериорно, т.е. после получения сообщения.

Следует сказать еще несколько слов о понятии энтропия. В литературе информационную энтропию часто отождествляют с энтропией термодинамической. Но это не так. Энтропия в теории связи была так названа только вследствие математической аналогии с энтропией, используемой в статистической механике. Но содержание этих двух понятий совершенно различно.

В математической теории связи рассматривается источник сообщений, который в определенной ситуации может создать любое из множества возможных сообщений. Количество информации, которое несет в себе сообщение, возрастает при увеличении количества неопределенности относительно того, какое сообщение из всех возможных будет выбрано. Одно из десяти возможных сообщений несет в себе меньшее количество информации, чем одно из миллиона. Энтропия в математической теории связи есть мара неопределенности, и эта неопределенность, или (что то же самое) энтропия берется в качестве меры количества информации, которое несет в себе сообщение от данного источника. Чем больше известно о том, какое сообщение будет создано источником, тем меньше неопределенность, тем меньше энтропия и тем меньше количество информации.

Поэтому, как советует Дж.Пирс «Чтобы понять, что такое энтропия в теории информации, лучше выкинуть из головы все, что связано с понятием энтропия, применяемое в физике».

Энтропия обладает следующими свойствами.

1. Чем больше неопределённость выбора сообщений, тем больше энтропия. Неопре­делённость максимальна при равенстве вероятностей выбора каждого сообщения: p(x₁)=p(x₂)= . . .=p(x_i)=1/k.

В этом случае

,

(т.е. максимальная энтропия равна логарифму от объёма алфавита).

Например, при k=2 (двоичный источник) бит.

2. Неопределённость минимальна, если одна из вероятностей равна единице, а остальные  нулю (выбирается всегда только одно заранее из­вестное сообщение, например,  одна буква): p(x₁)=1; p(x₂)= p(x₃)= ... = p(x_k)= 0. В этом случае H(X)=H_min(x)=0.

Эти свойства энтропии иллюстрируются следующим образом.

Пусть имеется двоичный источник сообщений, т.е. осуществляется выбор всего двух букв (k=2): x₁ и x₂, p(x₁)+ p(x₂)= 1.

Тогда

Зависимость H(X) от вероятностей выбора для двоичного источника приведена на рис. 5.

Рис. 5. Зависимость H(X) от вероятностей выбора для двоичного источника

3. Укрупним алфавит и предположим, что на выходе двоичного источника имеется устройство, которое группирует буквы в слова из n букв. Тогда k = 2ⁿ слов (объём алфавита). В этом случае

бит.

Таким образом, укрупнение алфавита привело к увеличению энтропии в n раз, так как теперь уже слово включает в себя информацию n букв дво­ичного источника. Тем самым доказывается свойство аддитивности энтро­пии.

4. Энтропия дискретного источника не может быть отрицательной.

Размерность энтропии  количество единиц информации на символ.

Пример 3.1. В первой урне имеются 7 белых, 5 черных и 2 синих шара. Во второй урне- 4 белых, 6 черных и 2 синих шара. Наудачу вынимают один шар. Для какой из урн исход более определенный?

Вычислим энтропию для каждого из случаев: шар – из первой урны, шар – из второй урны. Менее определенному исходу соответствует большее значение энтропии.

Решение. Для первой урны возможны три состояния: шар может оказаться или белым, или черным, или синим.

Найдем вероятность каждого состояния: белый шар р(б) =7/14=1/2; черный шар р(ч) = 5/14; синий шар р(с) = 2/14 =1/7.

Энтропия для первой урны:

Аналогичные расчеты выполним для второй урны. Вероятности состояний: р(б) =4/12= =1/3; р(ч) = 6/12 =1/2; р(с) = 2/12 =1/6.

Энтропия для второй урны:

Так как энтропия для второй урны меньше, значит исход для нее более определенный (получено меньшее количество информации).  

Пример 3.2. Пусть некто вынимает одну карту из колоды. Нас интересует, какую именно из 36 карт он вынул. Изначальная неопределенность составляет H=log₂(36)5,17 бит. Вытянувший карту, сообщает нам часть информации. Определим, какое количество информации мы получаем из этих сообщений.

Решение. Вариант A. “Это карта красной масти”.

I=log₂(36/18)=log₂(2)=1 бит (красных карт в колоде половина, неопределенность уменьшилась в 2 раза).

Вариант B. “Это карта  пиковой масти”.

I=log₂(36/9)=log₂(4)=2 бита (пиковые карты составляют четверть колоды, неопределенность уменьшилась в 4 раза).

Вариант С. “Это одна из старших карт: валет, дама, король или туз”.

I=log₂(36)–log₂(16)=5,17-4=1,17 бита (неопределенность уменьшилась больше чем в два раза, поэтому полученное количество информации больше одного бита).

Вариант D. “Это одна карта из колоды".

I=log₂(36/36)=log₂(1)=0 бит (неопределенность не уменьшилась - сообщение не информативно).

Вариант D. “Это  дама  пик".

I=log₂(36/1)=log₂(36)=5,17 бит (неопределенность полностью снята).

Пример 3.3. Имеется девять монет и весы, на которых можно сравнить вес монет. Одна монета фальшивая. Известно, что легче остальных. Какое минимальное число взвешиваний необходимо провести, что бы определить фальшивую монету? В каком порядке взвешивать монеты?

Решение. Процесс определения фальшивой монеты это случайное событие имеющее 9 равновероятных исходов. Энтропия этого события равна .

Определим максимальное количество информации, которое можно получить при одном взвешивании.

Если положить на чашки весов равное число монет, то возможны три исхода. Перевесит правая чашка, перевесит левая чашка, чашки в равновесии. Следовательно, взвешивание это случайное событие с тремя исходами. Энтропия этого события будет максимальной и равной в том случае, когда все три исхода имеют одинаковую вероятность.

Следовательно, минимальное число взвешиваний, выполнив которые можно получить количество информации равное или большее найдём из соотношения

,

где ближайшее кцелое число. В нашем случае k=2.

Порядок взвешивания монет должен быть таким, что бы каждое взвешивание давало максимально возможное количество информации.

Разделим 9 монет на три группы по 3 монеты в каждой. На правую чашку весов поместим первую группу монет, на левую – вторую группу. Если весы в равновесии, то фальшивая монета в третьей группе. Если не в равновесии, то в той чашке, которая поднялась.

При втором взвешивании поместим на весы по одной монете из подозрительной группы. Если весы в равновесии, то фальшивая монета та, которую не поместили на весы. Если весы не в равновесии, то фальшивая монета в той чашке, которая поднялась

Пример 3.4. Двоичный источник вырабатывает символ а1 с вероятностью р, а символ а2 – с вероятностью (1-р). Определить количество информации I(a_i) в каждом из символов а1 и а2 и энтропию источника, если p принимает следующие значения: 0.1, 0.2, 0.3, 0.4, 0.5.

Решение. Производим расчеты для p=0.1:

Аналогичные расчеты выполнены и для остальных значений. Их результаты приведены в таблице 3.1.

Таблица 3.1.

P	1-p	I(a1), бит	I(a2), бит	H(A), бит
0,1	0,9	3,322	0,152	0,469
0,2	0,8	2,322	0,322	0,722
P	1-p	I(a1), бит	I(a2), бит	H(A), бит
0,3	0,7	1,737	0,515	0,881
0,4	0,6	1,322	0,737	0,971
0,5	0,5	1,000	1000	1,000

График зависимости H(A) от вероятности p представлен на рис 6. Анализ полученных результатов показывает, что энтропия двоичного источника зависит от распределения вероятностей р(a_i). При их резкой асимметрии (р<0.2; (1-p)>0.8) энтропия невелика. По мере уменьшения разницы между вероятностями появления символов a1 и a2 энтропия источника возрастает и при p(a1)=p(a2)=-0.5 становится максимальной, равной 1 биту.

Рис 6. График зависимости H(A) от вероятности p.

Пример 3.5. Сравнить неопределенность, приходящуюся букву источника информации (алфавита русского языка), характеризуемого ансамблем, представленном в таблице, с неопределенностью, которая была бы у того же источника при равновероятном использовании букв.

Таблица 3.2.

Буква	Вероят-ность	Буква	Вероят-ность	Буква	Вероят-ность	Буква	Вероят-ность
а	0,064	й	0,010	т	0,056	ы	0,016
б	0,015	к	0,029	у	0,021	э	0,003
в	0,039	л	0,036	ф	0,02	ю	0,007
г	0,014	м	0,026	х	0,09	я	0,019
д	0,026	н	0,056	ц	0,04	пробел	0,143
е,ё	0,074	о	0,096	ч	0,013
ж	0,008	п	0,024	ш	0,006
з	0,015	р	0,041	ш	0,003
и	0,064	с	0,047	ъ,ь	0,015

Решение. 1. При одинаковых вероятностях появления всех m = 32 букв алфавита неопределенность, приходящаяся на одну букву, характеризует энтропия

H = log m = log 32 = 5 бит/симв.

2. Энтропию источника, характеризуемого заданным таблицей ансамблем

-0,064 log 0,064 -0,015log0,015 - ... - 0,143log0,143  4,43 бит/симв.

Таким образом, неравномерность распределения вероятностей использования букв снижает энтропию источника с 5 до 4,42 бит/симв.

Пример 3.6. Система X имеет равновероятных восемь состояний. Определить энтропию.

Решение. n = 8, (бит/символ).

Пример 3.7. На измерительной станции имеются два прибора. Первый имеет шкалу, содержащую 100 делений, его показания могут меняться через каждые 0.05 с. Шкала второго прибора имеет 10 делений, и его показания могут меняться каждые 0.01 с.

Какова наибольшая средняя информация, поставляемая двумя приборами в 1 с.?

Решение. 1-й прибор. Энтропия одного значения (отсчета) H₁(X) = log₂ m₁ = log₂100.

Число отсчетов в 1 с. n₁=1/0.05=20.

2-й прибор. Энтропия одного значения H₂(X) = log₂ m₂ = log₂10.

Число отсчетов в 1 с. n₂=1/0.01=100.

Энтропия двух приборов в 1 с.:

H_(X)=n₁H₁(X)+n₂H₂(X)=20 log₂ 100+100 log₂10=206.64+1003.32=464 бит/с.

Пример 3.8. Производится стрельба по двум мишеням, по одной сделано 2 выстрела, по второй – 3. Вероятность попадания при одном выстреле соответственно равны 1/2 и 1/3. Исход стрельбы (число попаданий) по какой мишени является более определенным?

Решение. Исход стрельбы определяется числом попаданий в мишень, которое подчинено биномиальному закону распределения:

p(X=m)=C_n^mp^m(1-p)^n-m, где C_n^m = n!/m!(n-m)!.

Составляем ряд распределения для числа попаданий в первую мишень при n=2 и p=1/2

m	0	1	2
p(x=m)	1/4	1/2	1/4

и во вторую мишень при n=3 и p=1/3

m	0	1	2	3
p(x=m)	8/27	4/9	2.9	1/27

Мерой неопределенности исхода стрельбы служит энтропия числа попаданий. Энтропия числа попаданий при стрельбе по первой мишени:

По второй мишени:

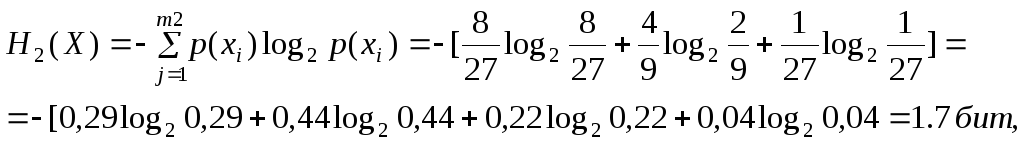
т.е. исход стрельбы по второй мишени обладает большей неопределенностью.

Пример 3.9. Источник генерирует знак z₁ с вероятностью 0.8 и z₂ с вероятностью 0.2. Какова энтропия источника?

Решение. H = - (0.8∙log₂0.8 + 0.2∙log₂0.2) = 0.72 (бит/символ).