Primery_reshenia_zadach_po_teme_2

Примеры решения задач по теме № 2

«Основы молекулярной физики и термодинамики»

Задача 1 Используя функцию распределения Максвелла по скоростям, найдите наиболее вероятное значение кинетической энергии атомов гелия, который при давлении р = 10⁵ Па имеет плотность =160 г/м³.

Дано: p = 105 Па  = 160 г/м3 = 0,16 кг/м3

-?

Решение

Запишем функцию распределения Максвелла по скоростям.

.

Поскольку нужно найти наиболее вероятное значение энергии, имеет смысл перейти от распределения по скоростям к распределению по энергиям f(). По смыслу функции распределения относительное число молекул, скорости которых лежат в интервале скоростей , которому соответствует интервал энергий , равно

.

Из данного выражения можно получить соотношение связывающее две функции распределения: . Из формулы видно, что для перехода от распределения по скоростям к распределению по энергиям недостаточно просто выразить скорость через энергию. Поскольку , , производная , и выражение для распределения по энергиям будет иметь вид

.

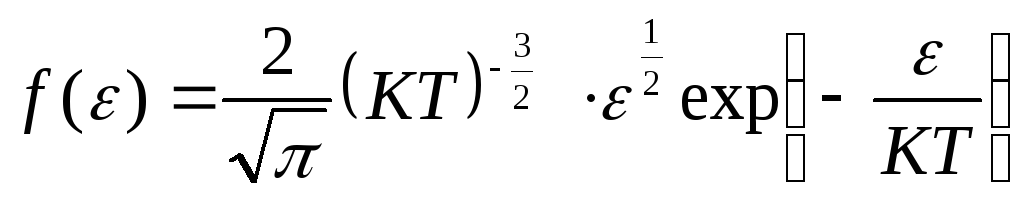Наиболее вероятное значение энергии соответствует максимуму функции распределения. Соответственно производная должна быть равна нулю:

, , , .

Обращаем внимание, что выражение наиболее вероятной энергии нельзя получить, подставив в формулу выражения наиболее вероятной скорости (в этом случае получилось бы ).

Из уравнения МенделееваКлапейрона следует, что , значит

(в последней формуле учтено, что R = N_A·k). Подставляя данные из условия и молярную массу гелия = 4·10^-3 кг/моль, получим Дж.

Ответ: Дж.

Задача 2 Пылинки массой 10^-18 г взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1%. Температура воздуха во всем объеме одинакова: Т=300 К.

Дано:

m1 = 10-21 кг T = 300 К	Решение При равновесном распределении пылинок их концентрация зависит только от координаты z по оси, направленной вертикально. По распределению Больцмана: n=n0e-u/kT=n0e-mgz/kT. (1) Дифференцируя выражение (1) по z, получим
Z - ?

dn=-n_0e^-mgz/kTdz.

Так как n₀e^-mgz/kT=n, то dn=ndz. Отсюда .

Знак «-» показывает, что положительным изменениям координаты (dz>0) соответствует уменьшение относительной концентрации (dn<0). Знак «-» опускаем и заменяем dz и dn конечными приращениями z и n:

.

n/n=0,01 по условию задачи. Подставляя значения, получим z=4,23 мм.

Ответ: z=4,23 мм.

Задача 3 В сосуде объёмом V = 1 л находится углекислый газ массой m = 0,2 г. При температуре T =2600 K некоторая часть молекул диссоциировала на молекулы кислорода и окиси углерода. При этом давление газа в сосуде оказалось равным 108 кПа. Определить, какая часть молекул диссоциировала.

Дано: V = 1 л = 10-3 м3 m = 0,2 г = 210-4 кг Т = 2600 К Р = 108 кПа = 1,08105 Па

α -?

Решение

Рассмотрим уравнение диссоциации углекислого газа

Таким образом, каждый моль углекислого газа, распадаясь вызывает появление одного моля окисла углерода и половину моля кислорода. В результате распада части молекул в сосуде будут находиться три газа: CO₂, CO, O₂.

По закону Дальтона найдём выражение для давления, создаваемого данной смесью газов

.

Введём степень диссоциации - отношение числа молей распавшихся молекул к начальному числу молей вещества . Тогда число молей CO₂

,

число молей CO ,

число молей O₂ (с учётом уравнения реакции) .

Из уравнения Менделеева–Клапейрона

, , .

Общее давление будет связано со степенью диссоциации уравнением

.

Так как ( = 44·10^-3 кг/моль – молярная масса CO₂), то . Выражая и производя расчет, получим .

Ответ:  = 0,2.

Задача 4 В результате некоторого процесса вязкость некоторого идеального газа увеличилась в раза, а коэффициент диффузии – в раза. Во сколько раз увеличи­лось давление газа.

Решение

Дано:

-?

Согласно молекулярно кинетической теории,

, ,

где  средняя длина свободного пробега,

- средняя скорость движения молекул,  = m₀n  плотность газа.

По основному уравнению МКТ , поэтому . Подставим в выражение  значения , и , тогда

.

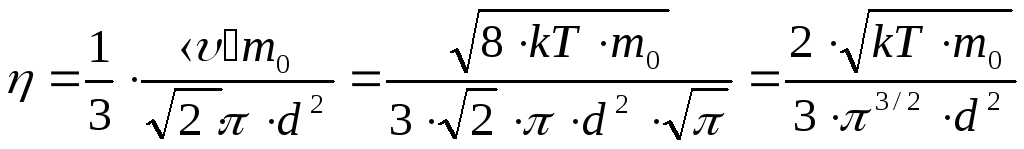Из формул видно, что ~, значит, . Для того чтобы найти отношение , свяжем между собой и D. Из формул видно, что . Отсюда , а отношение . В итоге получаем отношение давлений .

Ответ: давление возрастет в два раза.

Задача 5 Газ, занимавший объем 2 л при давлении 0,1 МПа, расширился изотермически до 4 л. После этого, охлаждая газ изохорически, уменьшили давление в 2 раза. Далее газ изобарически расширился до 8 л. Начертите график зависимости давления от объема, найдите работу, совершенную газом.

Дано: V1 = 2 л = 210-3 м3 P1= 0,1 МПа = 0,1106 Па V2 = 4 л = 410-3 м3 P3 = V3 = 8 л = 810-3 м3

A - ?

Решение

Построим график зависимости давления от объема. Первый процесс, происходящий с газом, является изотермическим. Выразим давление через объём и температуру при помощи уравнения Менделеева – Клапейрона . Так как T = const, давление в данном процессе обратно пропорционально объёму, и линия, изображающая данный процесс на p-V диаграмме, будет участком гиперболы начинающейся в точке V₁, p₁ и заканчивающейся в точке V₂, p₂.

Второй процесс, происходящий с газом, является изохорическим. В этом процессе объём не изменяется и, следовательно, на P-V диаграмме он изображается в виде вертикальной прямой, идущей из точки V₂, p₂ в точку V₂, p₃.

Третий процесс происходящий с газом, по условию задачи, изобарический. На P-V диаграмме он будет выглядеть как горизонтальная линия, идущая из точки V₂, p₃ в точку V₃, p₃.

Последовательно изображая все процессы, получим следующую P-V диаграмму.

Рассчитаем работу, совершенную газом. Так как работа, совершаемая газом,  аддитивная величина

А = А₁+А₂+А₃ ,

где А₁ – работа, совершенная в изотермическом процессе,

А₂ – работа, совершенная в изохорическом процессе,

А₃ – работа, совершенная в изобарическом процессе. Каждую из работ можно вычислить по формуле (V₁ и V₂ – начальные и конечные объёмы, занимаемые газом). Применим эту формулу для определения работы А₁. Согласно уравнению Менделеева – Клапейрона, зависимость p(V) имеет вид .

Следовательно, работа . Множитель RT вынесем из-под знака интеграла как постоянную величину, заменяя её на p₁V₁, получим

.

В изохорическом процессе изменение объёма газа не происходит, следовательно, А₂ = 0.

При вычислении работы А₃ учтём, что давление, как постоянная величина, может быть вынесена из под знака интеграла

.

Для расчёта необходимо знать давление P₃. Так как первый процесс изотермический, . По условию задачи , следовательно,

.

Общая работа А = А₁+А₂+А₃ = 238,63 Дж.

В качестве дополнения заметим, что существует еще один способ определения работы, совершаемой газом, – графический. Как известно, площадь на диаграмме pV между линией, изображающей процессы, происходящие с газом, и осью объема по модулю равна работе. Если объём газа увеличится, то работа положительна, в противном случае  отрицательна. В ряде случаев этот метод позволяет найти работу, не прибегая к вычислению интегралов.

Ответ: А = 238,63 Дж.

Задача 6 Определите показатель адиабаты  для смеси газов, содержащей гелий массой = 8 г и водород массой = 2 г. Газы считать идеальными.

Дано: = 8г. 1= 4·10-3 кг/моль = 2г. 2 = 2·10-3 кг/моль

-?

Решение

По определению . Рассчитаем удельные теплоёмкости для смеси газов. Первой вычислим теплоёмкость при постоянном объёме. Количество теплоты, необходимое для нагревания смеси газов на ΔT, с одной стороны, по определению теплоёмкости, равно .

С другой стороны, данное количество теплоты может быть представлено как сумма теплот, идущих на нагревание двух газов по отдельности:

.

Приравнивая выражения, получим .

Удельные теплоёмкости газов можно выразить через число степеней свободы молекул и молярные массы газов:

; ,

где = 3, = 5.

После подстановки получаем .

Аналогичные рассуждения дадут для удельной теплоёмкости при постоянном давлении

.

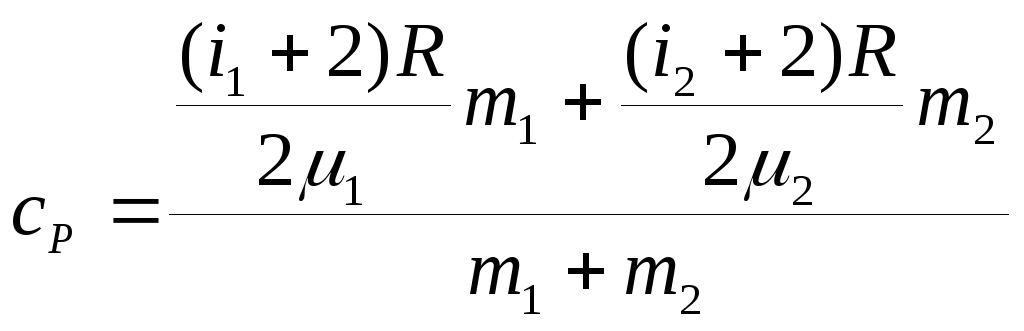Соответственно показатель адиабаты после подстановки полученных выражений

.

Ответ: .

Задача 7 Определить КПД тепловой машины, работающей по циклу, изображенному на рисунке, если известно, что V₂ = 2V₁, Т₂ = 2Т₁, а рабочим телом является идеальный трехатомный газ.

Дано: Т2 = 2Т1 V2 = 2V1

-?

Решение

Прежде всего проанализируем процессы, происходящие с газом. Процессы 2 – 3 и 4 – 1, как видно из рисунка, являются изохорическими. В процессах 1 – 2 и 3 – 4 температура прямо про­порциональна объёму. Значит, данные процессы являются изобарическими.

П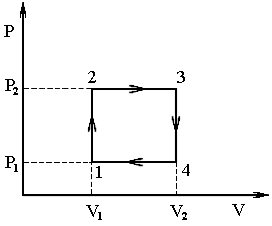ерерисуем цикл машины в координатах p–V. По условию задачи температуры в начале и конце изохорического процесса отличаются в 2 раза. Значит, во столько же раз должны отличаться давления газа и можно записать, что

p₂ = 2p₁.

КПД цикла, по определению, равен отношению работы, совершенной газом, к количеству теплоты, полученной от нагревателя: .

Работа, совершаемая газом за цикл, численно равна площади, ограничиваемой циклом на диаграмме p-V. В данном случае эта площадь представляет собой прямоугольник, следовательно:

A = (p₂ - p₁)(V₂ - V₁) = p₁V₁.

Тело получает теплоту от нагревателя на участках 1-2 и 2-3 (на участках 3-4 и 4-1 рабочее тело тепловой машины отдаёт теплоту холодильнику): Q_н = Q₁₂ + Q₃₄.

Рассчитаем количество теплоты Q₁₂ = С_V(T₂ - T₁). С_V = 3R  молярная теплоемкость трёхатомного газа при постоянном объёме. Учтем, что для трёхатомного газа число степеней свободы i = 6. Т₁ и Т₂ температуры в соответствующих точках цикла. Раскрывая скобки и учитывая, что RT₁ = p₁V₁; RT₂ = p₂V₁ = 2p₁V₁, получим

Q₁₂ = 3R(T₂-T₁) = 3 (RT₂- RT₁) = 3(2p₁V₁ - p₁V₁) =3 p₁V₁.

Аналогично, можно записать Q₂₃ = С_p(T₃-T₂). С_р = 4R – молярная теплоёмкость трёхатомного идеального газа при постоянном объёме. Учитывая, что

RT₃ = p₂V₂ = 4p₁V₁,

запишем

Q₂₃ = 4R(T₃-T₂) = 4(4p₁V₁ – 2p₁V₁) = 8p₁V₁, Q_Н = Q₁₂ + Q₂₃ = 11 p₁V₁.

Рассчитаем коэффициент полезного действия .

Ответ: .

Задача 8 В двух сосудах одного и того же объёма находится гелий массой 10 г (₁= 4·10^-3 кг/моль) и азот массой 56 г (₂ = 28·10^-3 кг/моль). Давление и температура газов одинаковы. Сосуды соединяют и начинается процесс диффузии. Определить изменение энтропии системы в данном процессе.

Дано: m1 = 10 г =0,01 кг 1 = 4 г/моль = 0,004 кг/моль m2 = 56 г = 0,056 кг 2 = 28 г/моль = 0,028 кг/моль

ΔS -?

Решение

Процесс диффузии в данной задаче можно рассматривать как процесс изотермического расширения. В этом случае изменение энтропии гелия

.

Так как процесс изотермический, Q₁ = A₁. Вычисляя работу в изотермическом процессе, получим

.

В последней формуле учтено, что V₂ = 2V₁, так как по условию объёмы обоих сосудов равны. Следовательно, .

Аналогичные вычисления для второго газа дают .

Полное изменение энтропии всей системы

.

Ответ: .

9