35. Связь напряженности и потенциала электростатического поля в интегральной и дифференциальной форме

Потенциал произвольной точки поля может быть определен как работа, совершаемая силами поля по переносу единичного положительного заряда из данной точки поля в точку поля потенциал которой равен нулю.

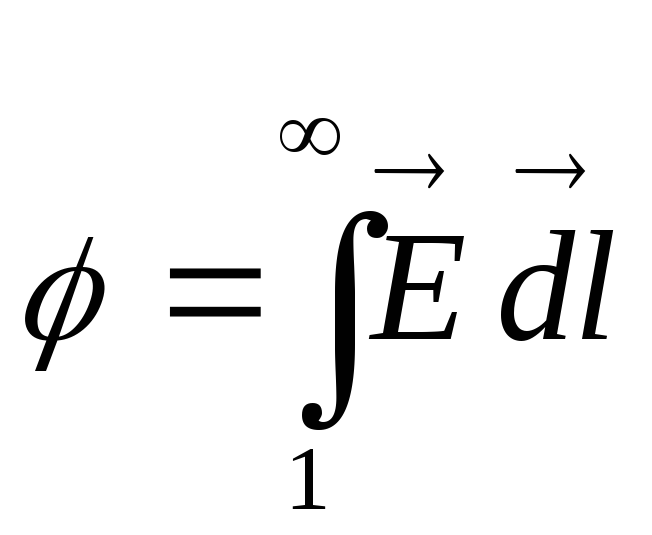
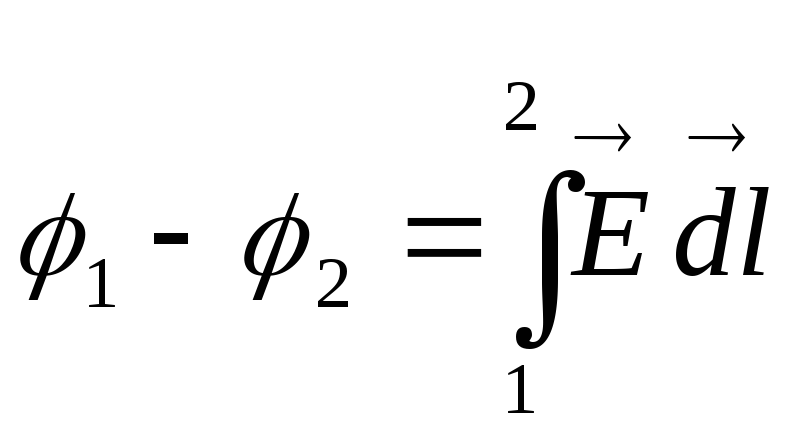
36. Теорема Гаусса в интегральной и дифференциальной форме

Теорема Гаусса является одной из важнейших теорем электростатики. Она может быть сформулирована и записана тремя способами:

1. Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности

2. Так как 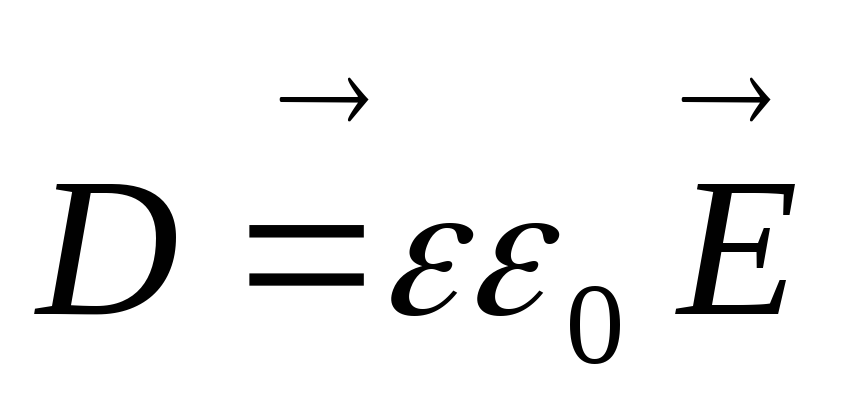, то теорема Гаусса для однородной и изотропной среды может быть записана в такой форме

3. Существует ещё одна форма записи теоремы Гаусса, отличающаяся от двух предыдущих

Дело в том, что поток вектора через любую замкнутую поверхность создается не только суммой свободных зарядов, но и связанных, находящихся внутри этой поверхности. Теорема Гаусса, записанная в интегральной форме, выражают связь между потоком вектораи алгебраической суммой зарядов, находящихся внутри этого объема. При помощи теоремы Гаусса в интегральной форме нельзя определить как связан источник линийв данной точке поля с плотностью свободных зарядов в той же точке поля. Ответ на этот вопрос даёт дифференциальная форма теоремы Гаусса.

1. 

2. 

3. 

37. Запись условия потенциальности электростатического поля в интегральной и дифференциальной форме

38. Закон Ома в Дифференциальной форме

- закон Ома в дифференциальной форме

Он устанавливает связь между плотностью тока в данной точке проводящей среды и напряженностью поля в этой точке.

39. Первый закон Кирхгофа в интегральной и дифференциальной формах

Сумму входящего в объем и выходящего из объема токов записывают так , иначе в этом объеме происходило бы накопление зарядов, что опыт не подтверждает. Это соотношение называют первым законом Кирхгофа в дифференциальной форме. Оно означает, что в установившемся режиме в любой точке поля нет ни истока, ни стока линий.

40. Первое уравнение Максвелла

Первое уравнение Максвелла записывают следующим образом

В правой части имеется две плотности тока: плотность тока проводимости и плотность тока электрического смещения.

Таким образом смысл первого уравнения Максвелла состоит в том, что всякое изменение напряженности электрического поля во времени () в некоторой точке поля на таких же правах, как и ток проводимости, вызывает в этой точке вихрь поля магнитного (), т.е. вызывает вихревое магнитное поле

41. Второе уравнение Максвелла

Второе уравнение Максвелла записывают следующим образом

Физический смысл его состоит в том, что всякое изменение магнитного поля во времени () в какой-либо точке поля вызывает вихревое поле. Второе уравнение Максвелла представляет собой дифференциальную форму закона электромагнитной индукции.

42. Объемная плотность энергии электромагнитного поля

43. Теорема Умова-Пойнтинга

Теорема Умова-Пойнтинга для мгновенных значение записывают следующим образом

Левая часть – поток вектора Пойнтинка внутрь объема;

- энергия, выделяющаяся в виде теплоты в еденицу времени в объемеV;

dv– скорость изменения запаса энергии в единице объема