
- •Методические указания по решению задач
- •1.2.Консервативные и неконсервативные силы.
- •1.3. Кинетическая энергия при поступательном и вращательном движениях.
- •1.4. Потенциальная энергия.
- •2. Законы сохранения в механике.
- •2.1. Закон сохранения механической энергии.
- •2.2. Закон сохранения импульса. Удар двух тел.
- •2.3. Закон сохранения момента импульса.
- •Примеры решения задач.
- •Решение
- •Задачи, рекомендуемые для решения на аудиторных занятиях
- •Домашнее задание
- •Краткие теоретические сведения для решения задач.
- •2.2. Следствия из преобразований Лоренца.
- •Примеры решения задач
- •Задачи, рекомендуемые для решения на аудиторных занятиях
- •Домашнее задание
- •Варианты домашнего задания
- •Номер варианта соответствует порядковому номеру студента в журнале группы.
- •Редактор в. А. Маркалева
Примеры решения задач
Пример 1. В условно неподвижной системе отсчета К в точках с координатами xA и xB = xA + l, где l = 1 км, одновременно происходят два события A и B. На каком расстоянии lАВ друг от друга зафиксирует эти события наблюдатель в системе К, движущейся со скоростью v = 0,4с вдоль оси X? Какой промежуток времени t между этими событиями зафиксирует наблюдатель в системе К?
Р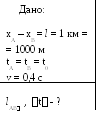 ешение
ешение
Обозначим через t0 момент времени, когда в системе К происходят события А и В. Тогда событие А в этой системе обладает пространственно – временными координатами xA и t0, а событие В – координатами xB и t0. В системе К событие А обладает пространственно–временными координатами x1 и t1, а событие В – координатами x2 и t2. Связь координат каждого из событий можно записать с помощью преобразований Лоренца.
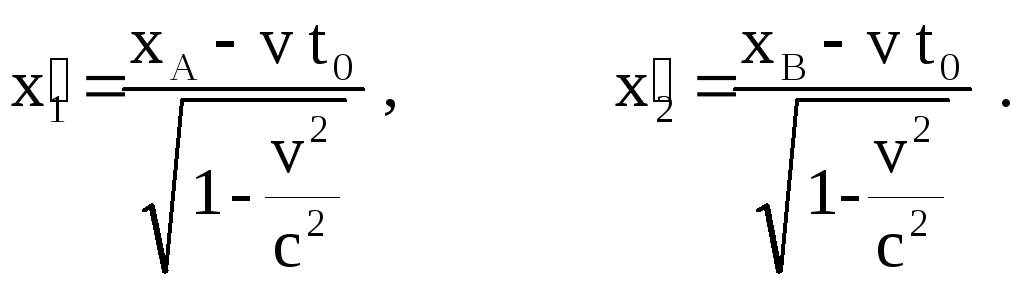
Найдя разность этих выражений, получим расстояние между точками,в которых происходят события А и В в системе К.

Видно, что расстояние lАВ, разделяющее события А и В в любой системе, движущейся относительно К, больше, чем это же расстояние, измеренное в системе К, в которой оба события одновременны. Рассчитаем расстояние lАВ.
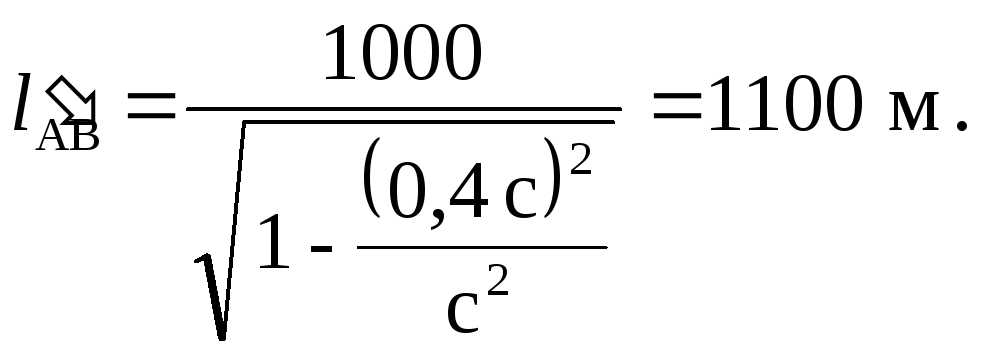
Моменты времени, в которые в системе Кнаблюдатель зафиксирует события А и В, также могут быть найдены из преобразований Лоренца:
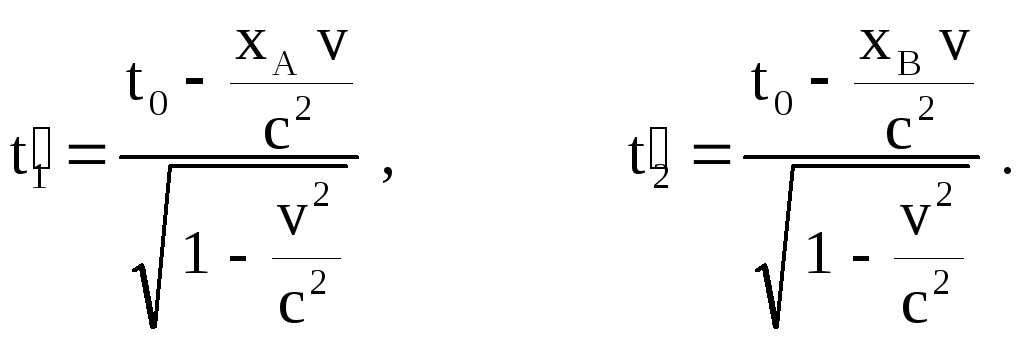
Тогда
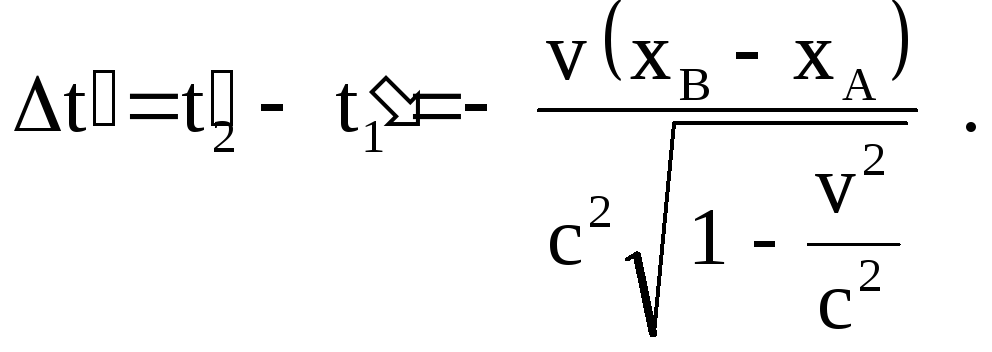
Видно, что события А и В в системе отсчета К не являются одновременными. Если xB xA и система К движется в положительном направлении оси X, как и задано в условии, то t2 - t1 0, то есть событие В происходит раньше, чем событие А. Рассчитаем t.
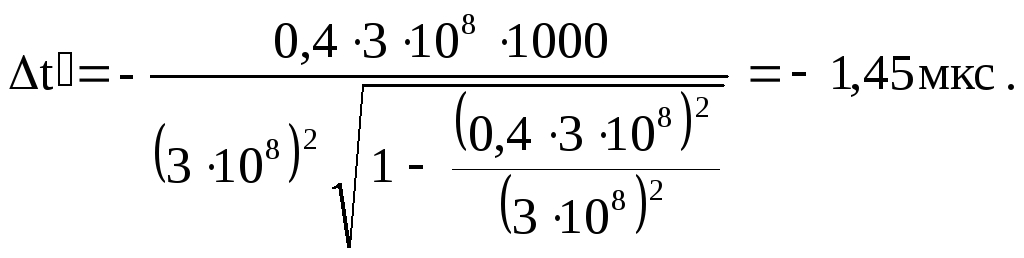
То есть событие В, зафиксированное наблюдателем в системе К, опережает событие А на 1,45 мкс.
Ответ: lАВ = 1100 м; t = - 1,45 мкс.
Пример 2. В системе отсчета К, движущейся со скоростью v0 = 0,5 с вдоль оси X неподвижной системы К, расположен неподвижный стержень длиной l = 1 м, ориентированный под углом = 30о к оси X. Параллельно стержню летит частица со скоростью v = 0,4 с. Под каким углом к оси X ориентирован этот стержень для наблюдателя в системе К? Под каким углом к оси X летит частица в системе К?
Р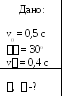 ешение
ешение
Рассмотрим вначале стержень с точки зрения наблюдателя в системе К. Он движется поступательно с горизонтальной скоростью vx = v0 = 0,5 c. Вследствие этого стержень в горизонтальном направлении сжат, в вертикальном направлении его размеры неизменны. Следовательно, длина стержня для наблюдателя в системе К будет меньше, чем для наблюдателя в системе К, а угол наклона стержня к оси X больше чем . Применим следствия из преобразований Лоренца для нахождения расстояний между проекциями концов стержня на оси X и Y:
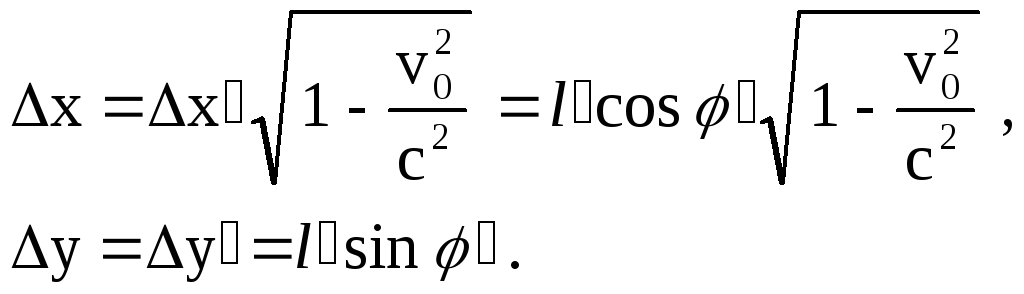
Стержень образует с осью X угол , причем tg = y/x.
Тогда выражение для tg примет вид:
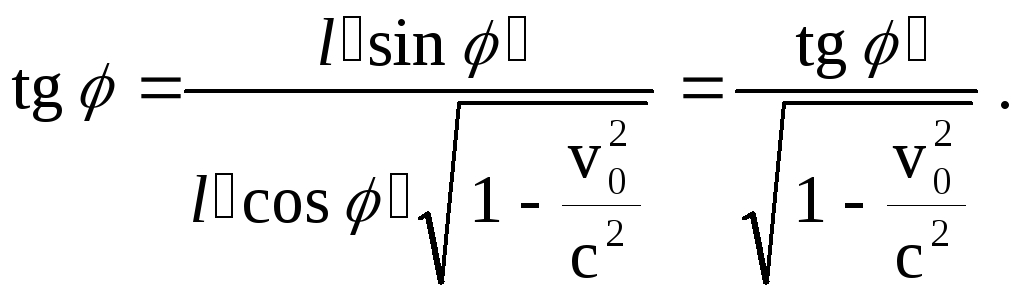
Сделаем вычисления:
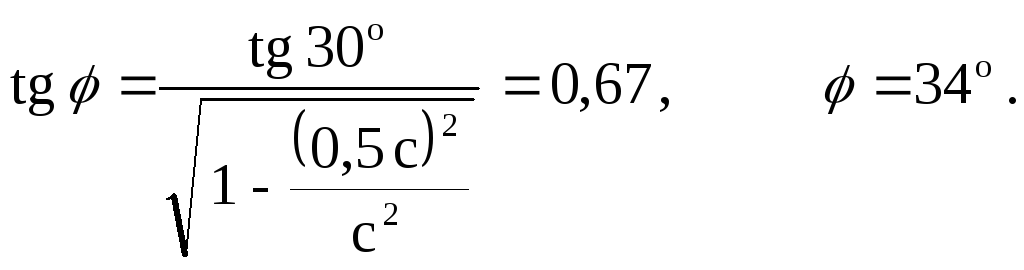
Теперь рассмотрим движение частицы. Частица, в отличие от стержня, движется относительно системы К и горизонтальная составляющая ее скорости vx отличается от vx = v cos . Причем если vx 0, то очевидно, vx больше чем vx. Вертикальная составляющая скорости частицы vy меньше чем vy = v sin . Поэтому скорость v частицы образует с осью X угол, не равный . Таким образом, для наблюдателя в системе К частица будет двигаться прямолинейно, но уже не параллельно стержню. Проекции скорости частицы на оси X и Y могут быть получены как следствие из преобразований Лоренца:
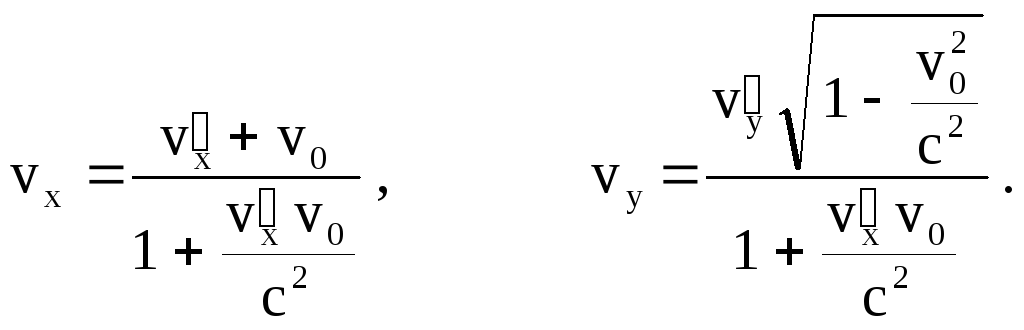
Вектор скорости частицы образует с осью X угол = arctg (vy/vx). Учитывая формулы для vx и vy и выражая проекции скоростей vx и vy через скорость v и тригонометрические функции угла , получаем:
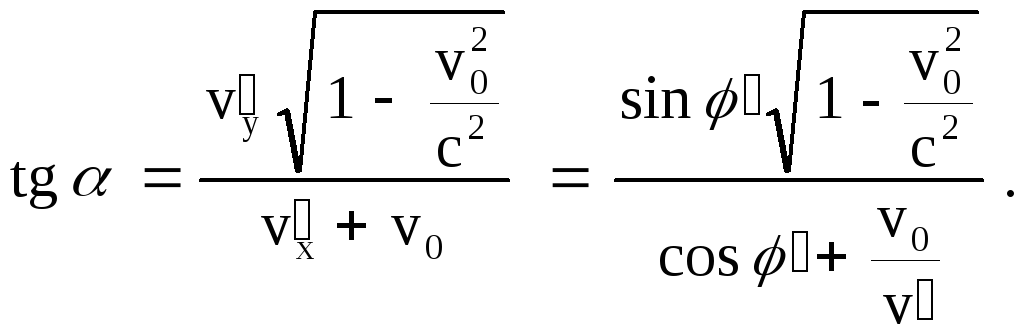
Сделаем вычисления:

Ответ: = 34о, = 12о.
Пример 3. Частица с массой покоя m0, летящая со скоростью v1 = 0,8с, испытывает неупругое соударение с идентичной покоящейся частицей. Найти массу покоя m0, скорость v и кинетическую энергию Eк частицы, образовавшейся в результате удара.
Р ешение
ешение
Поскольку скорость налетающей частицы близка к скорости света, задачу следует решать в рамках релятивистской динамики. Неупругость удара, оговоренная в условии, означает, что после удара частицы движутся вместе, образовав некоторую новую частицу с массой покоя m0. Конкретные условия удара (направление вектора v1, наличие других тел, с которыми возможно взаимодействие) не оговорены в условии. Поэтому решение возможно только в предположении, что соударяющиеся частицы образуют замкнутую систему тел. В этом случае импульс системы и ее полная энергия остаются постоянными.
![]() .
.
Индексы 1 и 2 обозначают состояние системы до и после соударения.
Учитывая, что до удара система состоит из двух одинаковых частиц, одна из которых покоится, запишем импульс и полную энергию системы в начальном состоянии:
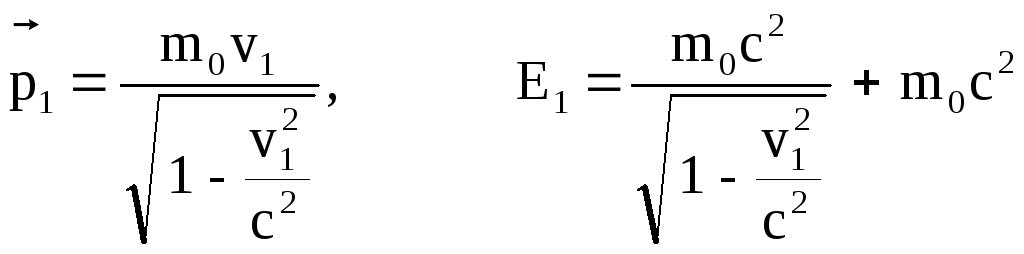 .
.
После взаимодействия система состоит из одной частицы, масса покоя которой m0 и скорость v.
Тогда
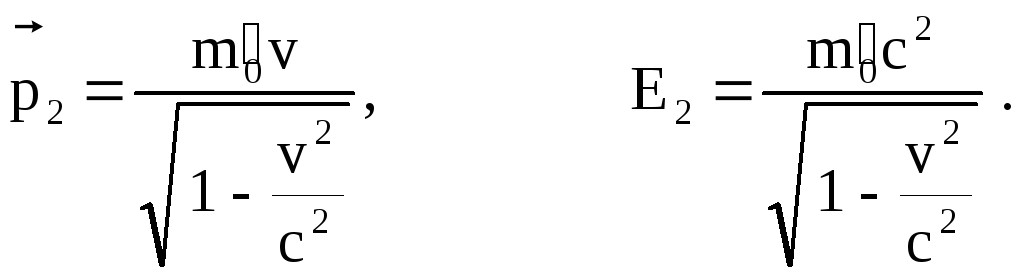
Из последней пары формул, записав предварительно выражение для модуля импульса p2, легко получить:
![]() .
.
Используя законы сохранения, находим:
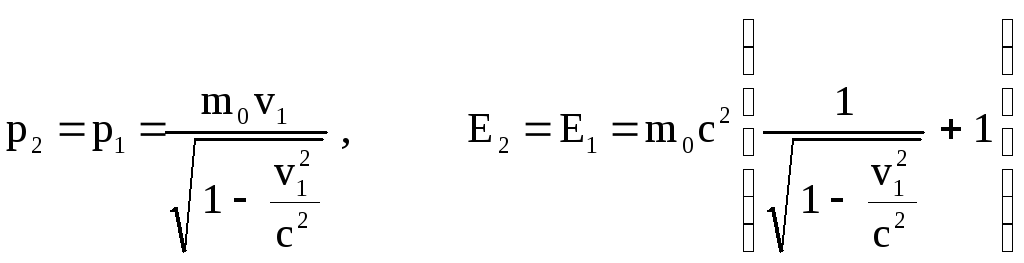
Подставляя в последние формулы условие v1 = 0,8с, получим:
![]()
Теперь, подставляя полученные значения p2 и Е2 в выражение для скорости v, получаем:
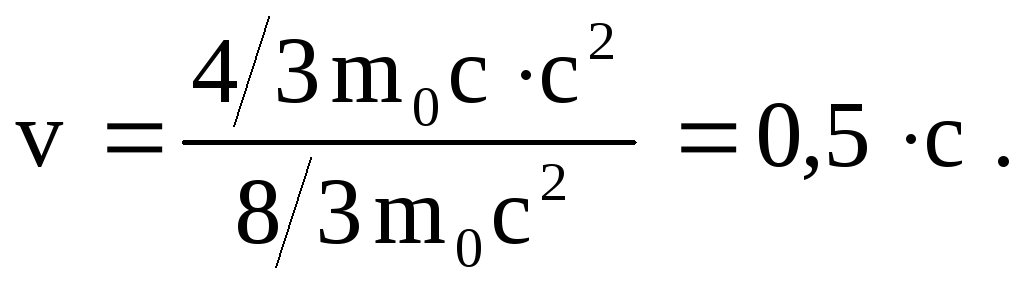
Используем связь между энергией и импульсом частицы в релятивистской динамике:
![]() .
.
Запишем это выражение для второго (после удара) состояния системы и выразим из него m0.
![]()
Подставляя в последнее выражение значения для p2 и Е2, получим:
![]()
Как видно, масса покоя образовавшейся частицы больше, чем сумма масс покоя частиц, составлявших систему до соударения.
Наконец найдем кинетическую энергию образовавшейся частицы, используя общее выражение для кинетической энергии в релятивистской динамике:
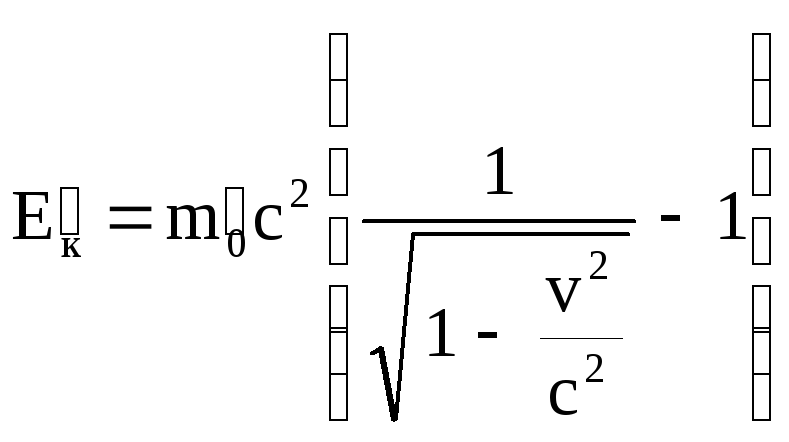 .
.
Подставляя сюда m0 = 2,31 m0, и v = 0,5 c, получим Ек = 0,36 m0c2.
Ответ: m0 = 2,31 m0, v = 0,5c, Ек = 0,36 m0c2.
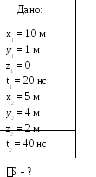 Пример
4. Два события
произошли в системе отсчета К в мировых
точках с координатами x1
= 10 м; y1
= 1 м; z1
= 0; t1
= 20 нс и x2
= 5 м; y2
= 4 м; z2
= 2 м; t2
= 40 нс. Можно ли найти систему отсчета в
которой оба события происходят: 1) в
одной точке пространства; 2) в один
момент времени? Могут ли эти события
быть причинно связаны друг с другом?
Пример
4. Два события
произошли в системе отсчета К в мировых
точках с координатами x1
= 10 м; y1
= 1 м; z1
= 0; t1
= 20 нс и x2
= 5 м; y2
= 4 м; z2
= 2 м; t2
= 40 нс. Можно ли найти систему отсчета в
которой оба события происходят: 1) в
одной точке пространства; 2) в один
момент времени? Могут ли эти события
быть причинно связаны друг с другом?
Решение
Для того, чтобы ответить на поставленные вопросы, достаточно найти величину, которая называется интервалом между двумя событиями.
![]() .
.
Рассчитаем интервал для событий, о которых говорится в условии:
![]()
Как видим, интервал получился мнимым. Такие интервалы называются пространственноподобными. События, разделенные таким интервалом, являются абсолютно удаленными, они всегда разделены в пространстве, то есть невозможно найти систему отсчета, в которой оба события происходят в одной точке. В то же время последовательность таких событий в разных системах отсчета может быть различной. Имеется одна система отсчета, в которой эти события происходят одновременно. Абсолютно удаленные события не могут быть причинно связаны друг с другом, так как находятся на большем расстоянии друг от друга, чем расстояние, которое может пройти свет за промежуток времени между этими событиями. Таким образом, их взаимное влияние совершенно невозможно.
Ответ: 1) нельзя; 2) да, можно; 3) нет, не могут.
