
- •Министерство образования и науки российской федерации
- •Матрицы. Определители
- •Кривые второго порядка.
- •Плоскость.
- •Прямая в пространстве.
- •Прямая и плоскость в пространстве.
- •Табличное интегрирование
- •Типовой расчет № 1
- •Типовой расчет № 2
- •1. Написать каноническое уравнение прямой
- •Типовой расчет № 3
- •Список рекомендуемой литературы
Табличное интегрирование
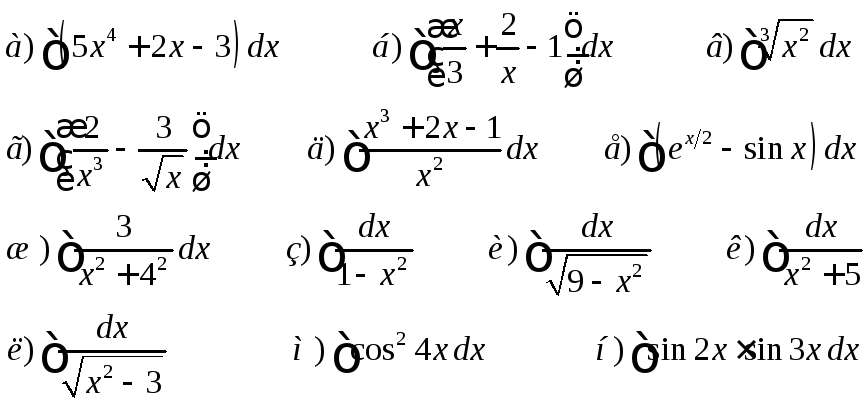
Метод подстановки
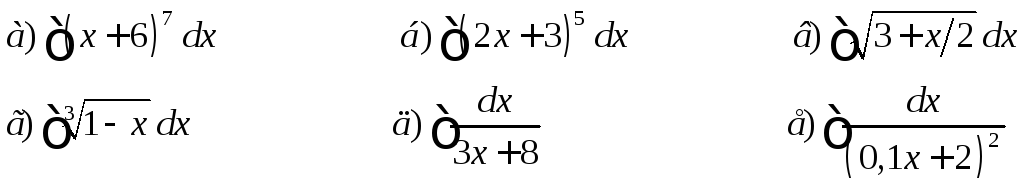
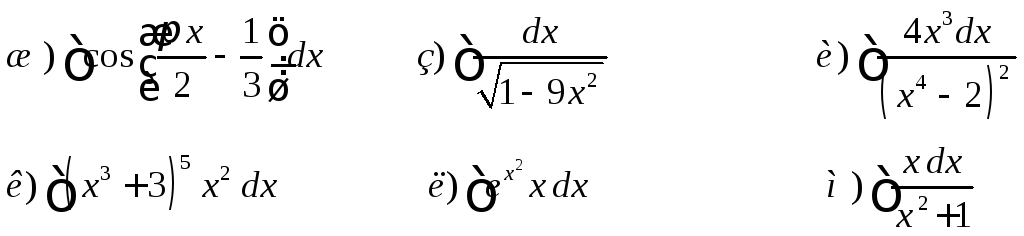
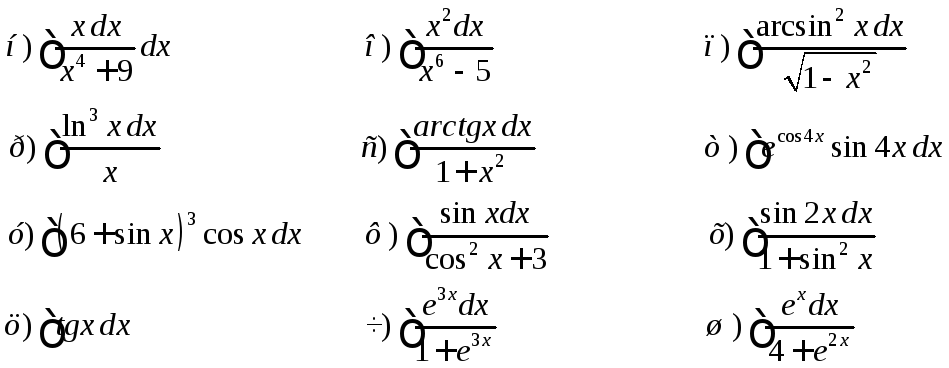
Дома.
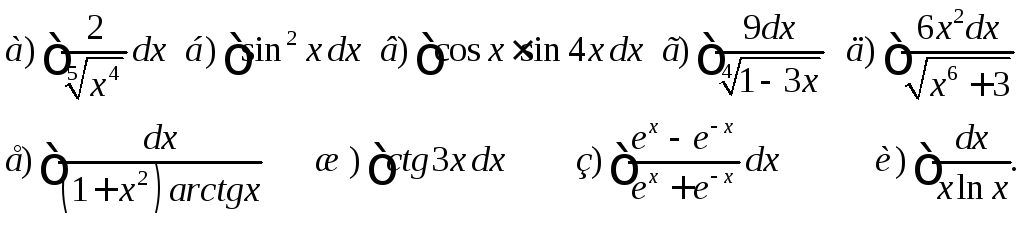
Ответы:
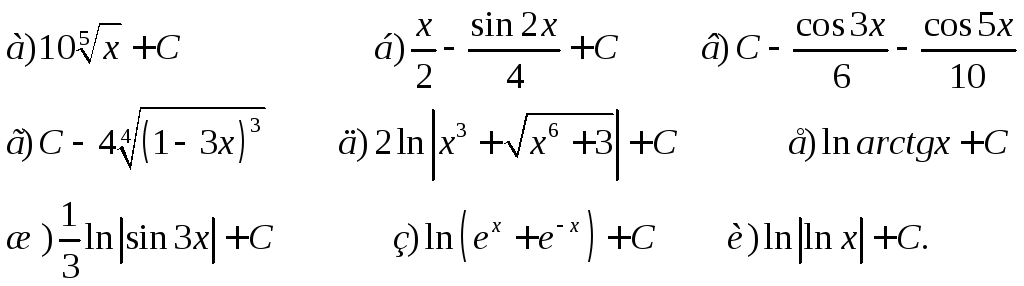
Интегрирование по частям
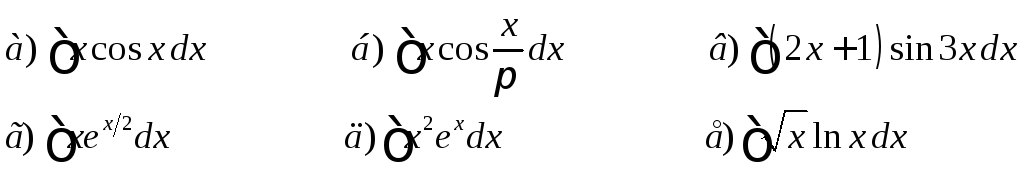
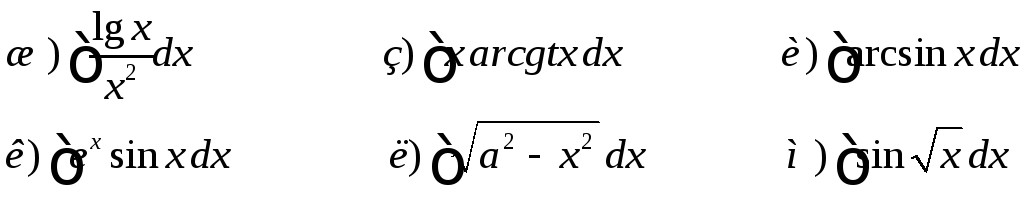
Дома.
![]() .
.
Ответы:
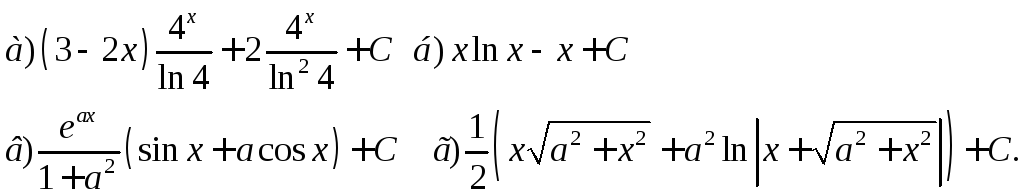
Интегрирование рациональных дробей
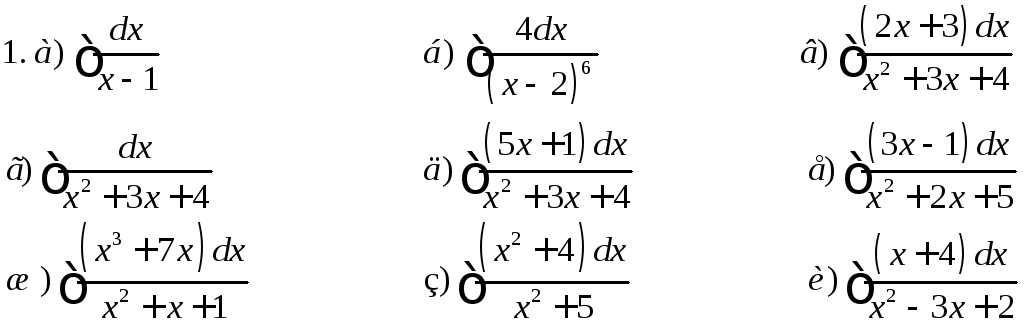
2. Представить правильные дроби в виде суммы простейших дробей

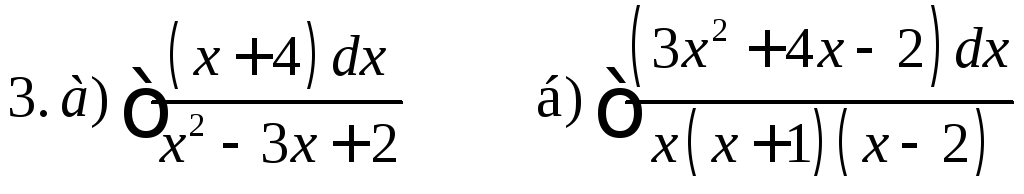
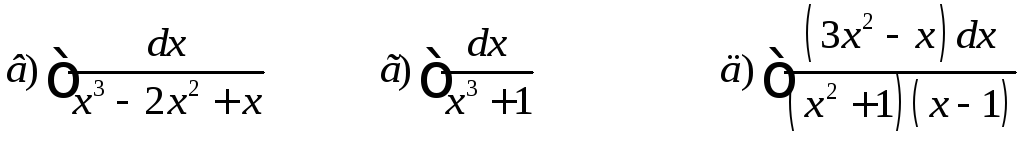
Дома.
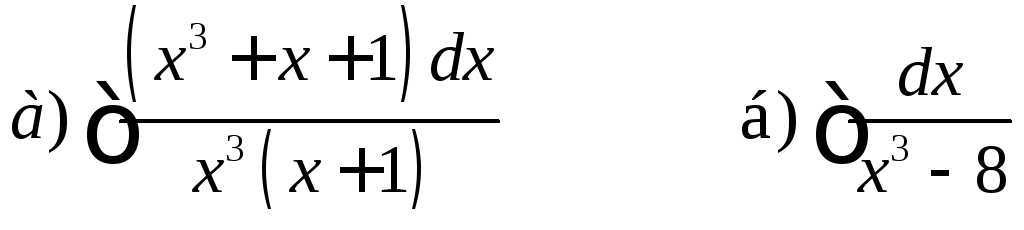
Ответы:
![]()
![]()
Интегрирование некоторых иррациональных функций
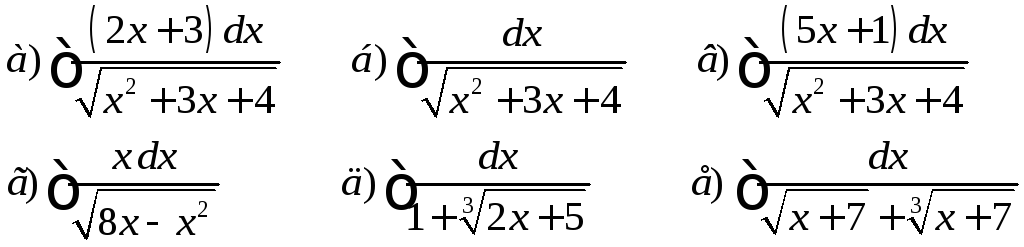
Дома
![]()
Ответы:
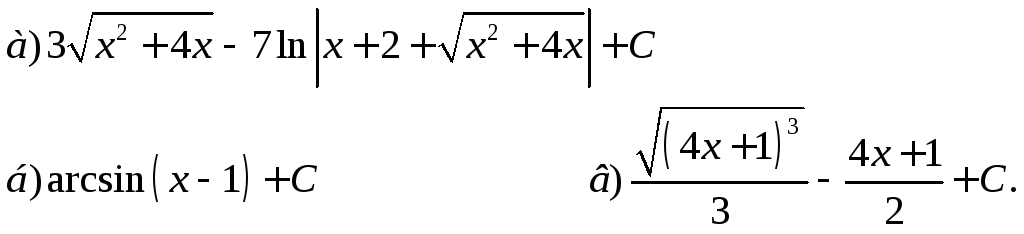
Интегрирование тригонометрических функций
![]()
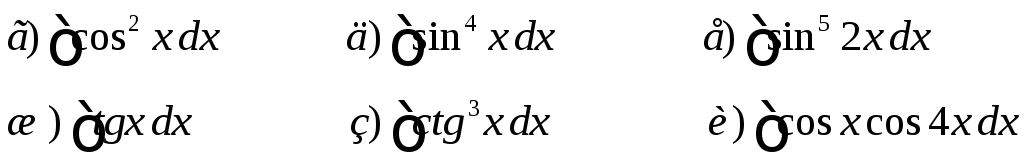
Дома.
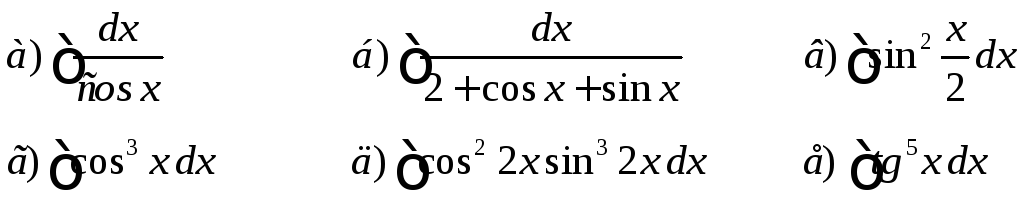
Ответы:
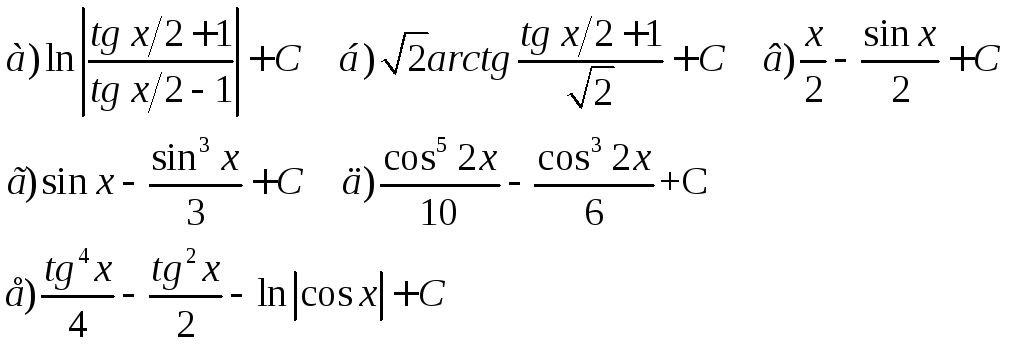
Разные интегралы
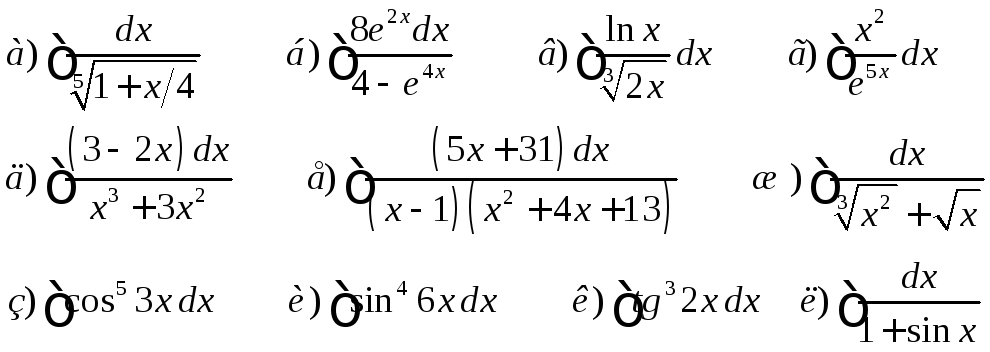
Ответы:
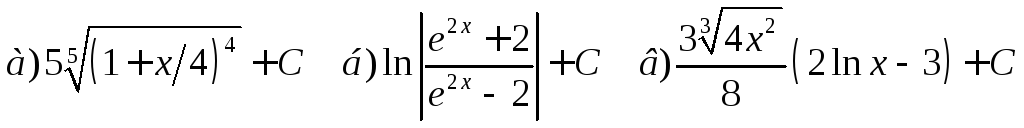
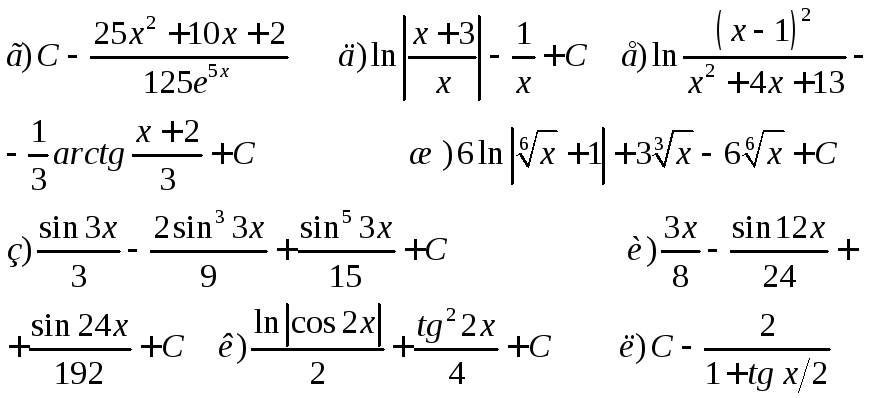
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1. Вычислить определенный интеграл
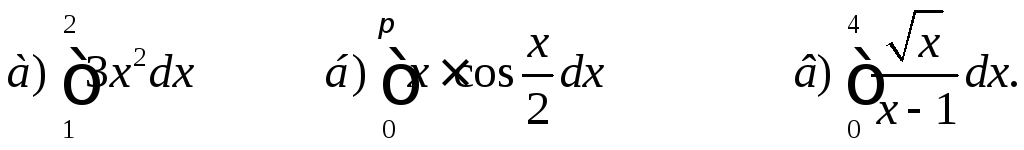
2. Найти площадь фигуры, ограниченной линиями
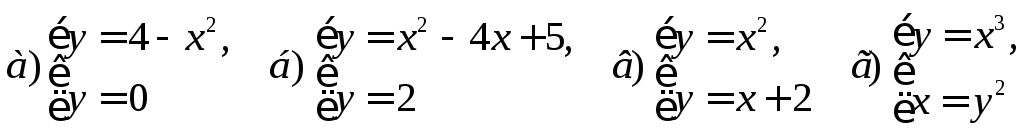 3.
Найти площадь фигуры, ограниченной
линиями
3.
Найти площадь фигуры, ограниченной
линиями
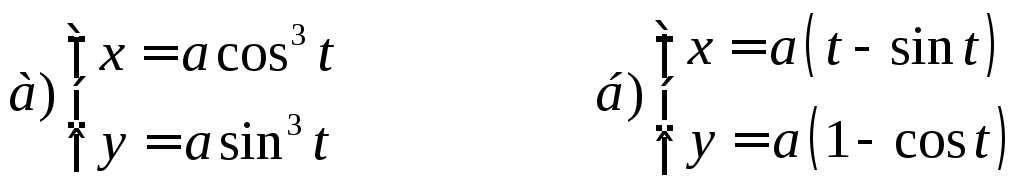
4. Найти площадь фигуры, ограниченной линиями
![]()
![]() .
.
5. Найти длину дуги
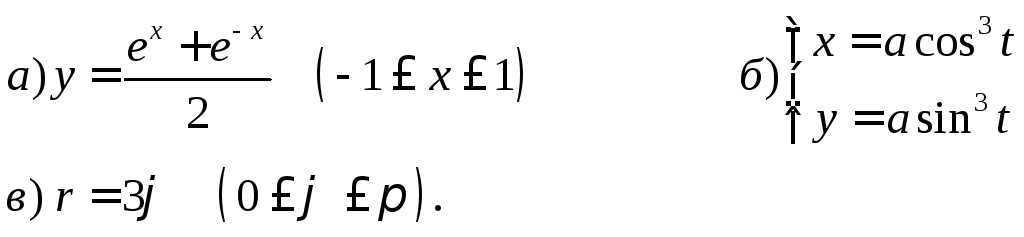
6. Найти объемы тел вращения вокруг координатных осей

7. Найти момент
инерции относительно оси
![]() однородного
(
однородного
(![]() )
стержня, заданного уравнением
)
стержня, заданного уравнением
![]()
![]()
8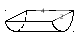 .
а) Найти работу по выкачиванию жидкости
плотности
.
а) Найти работу по выкачиванию жидкости
плотности![]() из корыта, имеющего форму полуцилиндра
указанных на рисунке размеров.
из корыта, имеющего форму полуцилиндра
указанных на рисунке размеров.
б) Найти работу по
растягиванию пружины с коэффициентом
упругости
![]() на 20 см.
на 20 см.
9. Исследовать на сходимость несобственные интегралы
![]()
Дома.1. Найти площадь фигуры, ограниченной линиями
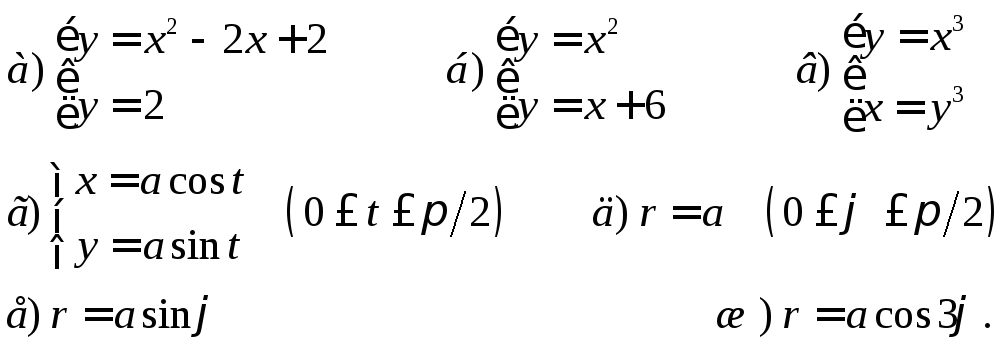
2. Найти длину дуги
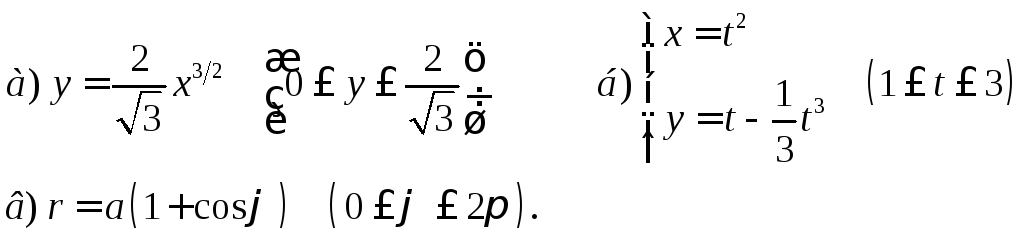
3. Найти объем
тела вращения вокруг оси![]() :
:![]()
![]() .
.
4. Найти моменты
инерции относительно координатных осей
однородного (![]() )
стержня, заданного уравнением
)
стержня, заданного уравнением![]() .
.
5. Найти работу
по выкачиванию жидкости плотности![]() из пирамиды с квадратным основанием
из пирамиды с квадратным основанием![]() высоты
высоты![]() .
.
6. Исследовать на сходимость несобственные интегралы
![]()
Ответы.
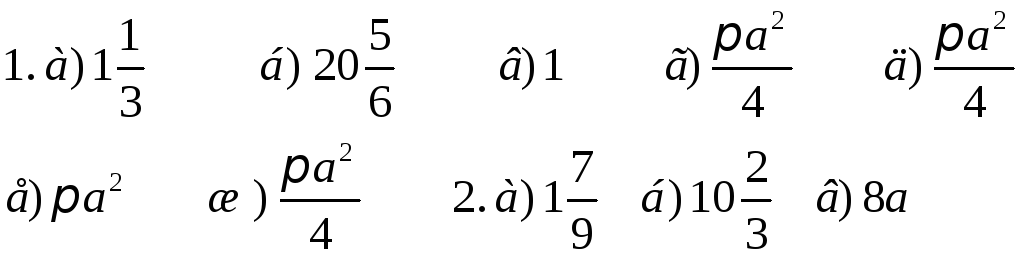
3.
![]() 4.
4.![]() 5.
5.![]()
6.
![]()
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
1. Решить ДУ с разделяющимися переменными
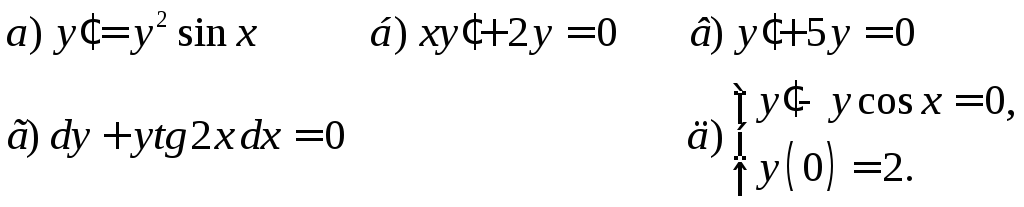
2. Решить однородное ДУ
![]()
3. Решить линейное ДУ
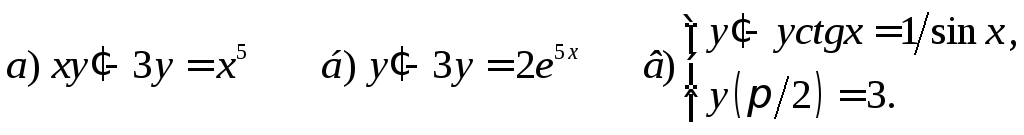
4. Решить уравнение Бернулли
![]()
5. Решить ДУ, допускающие понижение порядка
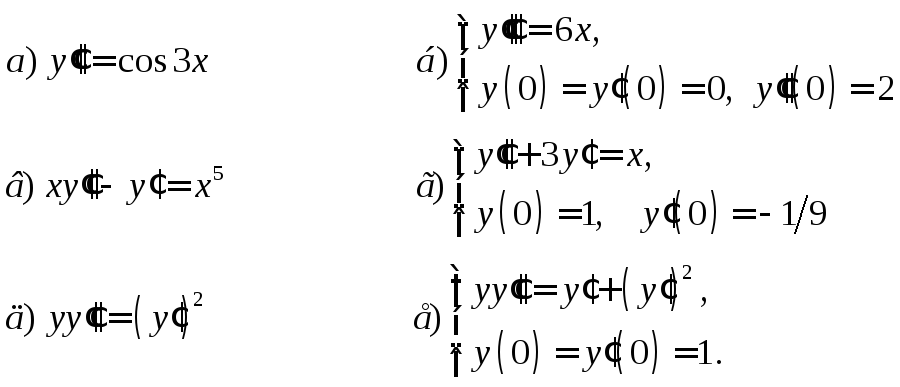
6. Решить однородное ДУ с постоянными коэффициентами
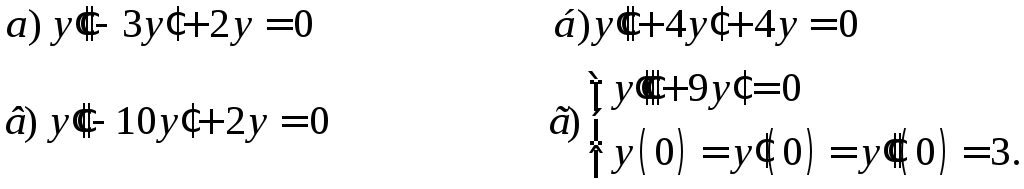
7. Решить ДУ второго порядка с постоянными коэффициентами с правой частью специального вида
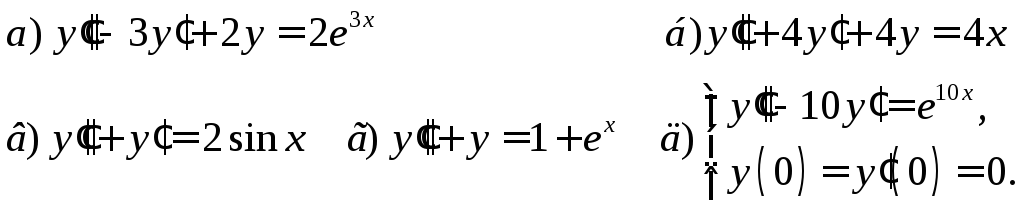
8. Решить ДУ второго порядка с постоянными коэффициентами методом вариации
![]()
9. Составить ДУ,
решением которого являлась бы функция
![]() .
.
10. Решить систему ДУ
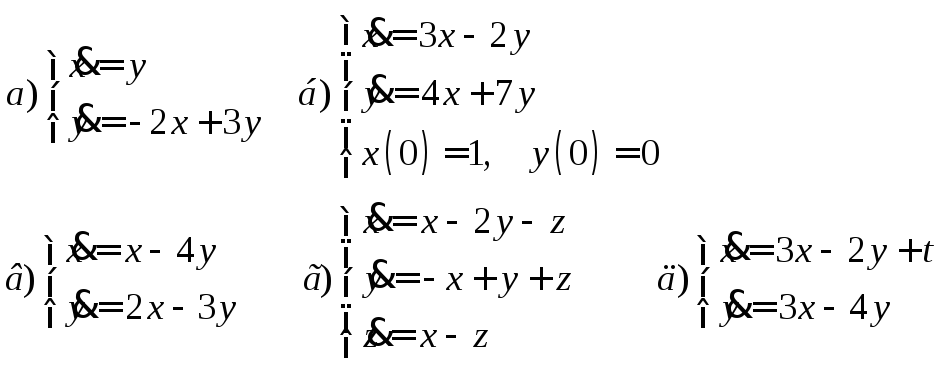
Дома.1. Решить ДУ первого порядка
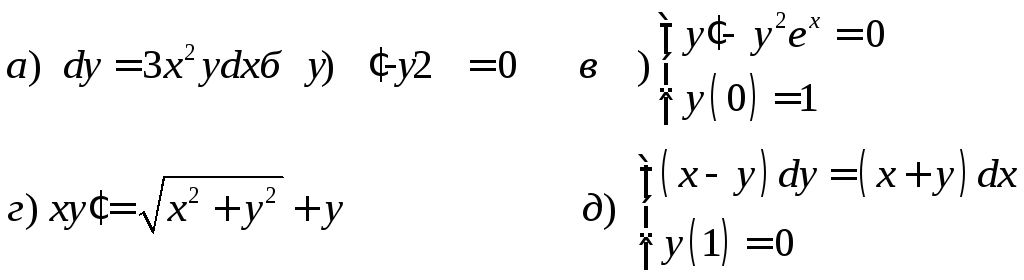

2. Решить ДУ, допускающие понижение порядка
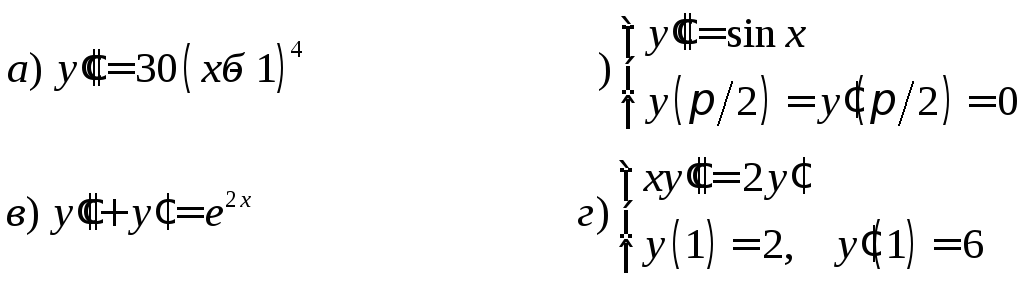
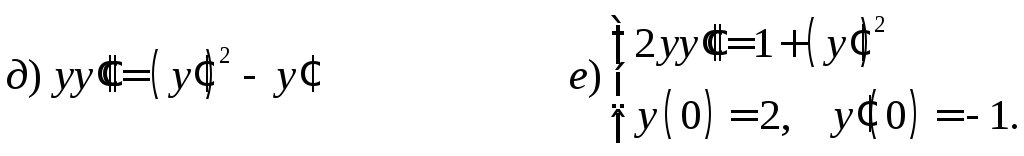
3. Решить ДУ второго порядка с постоянными коэффициентами
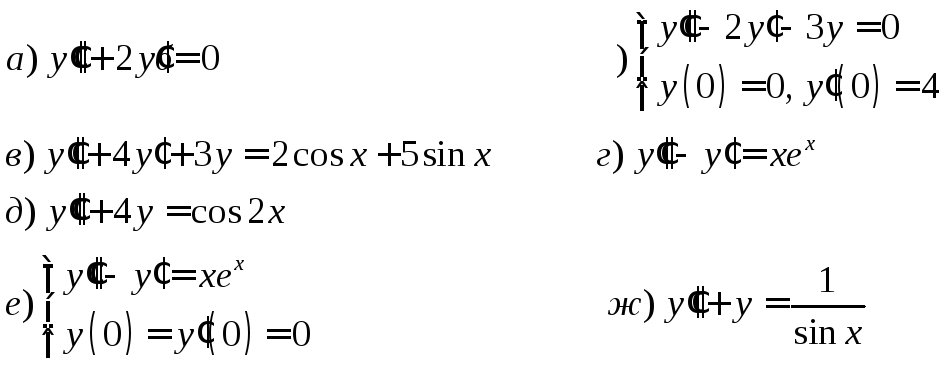
4. Решить систему ДУ
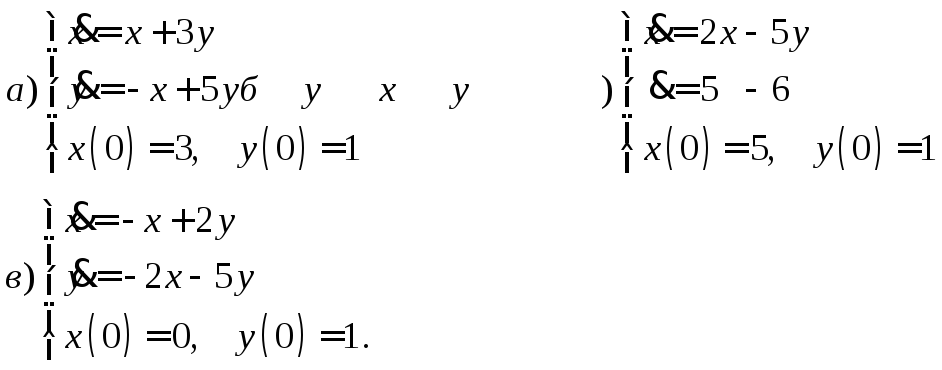
Ответы.
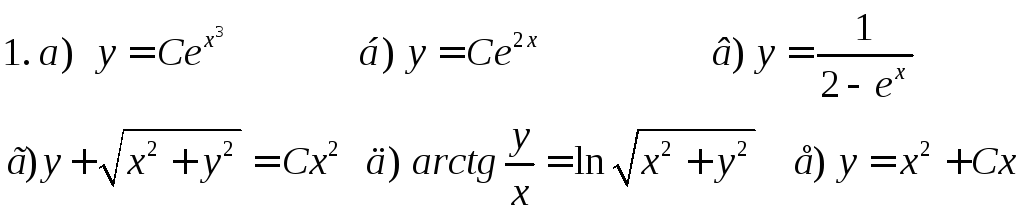
![]()
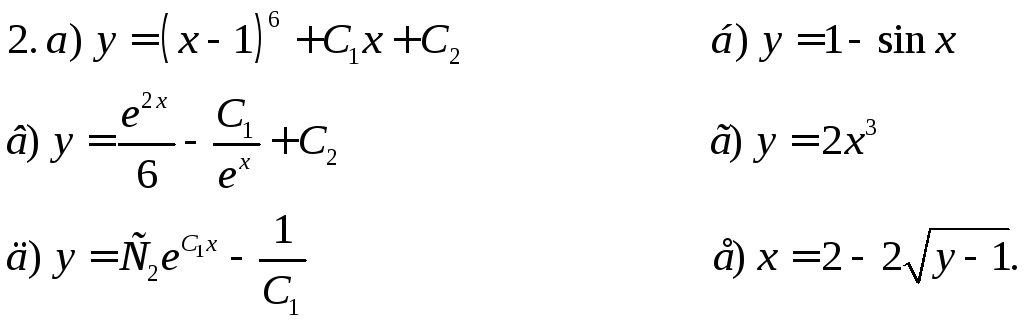
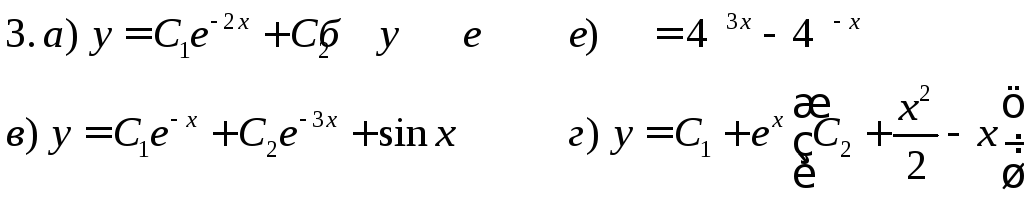
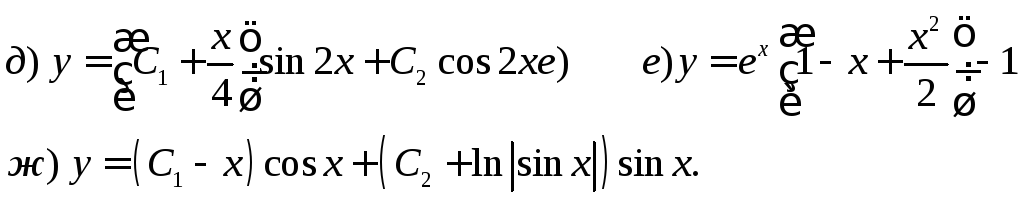
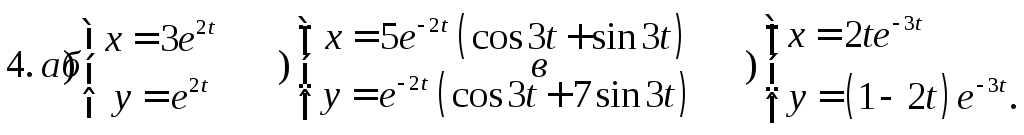
РЯДЫ
1. Написать первые
четыре члена ряда
![]() по заданному общему члену
по заданному общему члену![]() б)
б)![]() .
.
2. Найти формулу для общего члена ряда
![]() б)
б)
![]() .
.
3. Проверить
необходимое условие сходимости ряда
![]() :
:![]() б)
б)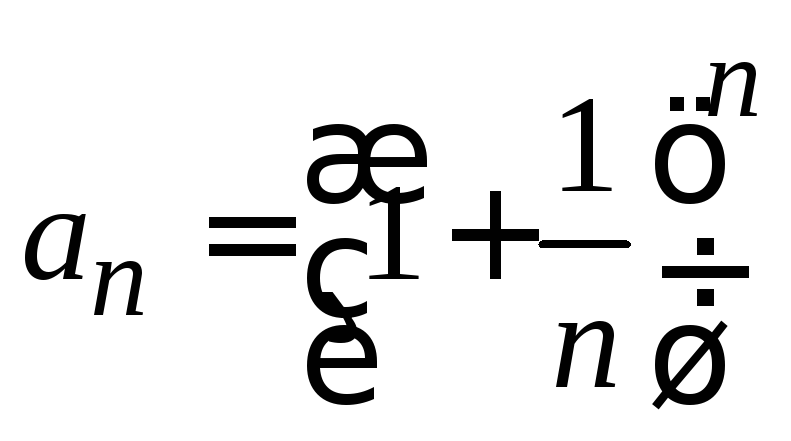 .
.
4. С помощью теорем сравнения исследовать ряд на сходимость
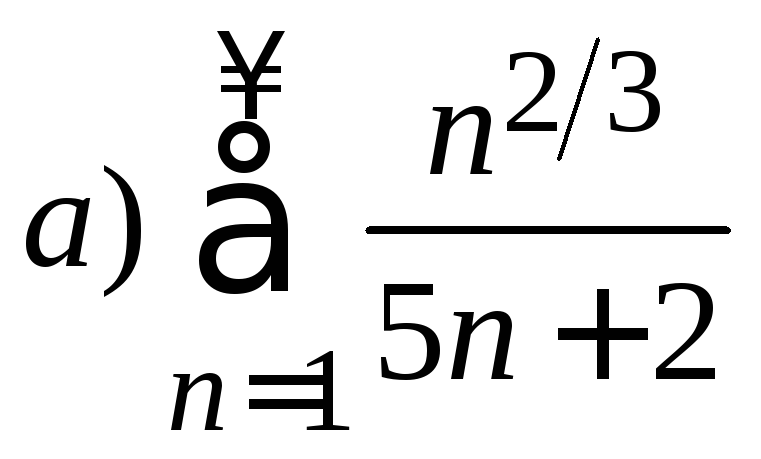 б)
б)
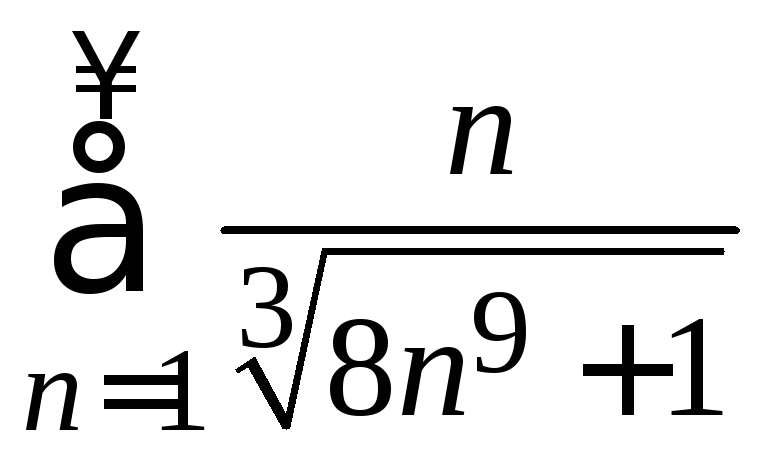 .
.
5. С помощью признака
Даламбера исследовать ряд на сходимость
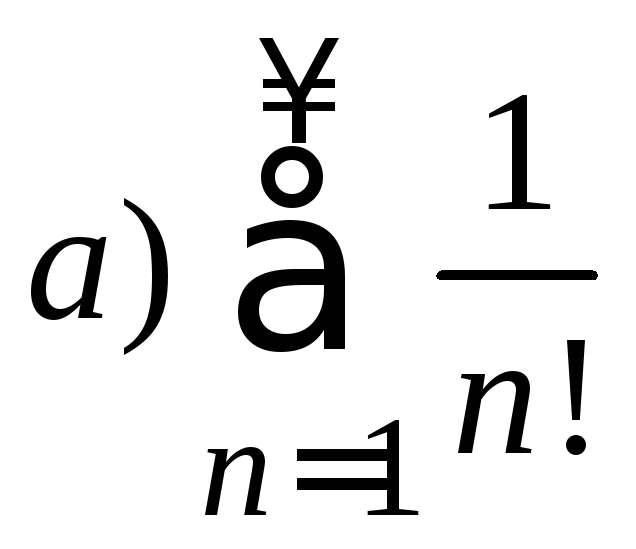 б)
б)![]() .
.
6. С помощью радикального признака Коши исследовать ряд на сходимость
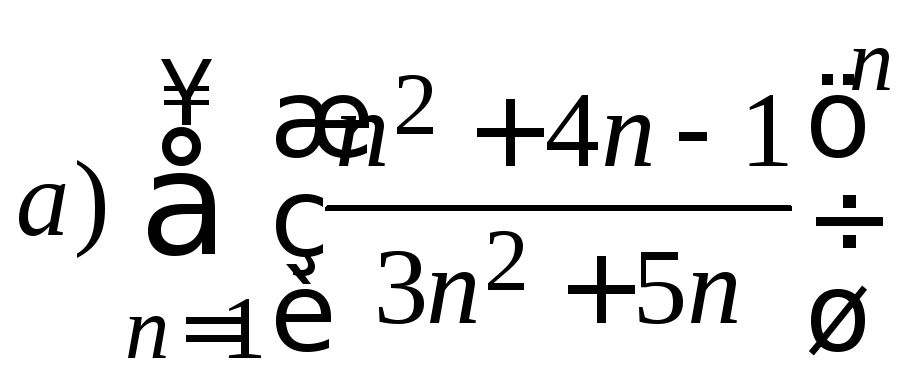 б)
б)
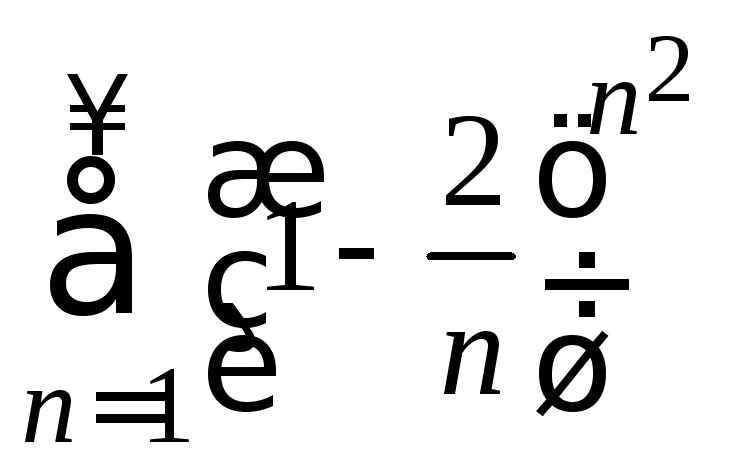 .
.
7. С помощью интегрального признака исследовать ряд на сходимость
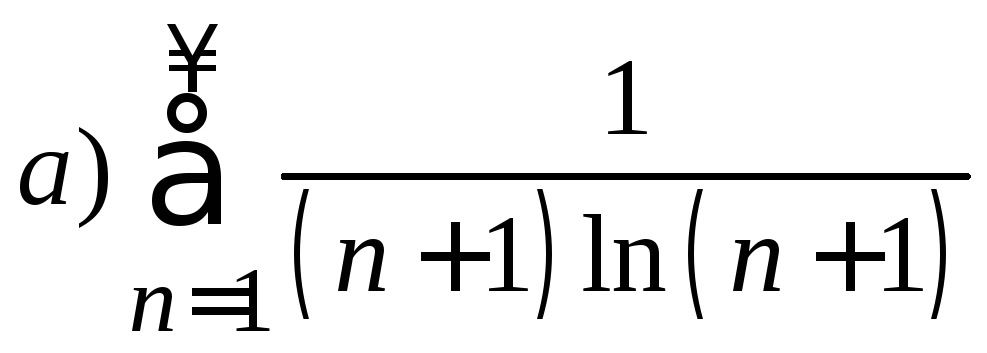 б)
б)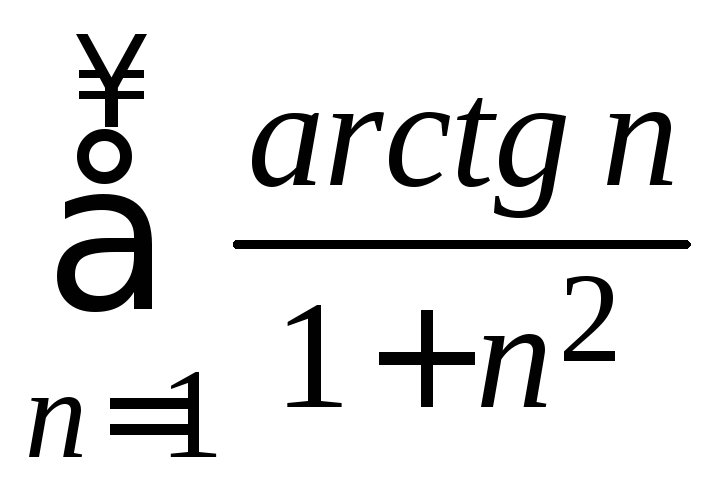 .
.
8. Исследовать на сходимость знакочередующийся ряд. В случае сходимости определить ее тип.
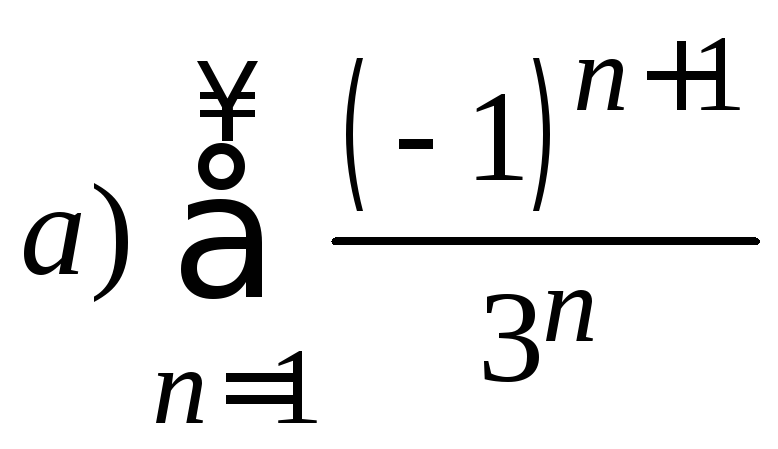 б)
б)
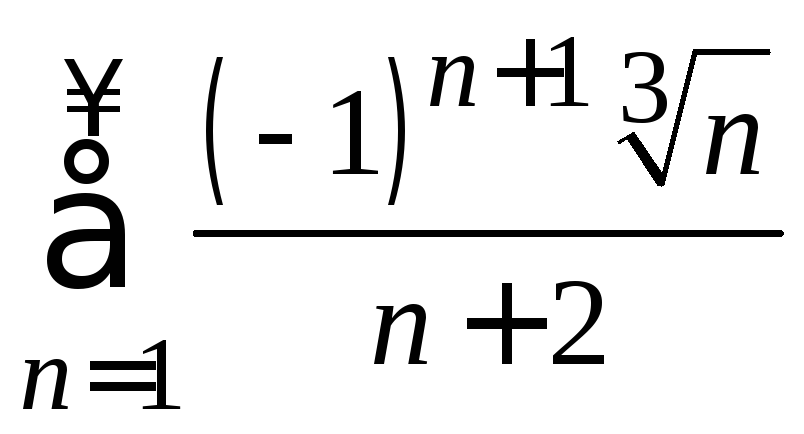 .
.
9. Найти область сходимости степенного ряда
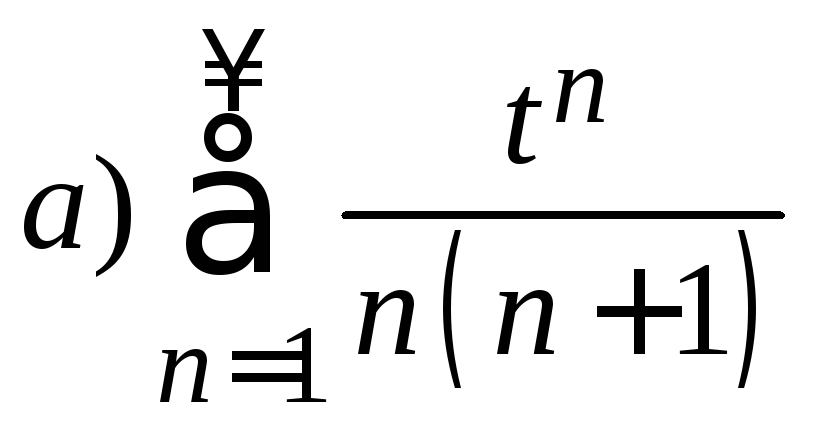 б)
б)
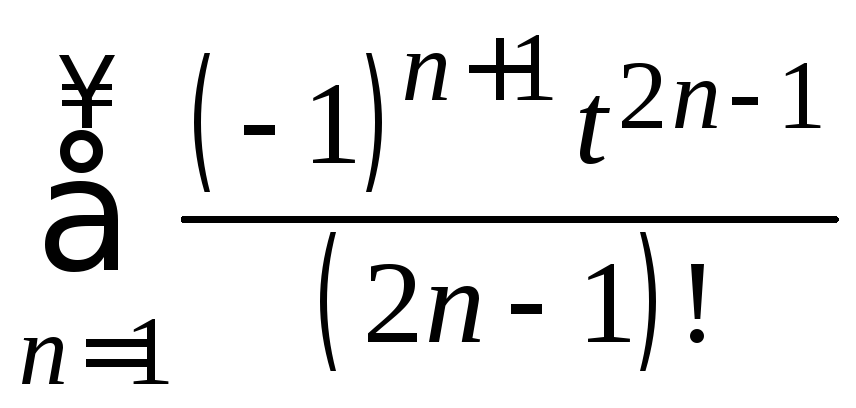
 .
.
10. Разложить функцию в степенной ряд и указать область его сходимости
![]() по степеням
по степеням
![]() б)
б)![]() по степеням
по степеням![]() .
.
11. Вычислить
приближенно с точностью
![]()
![]() б)
б)
![]() .
.
12. Решить приближенно задачу Коши
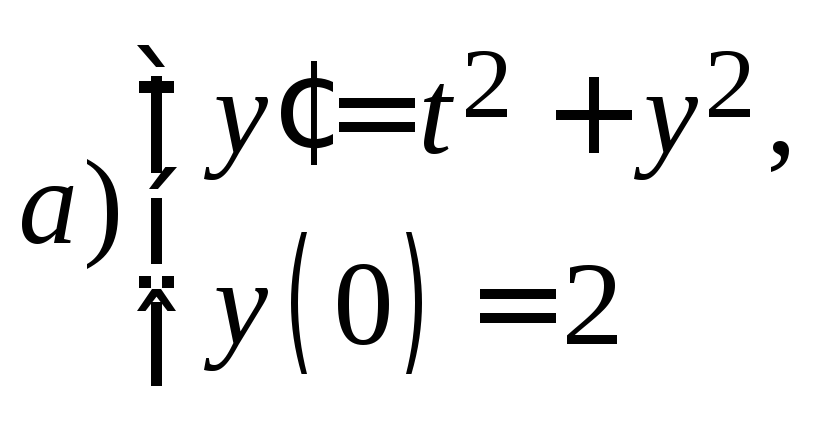 б)
б)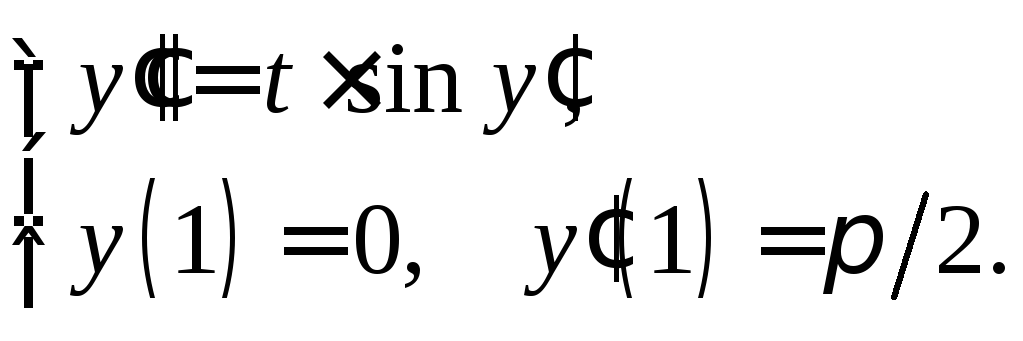
13. Исследовать комплексный ряд на сходимость
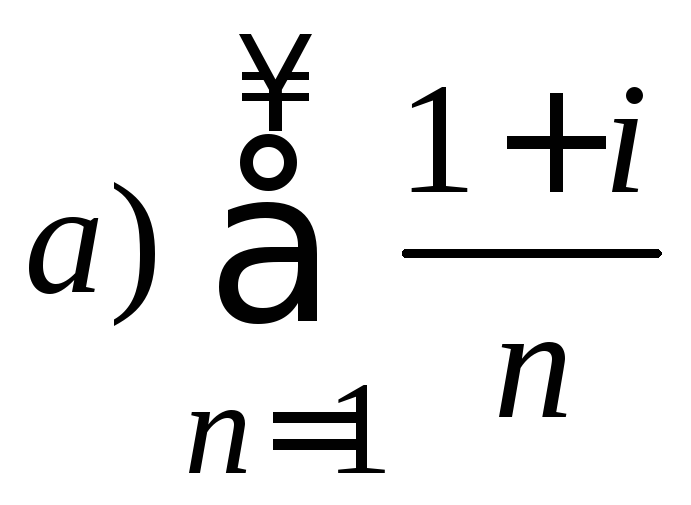 б)
б)
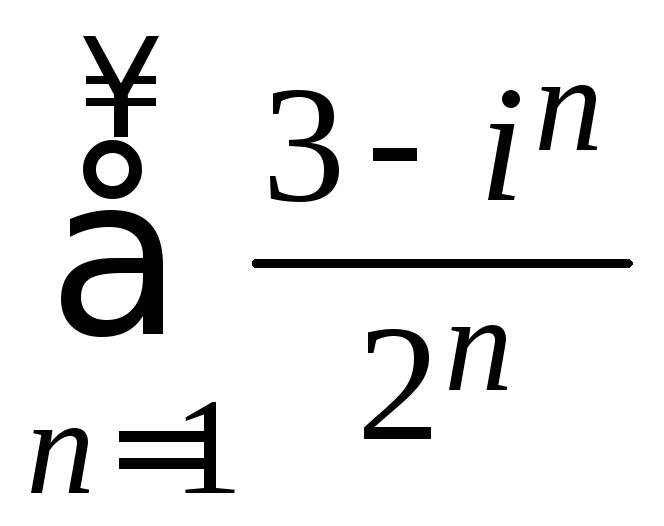 .
.
14. Найти область сходимости комплексного степенного ряда
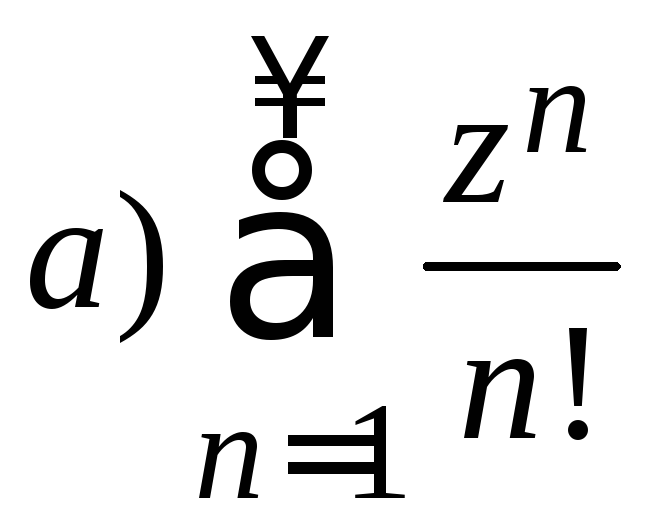 б)
б)
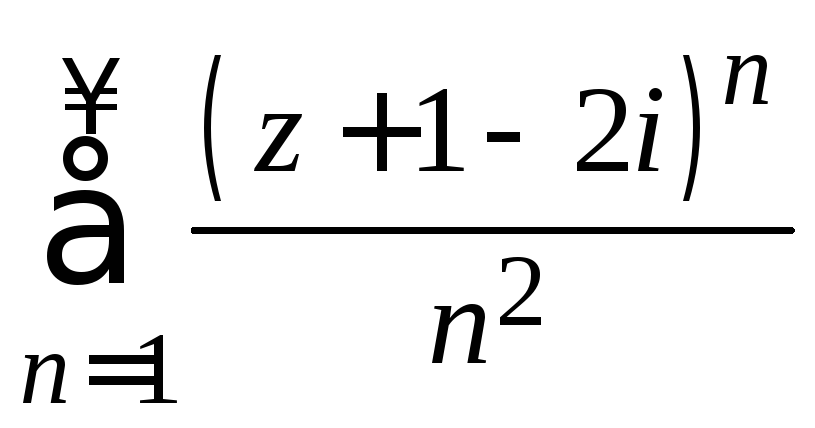 .
.
15. Разложить в тригонометрический ряд Фурье периодическую функцию
![]()
16. Разложить в ряд по косинусам функцию, заданную на полупериоде.
![]()
17. Представить в
комплексной форме гармоническое
колебание
![]() .
.
18. Разложить в
комплексный ряд Фурье периодическую
функцию
![]()
19. Представить интегралом Фурье в тригонометрической и комплексной форме функцию

и найти амплитуду ее гармонических составляющих.
Дома:
1. Исследовать ряд на сходимость
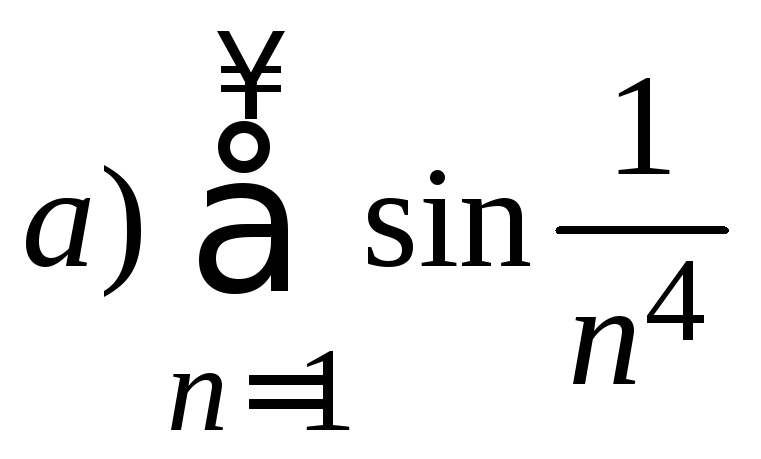
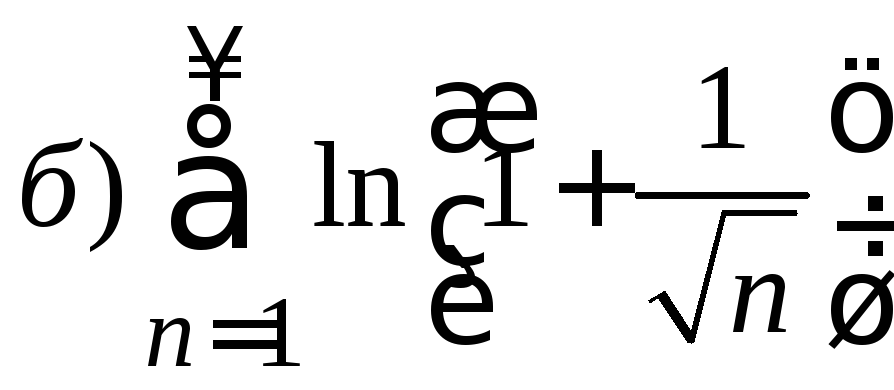
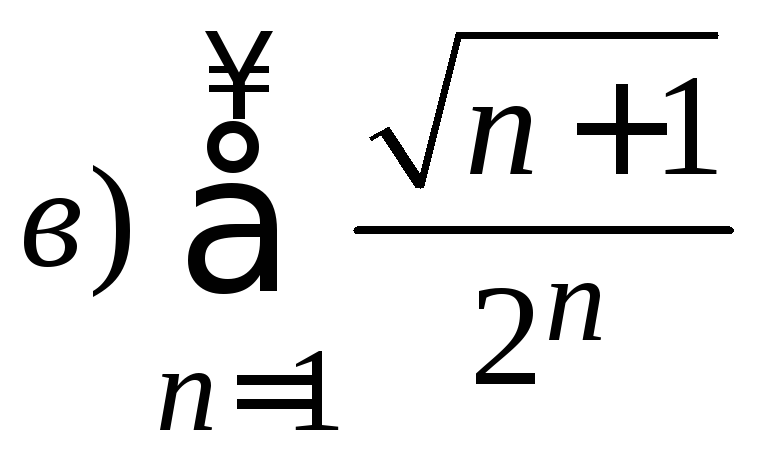
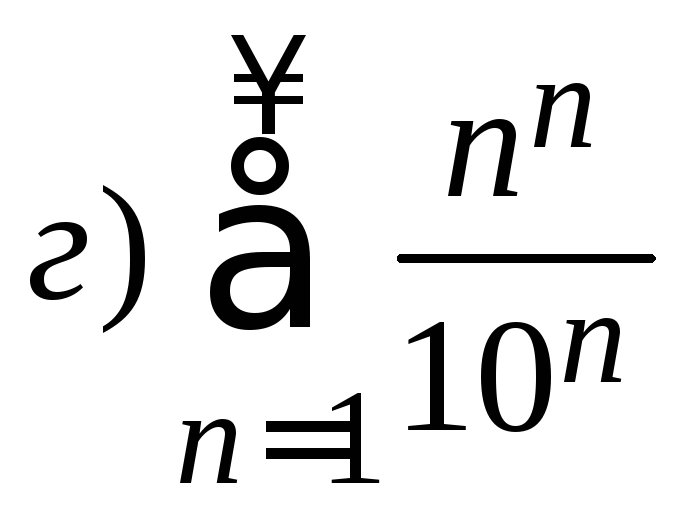
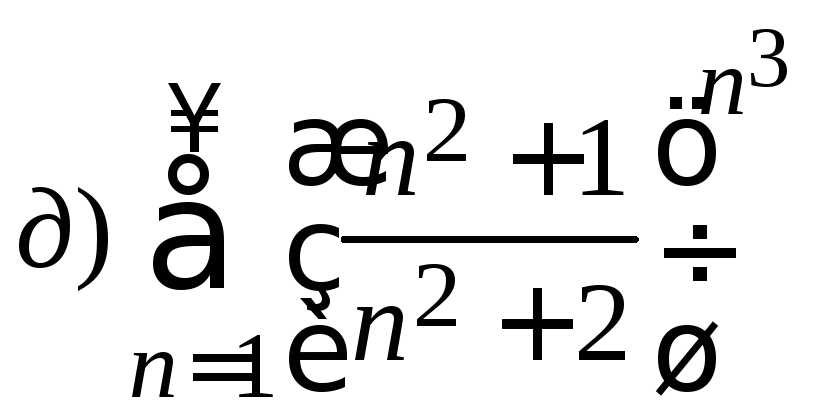
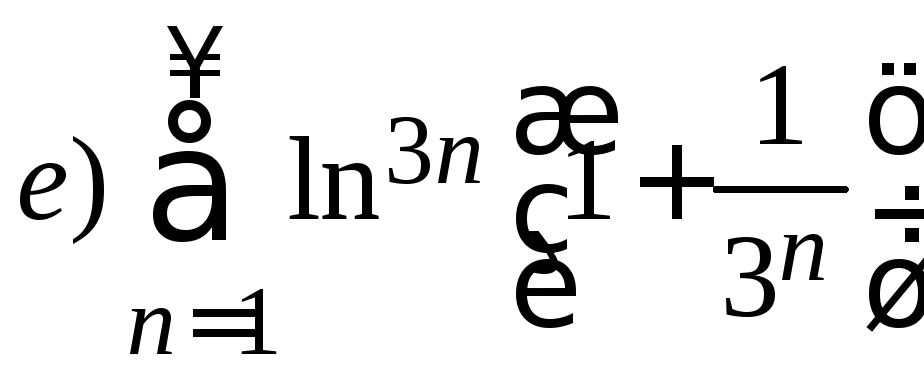
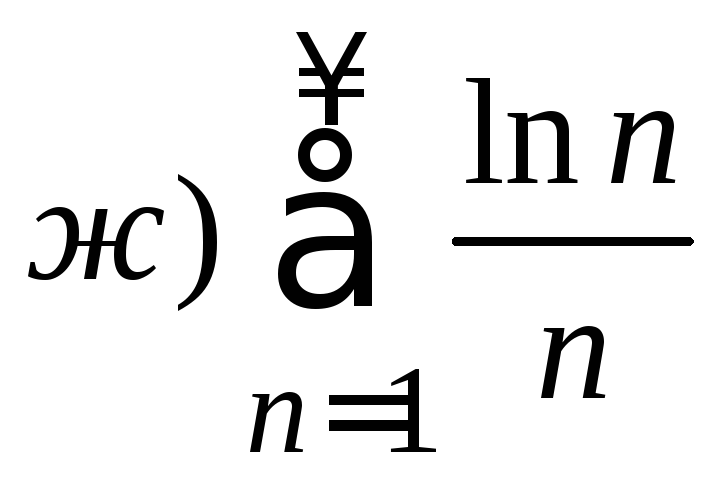
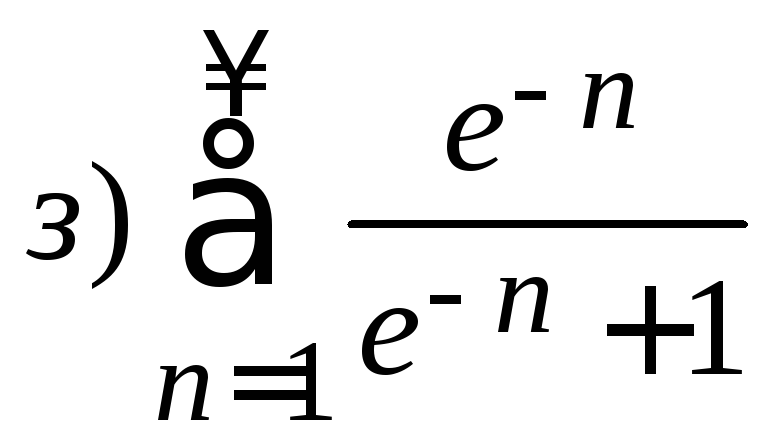 .
.
2. Исследовать на сходимость знакочередующийся ряд. В случае сходимости определить ее тип.
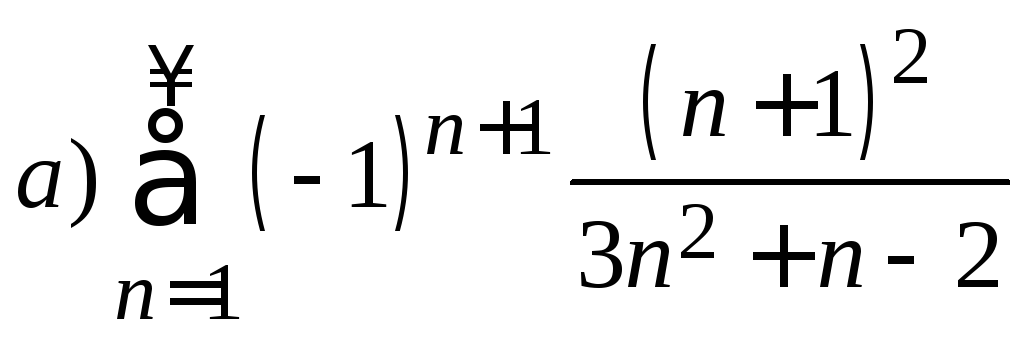
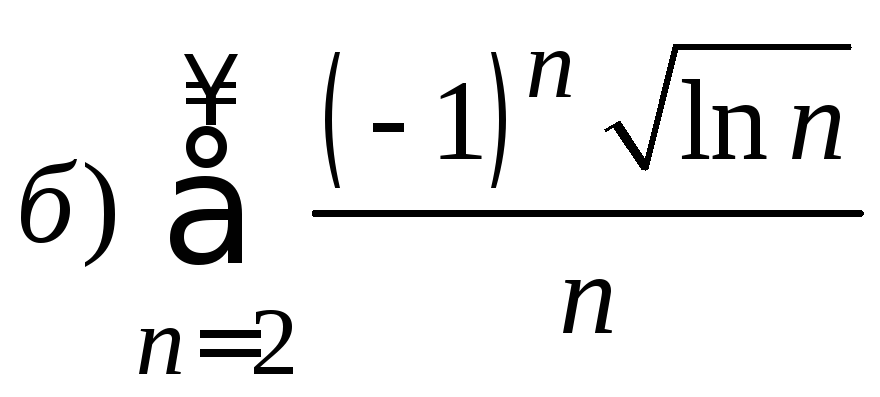 .
.
3. Найти область
сходимости степенного ряда
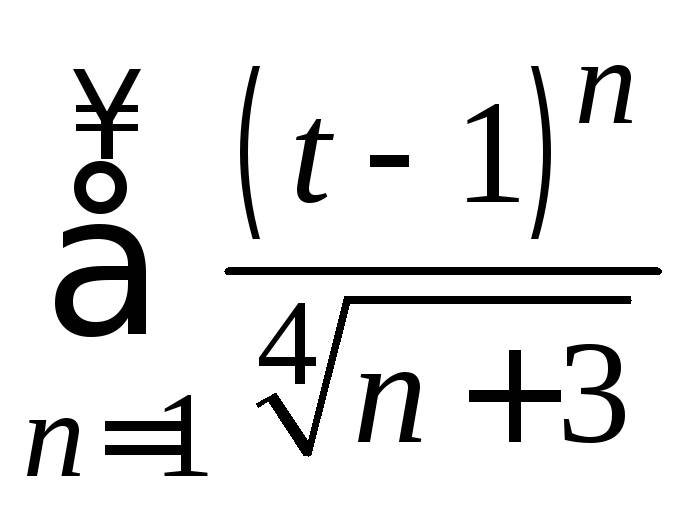 .
.
4. Разложить функцию в степенной
![]() по степеням
по степеням
![]()
![]() по степеням
по степеням![]() .
.
5. Вычислить с
точностью
![]()
![]()
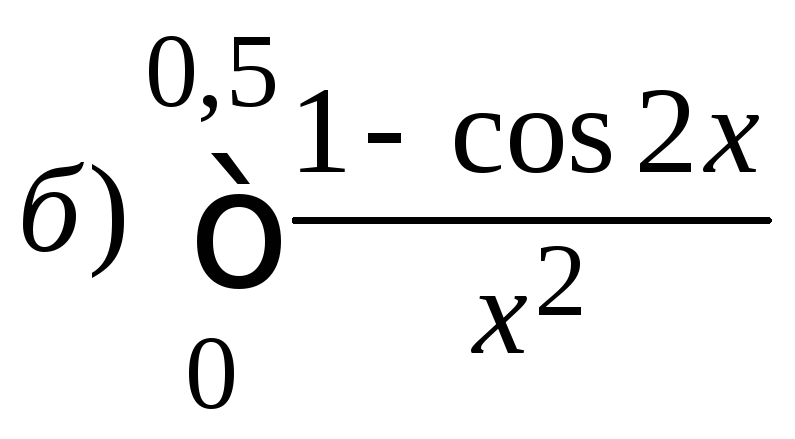 .
.
6. Решить приближенно задачу Коши
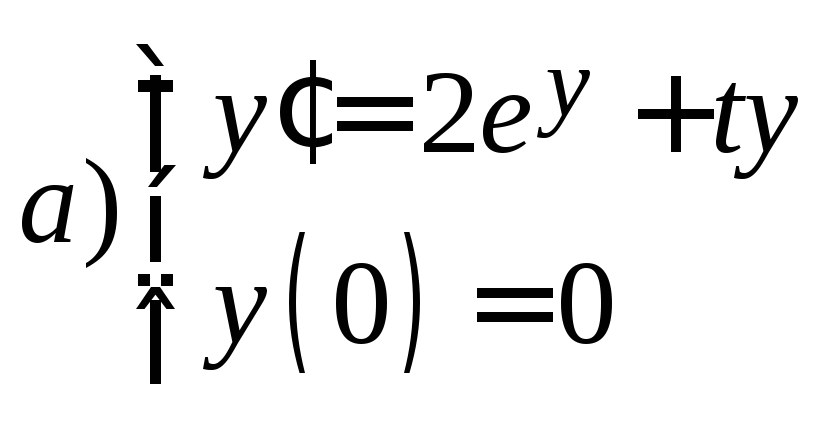
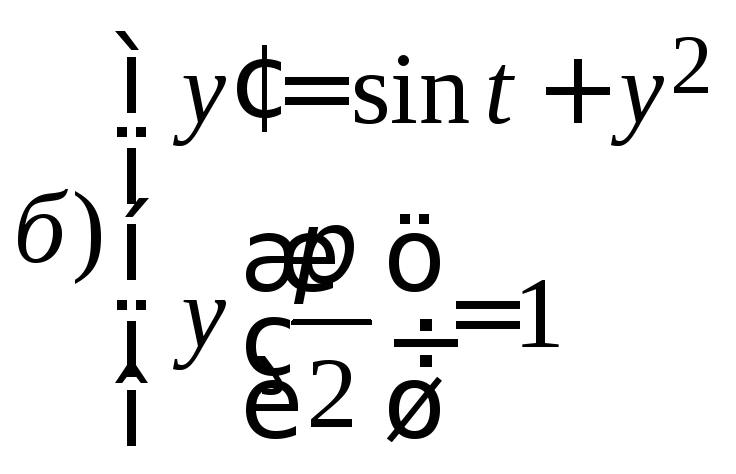
7.
Исследовать комплексный ряд на
сходимость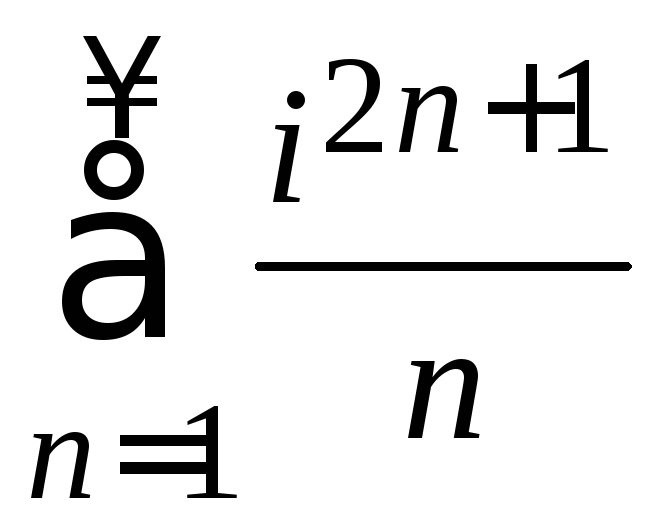 .
.
8. Разложить в тригонометрический ряд Фурье периодическую функцию
![]()
9. Разложить в ряд по синусам функцию, заданную на полупериоде
![]()
10. Разложить в тригонометрический и комплексный ряд Фурье функцию, заданную на отрезке:
![]() .
.
Ответы:
1. а) сходится; б)
расходится; в) сходится; г) расходится;
д) сходится; е) сходится ; ж) расходится;
з) сходится. 2. а) расходится; б)
сходится условно. 3.
![]() .
.
4.
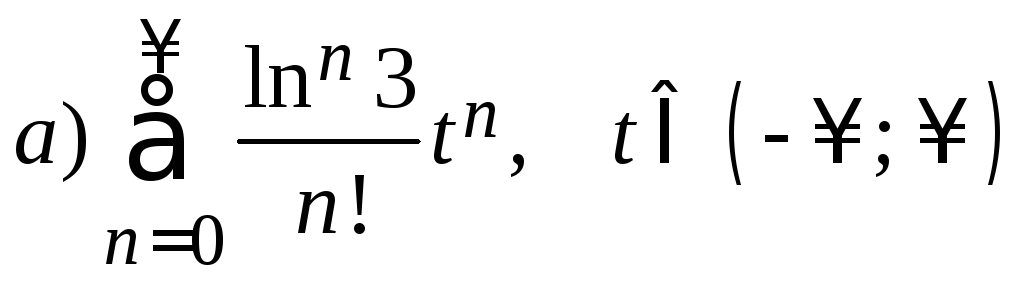
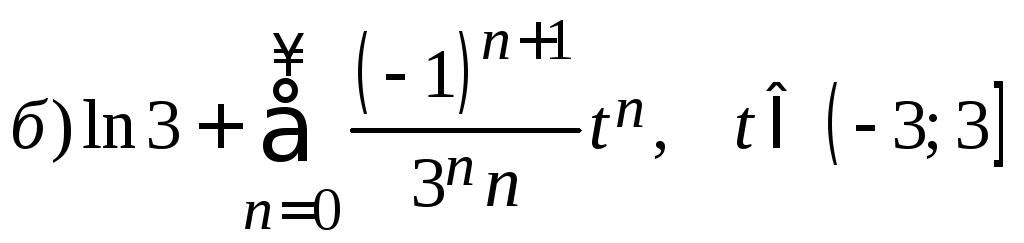 .
.
5.
![]()
![]() .
.
6.
![]() ;
;
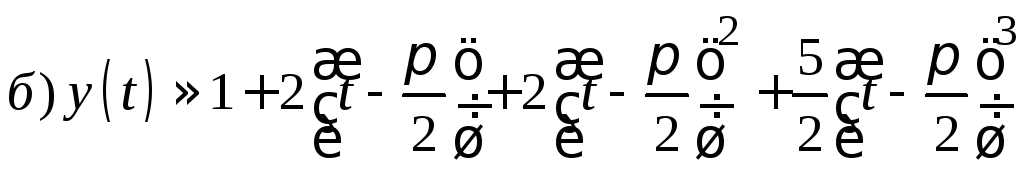 ;
;
7. Сходится условно.
8.
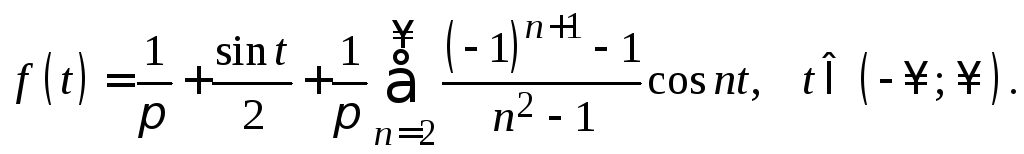
9.
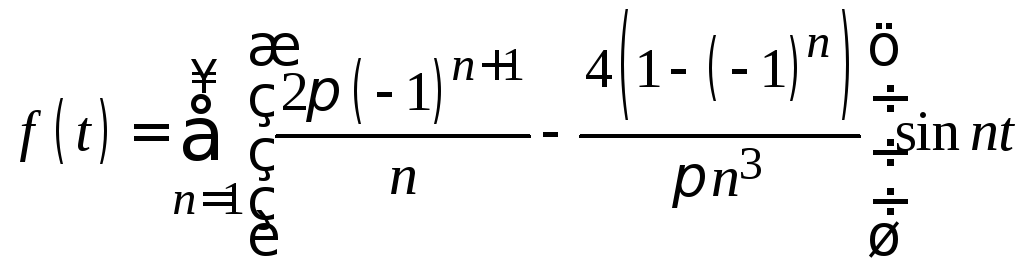 .
.
10.
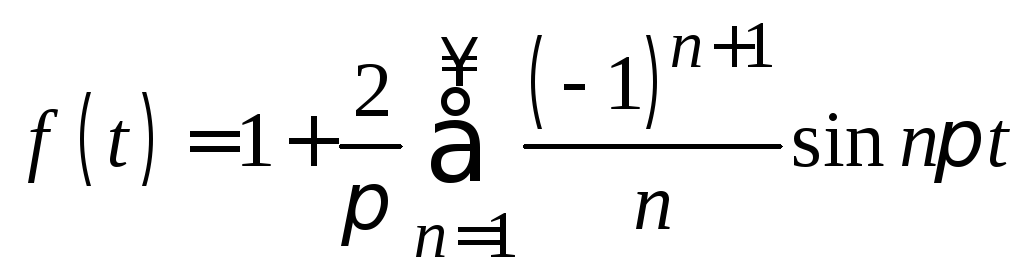 ,
,
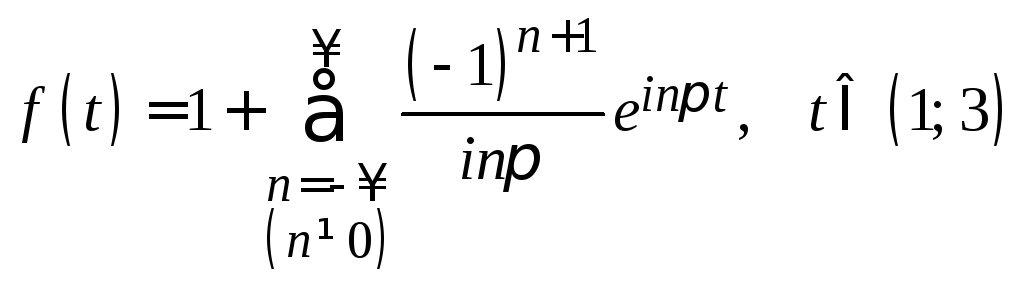 .
.
