Министерство образования и науки российской федерации

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

ОМСКИЙ ИНСТИТУТ (ФИЛИАЛ)

Е.Н. Стратилатова

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для решения задач

по дисциплине «Математика»

часть I

Омск

2008

УДК 51

ББК

С

Р е ц е н з е н т ы

Воробьева Е.В., кандидат физико-математических наук, доцент ОмГТУ;

Горощеня А.Б. кандидат физико-математических наук, доцент Омского института (филиала) РГТЭУ

Стратилатова, Елена Николаевна

Методические указания для решения задач по дисциплине «Математика». Часть I: Омск: Издатель ИП Погорелова, 2009.–60 с.

Методические указания предназначены для студентов 1 курса очной формы обучения всех специальностей при изучении следующих разделов: линейная и векторная алгебра, аналитическая геометрия, введение в анализ, дифференциальное и интегральное исчисления, дифференциальные уравнения, числовые и функциональные ряды. Методические указания содержат набор задач для решения на практических занятиях и при самоподготовке, а также задания для типовых расчетов по указанным разделам.

ISBN

Погорелова Е.В

© Стратилатова Е.Н © Омский институт

(филиал) РГТЭУ, 2008

ЛИНЕЙНАЯ АЛГЕБРА

Матрицы. Определители

1.Вычислить определители

2. Дано:

Выполнить действия:

3. Найти матрицы, обратные к данным

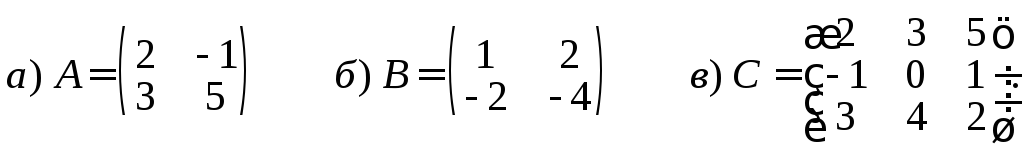
Дома.

1.Вычислить определители.

2. Дано:

Найти .

3. Найти матрицу, обратную к матрице

Ответы:

Системы линейных уравнений

1.Решить системы линейных уравнений по формулам Крамера

2. Решить СЛУ методом Гаусса

3. Решить СЛУ матричным методом

7. Найти матрицу .

Дома.

1.Решить СЛУ по формулам Крамера и матричным методом.

2. Решить СЛУ методом Гаусса.

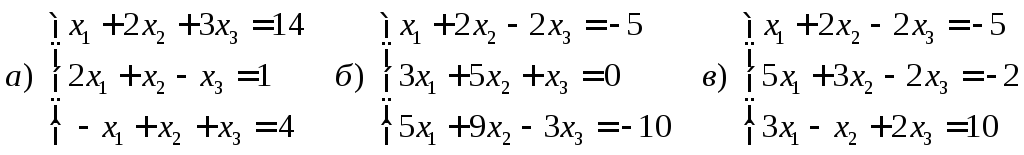
Ответы:

ВЕКТОРНАЯ АЛГЕБРА

Линейные операции над векторами

1. Доказать свойства:

2. В треугольнике ABCпостроить

3. В параллелепипеде . Построить

4. Коллинеарны ли векторы ?

5. Дано: . Найти разложение векторапо базису.

6. Даны две вершины параллелограмма: и точка пересечения его диагоналей. Определить две другие вершины.

7. Проверить, что – вершины трапеции.

Дома.

1. Даны последовательно координаты вершин параллелограмма:. Найти координаты вершины..

2. Точка О – центр масс треугольника АВС. Найти .

3. Дано: . Разложить векторпо базису.

Ответы:

Скалярное произведение.

1. Дано: . Вычислить:.

2. Дано: . Найти модуль вектора.

3. Вычислить работу, которую производит сила , когда ее точка приложения перемещается из начала в конец вектора.

4. Дано: . Вычислить проекцию векторана ось вектора.

5. Дано: . Найти:

а) длины сторон ; б) внутренние углы.

6. Найти модуль и направляющие косинусы вектора .

Дома.1. Дано:. Найти длину вектора.

2. Найти работу силы , если точка приложения, двигаясь прямолинейно, перемещается изв.

Ответы:

Векторное произведение.

1. Дано: . Вычислить:.

2. Дано: . Вычислить:.

3. Сила приложена к точке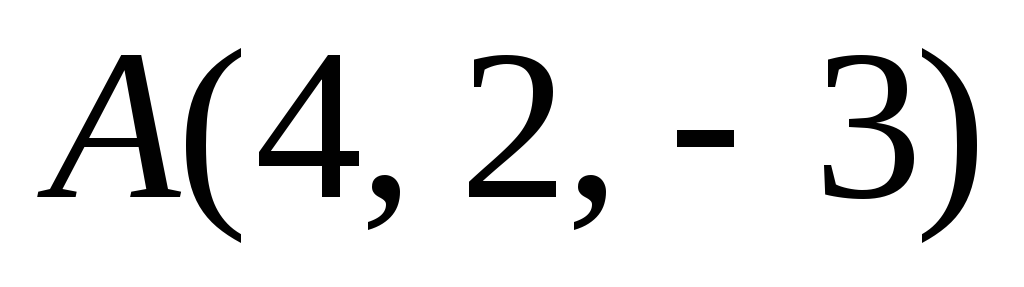. Найти величину и направляющие косинусы момента этой силы относительно точки.

4. Дано: . Найти площадь.

5. Дано: . Найти

площадь ,длину высоты.

Дома.

1. Дано: . Вычислить.

2. Силы приложены к точке. Найти величину и направляющие косинусы момента равнодействующей этих сил относительно точки.

3. Даны последовательно координаты вершин параллелограмма:. Найти

площадь параллелограмма ,длину высоты.

Ответы:

Смешанное произведение.

1. Вектор перпендикулярен векторами, тройка– правая,.

Найти .

2. При каком значении компланарны векторы?

3. Лежат ли точки в одной плоскости?

4. Даны координаты вершин тетраэдра: . Найти его объем.

5. Даны координаты вершин тетраэдра: . Найти длину высоты.

Дома. 1. Компланарны ли векторы?

2. Дано: .

Найти: в) объем тетраэдра ; г)длину высоты тетраэдра.

Ответы:

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Прямая на плоскости.

1. Построить прямые:

2. Дано: . Какие из точек принадлежат прямой?

3. Найти точки пересечения прямых

4. Дана прямая . Составить уравнение прямой, проходящей через точку

а) параллельно ; б) перпендикулярно.

5. Дано: . При каких значенияхпрямыеиа) параллельны; б) перпендикулярны?

6. Составить уравнение серединного перпендикуляра к , если.

7. Найти точку , симметричную точкеотносительно прямой.

8. Дано: . Найти центр описанной околоокружности.

9. Найти центр масс , где.

10. В ромбе даны. Составить уравнения диагоналей ромба.

11. Найти площадь , где.

12. Даны три последовательные вершины параллелограмма . Найти, составить уравнения сторон и диагоналей.

Дома.Дан:. Найти а) центр описанной окружности; б) центр масс; в) площадь.

Ответы: