Построение доверительного интервала дисперсии

В курсе математической статистики доказано, что в выборке из нормальной ге-

неральной совокупности с параметрами случайная величина,

где – оценка неизвестной дисперсии, равная, имеет распределение

с n степенями свободы. Если параметр неизвестен, то в выраженииможно заменитьна его оценку; в этом случае случайная величинатакже имеет распределение, но уже с, а не сn степенями свободы.

Пусть числа выбраны таким образом, что

, (9)

где – заданная доверительная вероятность.

Равенство (9) означает, что c вероятностью . Последнее двойное неравенство эквивалентно следующему:

. (10)

Следовательно, 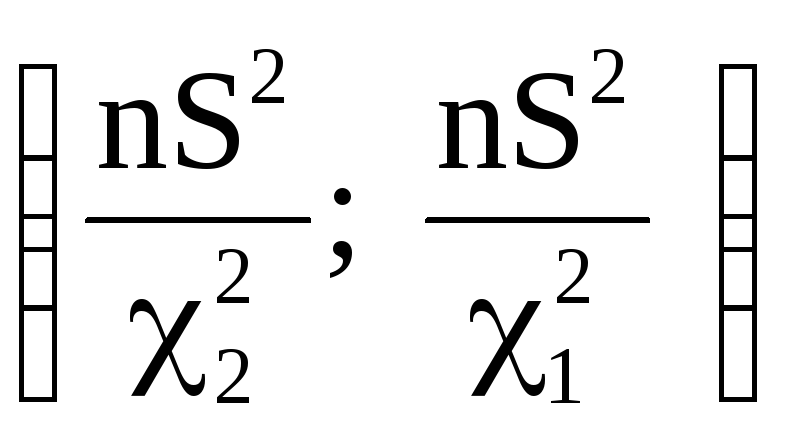является доверительным интервалом дисперсии, соответствующим доверительной вероятности.

Однако по заданной вероятности можно построить множество доверительных интервалов для дисперсии. Принятовыбирать так, чтобы вероятностибыли равны и равны(рис. 1).

Соответствующие значения могут быть определены по таблице А2.

Замечание. При больших объемах выборок можно воспользоваться тем, что рассмотренные оценки математического ожидания и дисперсии распределены

асимптотически нормально.

Рисунок 1. График плотности - распределения с

степенями свободы

x

Пример выполнения и оформления лабораторной работы

Дана выборка объемом (табл. 1) из нормальной генеральной совокупности.

Таблица 1

№ п/п	Элементы выборки	№ п/п	Элементы выборки	№ п/п	Элементы выборки	№ п/п	Элементы выборки
1	0,047	6	0,496	11	-1,7888	16	0,118
2	- 0,451	7	- 0,748	12	- 0,855	17	0,242
3	1,661	8	- 0,083	13	0,095	18	1,739
4	1,290	9	- 0,312	14	1,192	19	- 0,412
5	0,380	10	-1,372	15	- 0,059	20	- 0,426

Найдем по формулам (1) и (3) оценки математического ожидания и дисперсии, ;

; .

Так как объем выборки невелик, для построения доверительного интервала для математического ожидания воспользуемся формулой (8):

.

Доверительную вероятность положим равной 0,95, . По таблице А3 по заданным иопределим.

Доверительный интервал для математического ожидания, соответствующий доверительной вероятности :

или .

При построении доверительного интервала дисперсии положим . Тогда.определим из условия;определим из условия(рис. 1).

По таблице А2 по заданным вероятностям Р (0,01 и 0,99) и заданному числу степеней свободы находим.

Доверительный интервал дисперсии, соответствующий доверительной вероятности , определяется по формуле (10):

.