Лабораторная работа 3 Построение доверительных интервалов математического ожидания и дисперсии в случае выборки из нормальной генеральной совокупности

Порядок выполнения работы

1. По данной выборке найти оценки математического ожидания и дисперсии.

2. Найти доверительный интервал для математического ожидания, соответствующий доверительной вероятности .

3. Найти доверительный интервал для дисперсии, соответствующий доверительной вероятности .

4. Составить отчет, в котором привести исходный статистический материал, использованные расчетные формулы, результаты счета.

5. Ответить устно на контрольные вопросы.

Нахождение оценок математического ожидания и дисперсии

По данной выборке находим оценки математического ожидания и дисперсии генеральной совокупности:

, (1)

(2)

или , (3)

где n - объем выборки, – элементы выборки.

Построение доверительного интервала математического ожидания

Полученные на первом этапе оценки называютсяточечными и являются случайными величинами, изменяющимися от выборки к выборке. Использование точечных оценок, построенных по выборкам малого объема (n ~ 10), может привести к существенным ошибкам. Например, среднее арифметическое , как оценка математического ожидания, имеет дисперсию. При большихn дисперсия оценки мала, и реализация оценки весьма тесно концентрируется около своего математического ожидания, равного. При малых объемах выборки дисперсия оценкиможет быть большой.

В случае использования точечных оценок, построенных по выборкам малого объема, необходимо указать, с какой степенью уверенности можно говорить о том, что отклонение оценки а* от оцениваемого параметра а не превзойдет определенную величину.

По заданной вероятности (как правило, 0,9; 0,95; 0,99) определим число, такое, что, или, что то же самое,

(4)

Интервал , с вероятностьюсодержащий истинное значение оцениваемого параметра, называетсядоверительным интервалом; границы его - случайные величины. Вероятность называетсядоверительной вероятностью.

Доверительный интервал может быть несимметричным относительно оцениваемого параметра.

В случае выборки из нормальной генеральной совокупности оценка имеет

нормальное распределение с параметрами , где- параметры нормаль-

ной генеральной совокупности. Если параметр известен, то

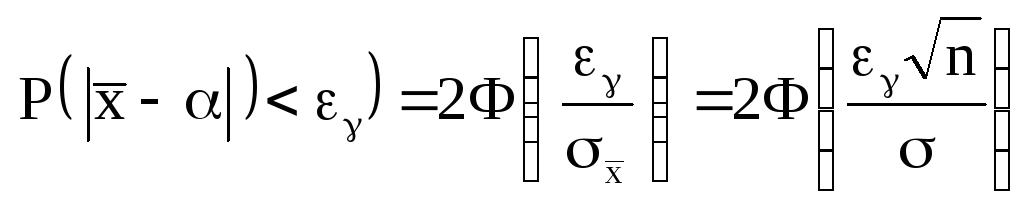, (5)

где 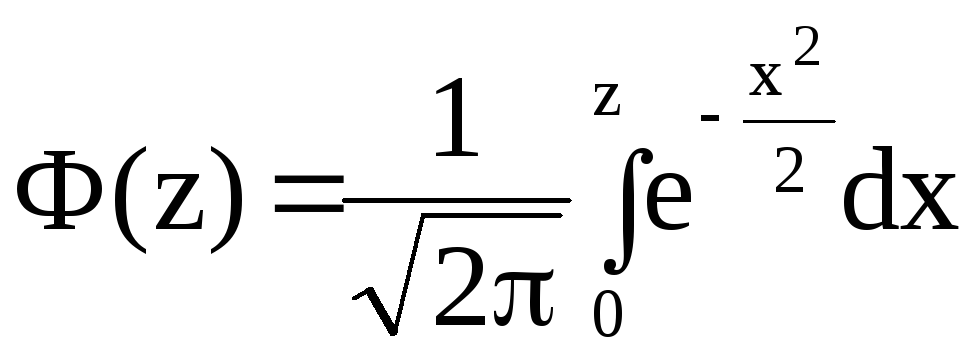- функция Лапласа. Из равенства

, (6)

используя таблицу А1, можно определить . Интервалявляется доверительным интервалом для математического ожидания, соответствующим доверительной вероятности.

Если параметр не известен, то простая замена этого параметра в формуле (5) его оценкойв случае малой выборки может привести к существенным ошибкам.

В этом случае можно воспользоваться случайной величиной , где- математическое ожидание генеральной совокупности,- оценки параметров нормальной генеральной совокупности. В курсе математической статистики доказывается, что случайная величина t в выборке из нормальной генеральной совокупности имеет распределение Стьюдента (t - распределение) с (n-1) степенями свободы, распределение, не зависящее от параметров генеральной совокупности.

Пусть число таково, что, (7)

где – заданная доверительная вероятность.

Равенство (7) означает, что с вероятностью. Последнее

неравенство эквивалентно следующему:

. (8)

Следовательно, интервал является доверительным интервалом математического ожидания, соответствующим доверительной вероятности.

Значения , зависящие оти числа степеней свободы, могут быть определены по таблице А3.