- •Тема 1. Изображение точек на комплексном чертеже.
- •Тема 2. Прямая. Взаимное расположение прямых.
- •Тема 3. Плоскость. Главные линии плоскости.
- •Тема 4. Взаимное расположение прямой и плоскости.
- •Тема 5. Взаимное положение плоскостей.
- •Тема 6. Поверхности. Принадлежность точек и линий поверхностям.
- •Тема 7. Пересечение поверхности с плоскостью
- •Тема 8. Пересечение прямой линии с поверхностью
- •Тема 9. Взаимное пересечение поверхностей. Метод секущих плоскостей
- •Тема 10. Взаимное пересечение поверхностей. Способ сферического посредника
- •Список литературы:
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Рабочая тетрадь для решения задач
по дисциплинам «Начертательная геометрия»,
«Инженерная графика» и «Инженерная и компьютерная графика»
(для студентов очной и заочной форм обучения)
Омск - 2013
Составители: Притыкин Ф.Н.
Рецензент: Косолапова Р.В. к.п.н., доцент кафедры «Начертательная геометрия, инженерная и машинная графика» СибАДИ
Рабочая тетрадь для решения задач по дисциплинам «Начертательная геометрия» , «Инженерная графика» и «Инженерная графика и компьютерная графика» для студентов очной и заочной форм обучения / Притыкин Ф.Н, Омск: Изд-во ОмГТУ, 2013. – 32 с.
Рабочая тетрадь составлена в соответствии с государственным образовательным стандартом высшего профессионального образования дисциплин «Начертательная геометрия», «Инженерная графика» и «Инженерная графика и компьютерная графика». Предназначен для студентов очной и заочной форм обучения.
Печатается по решению редакционно-издательского совета Омского государственного университета.
© Притыкин Ф.Н., 2013
© Омский государственный технический университет, 2013
ВВЕДЕНИЕ
Рабочая тетрадь предназначена для студентов первого курса очной и заочной форм обучения, изучающих дисциплины «Начертательная геометрия , «Инженерная графика» и «Инженерная и компьютерная графика». Самостоятельная практическая работа студентов по указанным дисциплинам включает решение задач в рабочей тетради и выполнение графических работ на чертежной бумаге (ватмане). Графические работы следует выполнять в соответствии со стандартами, устанавливающими правила оформления чертежей.
В рабочей тетради приведены условия задач, показаны примеры их выполнения по основным разделам дисциплин. Перед решением задач рекомендуется изучить теоретический материал, отраженный в перечне вопросов, приведённых в начале каждого раздела. Если указанные вопросы вызывают затруднения, то необходимо обратится к учебному пособию с целью изучения соответствующих разделов дисциплин.
Графические построения при решении задач в рабочей тетради выполняются карандашом с использованием чертежных инструментов. Точки и линии должны быть обозначены буквами или цифрами (размер шрифта № 5).
Принятые обозначения
1. Точки в пространстве обозначаются прописными буквами латинского алфавита – А, В, С,… или цифрами 1, 2, 3,…
2. Линии – строчными буквами латинского алфавита – а, b, c,…
3. Плоскости – строчными буквами греческого алфавита – α, β, γ, δ, ε … ; плоскости проекций – П1, П2, П3, …
4. Проекции точек, линий и плоскостей обозначают теми же буквами, только с индексами: например, проекции на плоскости П1 – А1, В1, a1, b1, α1, на плоскости П2 – А2, В2, a2, b2, α2. Используются следующие обозначения:
= – совпадение, равенство, результат действия;
 –скрещивание
прямых;
–скрещивание
прямых;
|| – параллельность;
![]() –перпендикулярность;
–перпендикулярность;
– принадлежность элемента множеству;
– принадлежность подмножества множеству;
![]() –пересечение,
например
–пересечение,
например ![]() а=А
– пересечение плоскости
с прямой а определяет точку А.
а=А
– пересечение плоскости
с прямой а определяет точку А.
Тема 1. Изображение точек на комплексном чертеже.
Вопросы:
Что представляет собой метод ортогональных проекций?
Что называют координатами точки?
Что такое комплексный чертеж точки?
Назовите законы проекционной связи.
Какие точки называются конкурирующими?
Задачи:
Построить проекции точек А(40,20,30), В(40,30,0), С(0,0,30) и D(0,10,20) на комплексном чертеже.
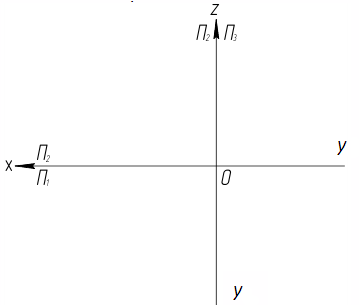
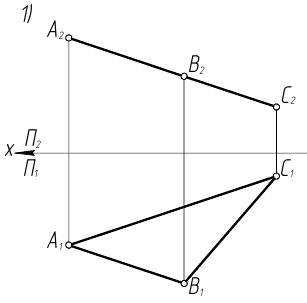
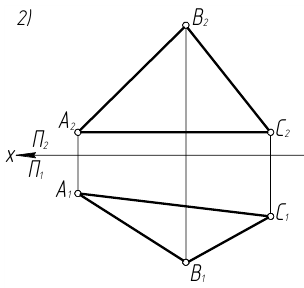
Точки А, В и С принадлежат плоскостям проекций. Построить недостающие проекции этих точек и указать в какой плоскости каждая из них располагается.
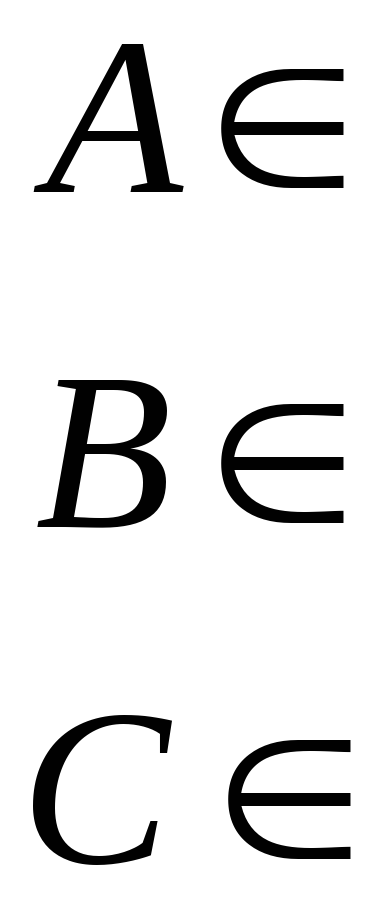
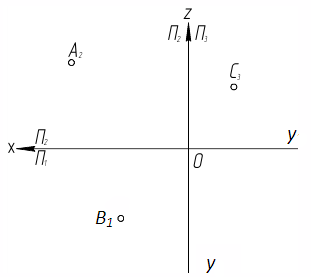
Тема 2. Прямая. Взаимное расположение прямых.
Вопросы:
Какую прямую называют прямой общего положения, прямой уровня и проецирующей прямой?
Как расположены проекции прямой, принадлежащей одной из плоскостей проекций?
Сформулируйте условие принадлежности точки прямой.
Сформулируйте признаки, по которым можно судить о взаимном положении двух прямых, изображенных на комплексном чертеже.
Когда прямой угол проецируется в прямой угол на одну из плоскостей проекций?
Как преобразовать на комплексном чертеже прямую общего положения: а) в прямую уровня
б) в проецирующую прямую?
Задачи:
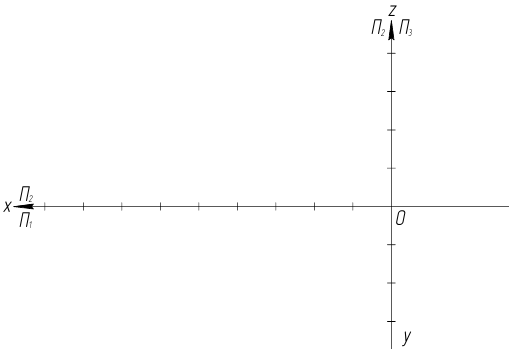
Заданы точки А(90,30,40), В(10,20,15), С(60,20,40) и D(30,40,15). Построить проекции отрезков АВ и СD, обозначить и записать координаты фронтально и горизонтально конкурирующих точек. Проекции отрезков прямых выполнить только на П1 и П2.
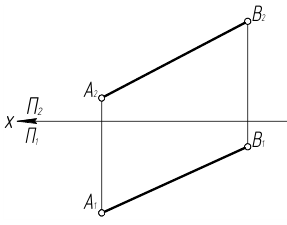
Отложить на отрезке АВ отрезок АК=20мм и определить угол наклона отрезка АВ к плоскости проекций П1.
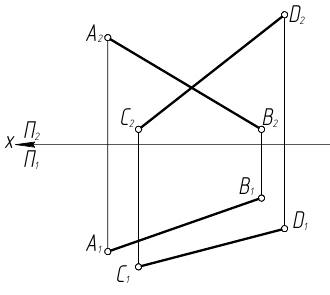
Пересечь прямые АВ и СD прямой MN, отстоящей от плоскости П1 на расстоянии 15 мм.
Даны две скрещивающиеся прямые с и d. Построить отрезок МN, являющийся кратчайшим расстоянием между этими прямыми.
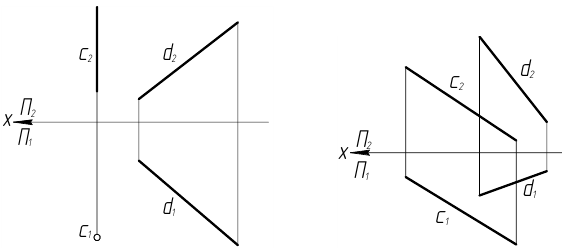
Заданы точка А(А1,А2) и прямая ВС общего положения. Построить сферу с центром в точке А, касательную к прямой ВС.
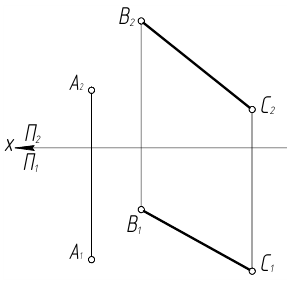
Пример 1. Даны две параллельные прямые АВ и CD. Определить кратчайшее расстояние между ними (рис. 1).
Решение этой задачи выполняем в следующей последовательности:
а)
Определяем натуральные величины отрезков
заданных прямых, для этого вводим П4
//
АВ // СD
и П4
![]() П1.
На комплексном чертеже Х1
//
A1B1
//
C1D1;
П1.
На комплексном чертеже Х1
//
A1B1
//
C1D1;
б)
Заданные прямые преобразуем в проецирующее
положение
(П5
![]() AВ,
П5
AВ,
П5
![]() CD
и П5
CD
и П5
![]() П4).
На комплексном чертеже Х2
П4).
На комплексном чертеже Х2
![]() А4В4
и
Х2
А4В4
и
Х2
![]() C4D4.
Длина M5N5
является искомым расстоянием.
C4D4.
Длина M5N5
является искомым расстоянием.
д)
Используя проекционную связь находим
положения проекций отрезка MN
на П1
и П2.
M4N4
![]() A4B4
, точка M4
на A4B4
взята произвольно.
A4B4
, точка M4
на A4B4
взята произвольно.
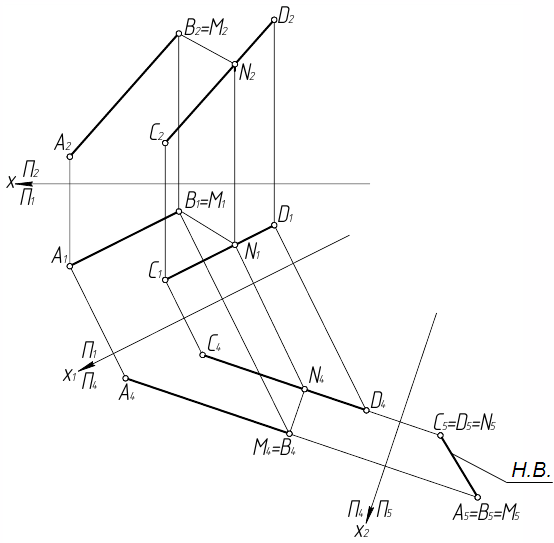
Рис. 1
Тема 3. Плоскость. Главные линии плоскости.
Вопросы:
Какими способами можно задать плоскость на комплексном чертеже?
Какие плоскости называются плоскостями общего положения, проецирующими или плоскостями уровня?
Сформулируйте условия принадлежности точки и прямой плоскости?
Какие линии называются главными линиями плоскости?
Как на комплексном чертеже преобразовать плоскость общего положения в плоскость проецирующую и в плоскость уровня?
Задачи:
Заданы плоскость Σ (ΔABC), и точки D и E в этой плоскости. Через точку Е провести горизонталь h, через точку D – фронталь f принадлежащие заданной плоскости.
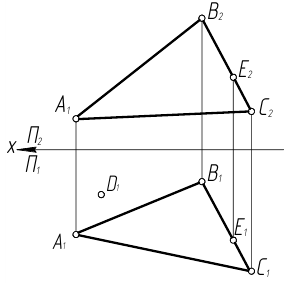
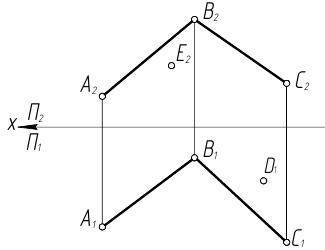
Построить недостающие проекции точек E и D, принадлежащих плоскости Σ (АВ ∩ ВС).
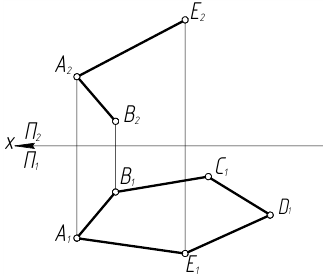
10. Задан плоский пятиугольник ABCDЕ горизонтальными и фронтальными проекциями двух смежных сторон. Достроить его фронтальную проекцию.
Задан треугольник АВС. Найти центр окружности, описанной вокруг заданного треугольника.