МЕТОДИЧКИ / Методички (мол) / №28 -

10

Лабораторная работа №28

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТИ ГАЗА МЕТОДОМ КЛЕМАНА И ДЕЗОРМА

Принадлежности: экспериментальная установка в сборе.

Цель работы:

1) Изучить процессы, происходящие с идеальным газом.

2) Определить коэффициент Пуассона.

Введение. Термодинамической системой называется система, состоящая из большого числа частиц – атомов и молекул, которые совершают тепловое движение и, взаимодействуя между собой, обмениваются энергиями. Простейшей термодинамической системой является газ.

Любое состояние газа может быть описано тремя основными параметрами: объемом V, давлением P и температурой Т.

Уравнение, которое связывает эти параметры, называется уравнением состояния. Таким уравнением для идеального газа является уравнение Менделеева – Клайперона:

(1)

Согласно первому закону термодинамики, теплота, подводимая к термодинамической системе, расходуется на увеличение ее внутренней энергии U и на работу, совершаемую системой против внешних сил

(2)

Теплоемкость газа зависит от условий ее нагревания. Она разная в различных процессах.

Удельная теплоемкость газа (с_уд) – скалярная физическая величина, равная количеству теплоты, которое необходимо подвести к единице массы вещества, чтобы повысить его температуру на один градус:

(3)

Молярная теплоемкость (С) – скалярная физическая величина, равная количеству теплоты, которое необходимо подвести к одному молю вещества, чтобы повысить его температуру на один градус. Она связана с удельной теплоемкостью соотношением:

(4)

Учитывая, что изменение внутренней энергии идеального газа

(5)

А элементарная работа, совершаемая газом,

(6)

Подставив выражение для из (2) в (4), получаем формулу молярной теплоемкости:

(7)

Пользуясь этой формулой, можно определить теплоемкость газа в любом процессе.

Изохорический процесс. Изохорическим называется процесс, при котором объем газа остается постоянным(∆V=0). При этом процессе работа не совершается (), и вся теплота подводимая к газу, идет на увеличение его внутренней энергии.

Первый закон термодинамики принимает вид: ∆Q=∆U.

Молярная теплоемкость газа в этом процессе равна

Подставив вместо ∆U выражение (5), получаем:

Здесь – число степеней свободы молекулы,

– универсальная газовая постоянная.

Изобарический процесс. Процесс называется изобарическим, если давление газа остается постоянным (P=const).

В этом процессе и объем газа, и его температура изменяются.

Следовательно, теплота, подведенная к газу, расходуется и на работу и на увеличение внутренней энергии газа.

Молярная теплоемкость газа в этом случае определяется соотношением:

Подставив вместо ∆U выражение (5), а вместо выражение

,

Получим для 1 моля газа:

или (9)

Соотношение (9) называется уравнением Майера. Теплоемкость газа при постоянном давлении больше, чем теплоемкость газа при постоянном объеме, так как в этом процессе подведенная теплота идет не только на увеличение внутренней энергии газа, но и на работу, совершаемую газом против внешних сил. Из уравнения Майера вытекает физический смысл универсальной газовой постоянной R.Эта физическая величина численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.

Изотермический процесс. Процесс, протекающий при постоянной температуре (T=const),

Называется изотермическим. В этом процессе . Следовательно, внутрянняя энергия газа не изменяется (). Вся теплота, подводимая к газ, расходуется на совершение работы: ∆Q=∆А. Теплоемкость в этом процессе равна

Таким образом, при этом процессе газ ведет себя как тело, обладающее бесконечно большой теплоемкостью.

Адиабатический процесс. Процесс, протекающий без теплообмена с окружающей средой, называется адиабатическим. В этом случае

∆Q=0, 0,

Газ совершает работу за счет уменьшения своей внутренней энергии. При адиабатном расширении газ охлаждается, а при адиабатном сжатии нагревается.

Теплоемкость газа в адиабатическом процессе равна

=0

Большое практическое значение имеет отношение теплоемкостей газа , где носит название коэффициента Пуассона и входит в уравнение Пуассона, описывающее адиабатический процесс . Коэффициент зависит от числа степеней свободы молекулы и для различных газов оказывается различным. Его определяют опытным путем.

Описание установки и методики измерений. В стеклянный баллон 1 рис 1, соединенный с компрессором 2, через напускной кран 3 накачивается воздух. Клапан сброса воздуха 4, находящийся на верхней крышке установки позволяет резко уменьшить давление в баллоне практически без теплообмена с окружающей средой. На рис 2 представлена передняя панель установки, на которой размещаются тумблер Сеть» 7, тумблер «Компрессор» 8, водяной U – манометр 5, кран 3 перепуска воздуха со следующими положениями. ОТКРЫТ – положение ручки крана на данной отметке открывает линию к компрессору 2.ЗАКРЫТ – положение ручки крана на данной отметке перекрывает баллон 1.РЕГУЛИРОВАНИЕ УРОВНЯ – положение ручки крана на данной отметке позволяет отрегулировать уровень воды в коленах U- манометра после заполнения баллона воздухом.

Установка работает следующим образом. В баллон компрессором 2 накачивается воздух. Давление в баллоне повышается и становится равным

3

Р₁ = Р₀ + h₁, (1)

Где Р₀ – атмосферное давление, h₁ - избыток давления воздуха в баллоне над атмосферным. Величина h₁ определяется по водяному манометру 5. Первое состояние газа характеризуется параметрами Р₁, V₁, Т₁ (Т₁ - комнатная температура). На рис.3 это состояние представлено точкой 1. После выравнивания температур воздуха в баллоне и окружающей среды, осуществляется быстрый сброс давления через выпускное отверстие с клапаном 4. Воздух в баллоне расширяется от объема V₁ до некоторого объема V₂ , выходя частично в атмосферу. Давление в баллоне упадет до атмосферного Р₀. Газ расширяется очень быстро, поэтому теплообмен с окружающей средой не успевает осуществиться. Происходит адиабатический процесс, газ охлаждается до некоторой температуры Т_2, которая ниже комнатной. Это состояние газа характеризуется параметрами Р₀, V₂, Т₂ и на рис.3 представлено точкой 2. После того, как клапан сброса закрылся, осуществляется изохорный процесс теплообмена с окружающей средой. Температура воздуха в баллоне приближается к температуре окружающей среды (комнатной) Т₁ и давление газа станет равным Р₂ .Это третье состояние газа характеризуется параметрами Р₂, V₂, Т₁ и на рис.3 представлено точкой 3.Давление газа в этом состоянии равно

Р₂ = Р₀ + h₂, (2)

Где h₂ - показание манометра после того, как температура газа стала равна комнатной.

Так как переход от состояния 2 к состоянию 3 произошел без изменения объема, то используя закон Шарля можно записать

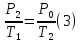
К процессу адиабатического расширения, т.е. к переходу из состояния 1 в состояние 2 , может быть применен закон Пуассона, который удобно записать в следующей форме

Где γ – отношение удельных теплоемкостей газа при постоянном давлении и при постоянном объеме С_р/Сv.Подставляя значение Р₁ из формулы (1) в формулу (4) получим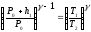

Преобразуем

(5)

Каждую скобку равенства (5) представим в виде биномиального ряда.

- биномиальный ряд

В силу малости дробных слагаемых в скобках по сравнению с единицей ограничимся двумя первыми членами разложения.

Откуда

На основании выражений (2) и(3) получим

Следовательно, можно записать

Откуда получаем формулу для определения показателя адиабаты.

Измерения

1. Включить установку тумблером «СЕТЬ». Повернуть ручку крана 3 в положение «ОТКРЫТ» 9 рис.2.Включить тумблер «КОМПРЕССОР». Накачивать воздух в баллон до красной линии на установке, при этом разность уровней жидкости в манометре должна быть не менее 20-25 см. После этого закрыть напускной клапан поворотом ручки крана 3 в положение «ЗАКРЫТ» и отключить компрессор.

2. Подождать 2-4 минуты, пока температура воздуха в баллоне не станет равна температуре окружающей среды.

3. Измерить разность уровней жидкости h₁в манометре рис.1. Полученное значение h₁ записать в таблицу.

4. Резко (но не сильно!) нажать и отпустить выпускной клапан 4. При этом газ адиабатически расширяется. Давление его становится равным атмосферному, а температура понижается.

5. Через 2-3 минуты уровни воды в манометре стабилизируются. Воздух в баллоне нагревается до комнатной температуры и его давление возрастает. Как только температура газа станет равной комнатной, давление примет определенное значение. После этого определить разность уровней h₂ в правом и левом колене манометра. Значение h₂ записать в таблицу.

6. Повторить пункты 1-6 не менее 7-10 раз. Следить за тем, чтобы начальная разность уровней в манометре была постоянной.

Обработка результатов измерений

1. По формуле (12) вычислите величину g для каждого измерения. Найдите ее среднее значение.

2. Вычислите полуширину доверительного интервала по формуле Стьюдента как для прямых измерений при доверительной вероятности р=0,95

.

3. Окончательный результат представьте в стандартном виде

, р=0,95.

4 .Определите относительную погрешность Dg /ágñ измерения γ.

5. Сравните полученное значение с тем, что дает молекулярно-кинетическая теория и которое можно вычислить по формуле

,

где i – число степеней свободы молекулы рассматриваемого газа.

Будем считать воздух однородным двухатомным газом (содержанием других газов, в том числе и водяного пара, пренебрежем, считая его незначительным). Что показывает сравнение?

6. Рассчитайте массу воздуха М₁ в баллоне в исходном состоянии 1 по формуле

.

7. Рассчитайте температуру газа Т₂ в баллоне к концу расширения (процесс1–2) по формуле

,где

Таблица

Давл. атмосфер. Р0 = Темпер. комн. Т1˚= Объем сосуда V=7л
№ изм.	h1	h2	h1 - h2	
Ср.

Контрольные вопросы

1. Запишите первое начало термодинамики. Что называется внутренней энергией.

2. Что называется теплоемкостью – удельной, молярной? Как теплоемкость различается в зависимости от процесса?

3. Почему С_р больше, чем С_V и на сколько? Каков физический смысл универсальной газовой постоянной R ?

4. Какой процесс называется адиабатическим? Напишите уравнение адиабаты и сравните его с уравнением изотермы.

5. Чему равно теоретическое и табличное значение g для воздуха? Почему полученное вами значение отличается от табличного?

6 .Почему на рис.2 кривая 3-4 идет круче кривой 1-2? Почему обе кривые идут круче кривой 1-3?

7. Вывод рабочей формулы (7).

Список рекомендуемой литературы

1.Сивухин Д.В. Общий курс физики.Т 2. Термодинамика и молекулярная физика. М.: Физматлит, 2006. §21-22.

2.Савельев И.В. Курс общей физики. Т.1. Механика и молекулярная физика. СПб.: Лань, 2005.§87-88.

3.Трофимова Т.И. Курс физики. М.: Высшая школа, 1990. С.91-96.

4.Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 1989. §9.6; 10.12.