Работа № 107

Изучение движения гироскопа

Принадлежности: прибор FPM , штангенциркуль.

Цель работы: изучение прецессионного движения гироскопа.

Введение.

Гироскоп – быстровращающееся симметричное твердое тело, ось вращения (ось симметрии) которого может изменять свое направление в пространстве. Свойствами гироскопа обладают вращающиеся небесные тела, артиллерийские снаряды, роторы турбин, устанавливаемых на судах, винты самолетов и т. д. В современной технике гироскоп – основной элемент всевозможных гироскопических устройств или приборов, широко применяемых для автоматического управления движением самолетов, судов, торпед, ракет и в ряде других систем гироскопической стабилизации, для целей навигации (указатели курса, поворота, горизонта, стран света), для измерения угловых или поступательных скоростей движущихся объектов (ракет) и во многих других случаях.

Ч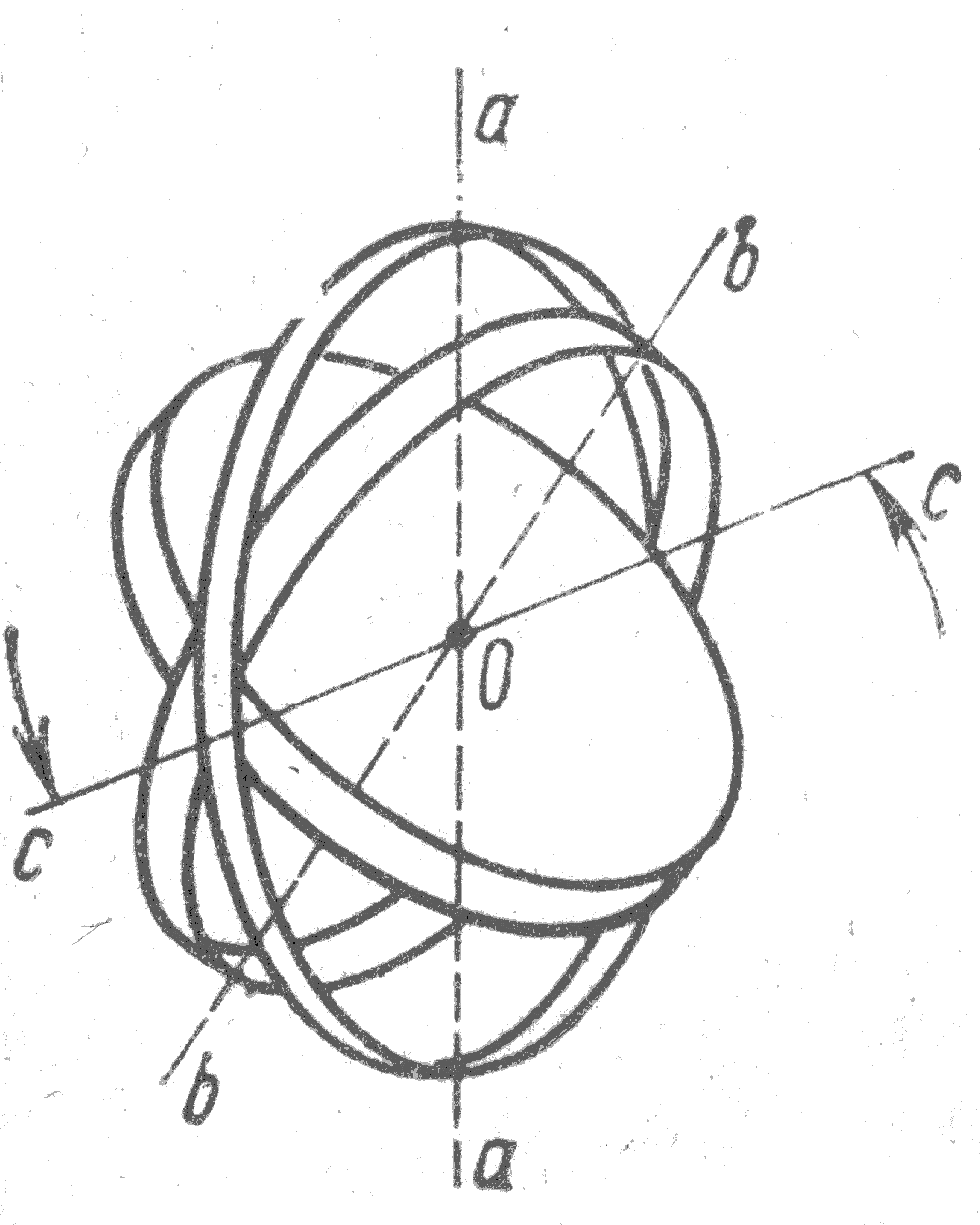тобы ось гироскопа могла поворачиваться в любом направлении, его помещают в карданов подвес (рис.1). Все три оси подвеса пересекаются в одной точке О – центре карданова подвеса. Закрепленный в таком подвесе гироскоп имеет три степени свободы и может совершать любой поворот около центра подвеса. Если центр тяжести совпадает с центром подвеса, гироскоп называют уравновешенным.

Теория гироскопа относится к разделу динамики твердого тела. В общем виде движение гироскопа представляет собой одну из самых трудных задач механики. Однако в тех случаях, когда гироскоп быстро вращается относительно главной оси инерции и медленно относительно других осей, возможен элементарный анализ его движения. Движение твердого тела, имеющего одну закрепленную точку, описывается уравнением:

Рис.1.

Для анализа движения гироскопа уравнение (1) удобно записать в такой форме

Откуда следует, что изменение момента количества движения за время равно произведению суммарного момента всех внешних сил на время его действия и совпадает с ним по направлению.

В гироскопе различают три направления (оси), проходящие через неподвижную точку тела:

1) направление мгновенной оси вращения, определяемое направлением вектора мгновенной угловой скорости,

2) направление главного момента количества движения (момента импульса),

3) ось симметрии тела.

Все три оси в общем случае могут не совпадать по направлению, что значительно усложняет анализ движения гироскопа. Только при очень быстром вращении его вокруг оси симметрии вектор главного момента количества движения и вектор мгновенной угловой скорости практически совпадают с направлением оси симметрии. Поэтому о движении мгновенной оси вращения можно судить по движению оси симметрии гироскопа.

При отсутствии момента внешних сил () из уравнения (1) следует , т.е. главный момент количества движения (ось симметрии гироскопа) остается в пространстве неподвижным. При кратковременном воздействии внешних сил (при ударе) очень мало, поэтому на основании уравнения (2) будут очень малы и изменения ориентации , и оси симметрии гироскопа. При длительном воздействии внешних сил направление в пространстве вектора главного момента количества движения, мгновенной угловой скорости и оси симметрии гироскопа будут изменяться. В том случае, когда направление внешних сил все время одно и то же, ось гироскопа описывает круговую коническую поверхность (рис. 2). Такое движение гироскопа называют ПРЕЦЕССИЕЙ.

ω

Ω

Рис.2.

Цель работы: изучение прецессионного движения гироскопа.

Пусть гироскоп быстро вращается вокруг оси ОУ с угловой скоростью ω (рис.3). Если J - его момент инерции относительно оси ОУ, то момент импульса (момент количества движения) гироскопа

есть вектор, направленный по оси ОУ. Если к концу оси гироскопа подвесить груз на расстоянии α от центра О, то на гироскоп будет действовать момент силы тяжести, направленный горизонтально перпендикулярно плоскости, в которой лежат ось гироскопа и сила тяжести mg

.

Под действием момента силы тяжести ось гироскопа будет прецессировать вокруг вертикальной оси ОZ и в горизонтальной плоскости. За малый промежуток времени вектор момента импульса гироскопа вместе с осью гироскопа повернется на малый угол . Изменение вектора момента импульса (разность векторов ₁ и ₂ момента импульса в конечном и начальном положениях) лежит в горизонтальной плоскости и направлено в сторону прецессии (рис.3)

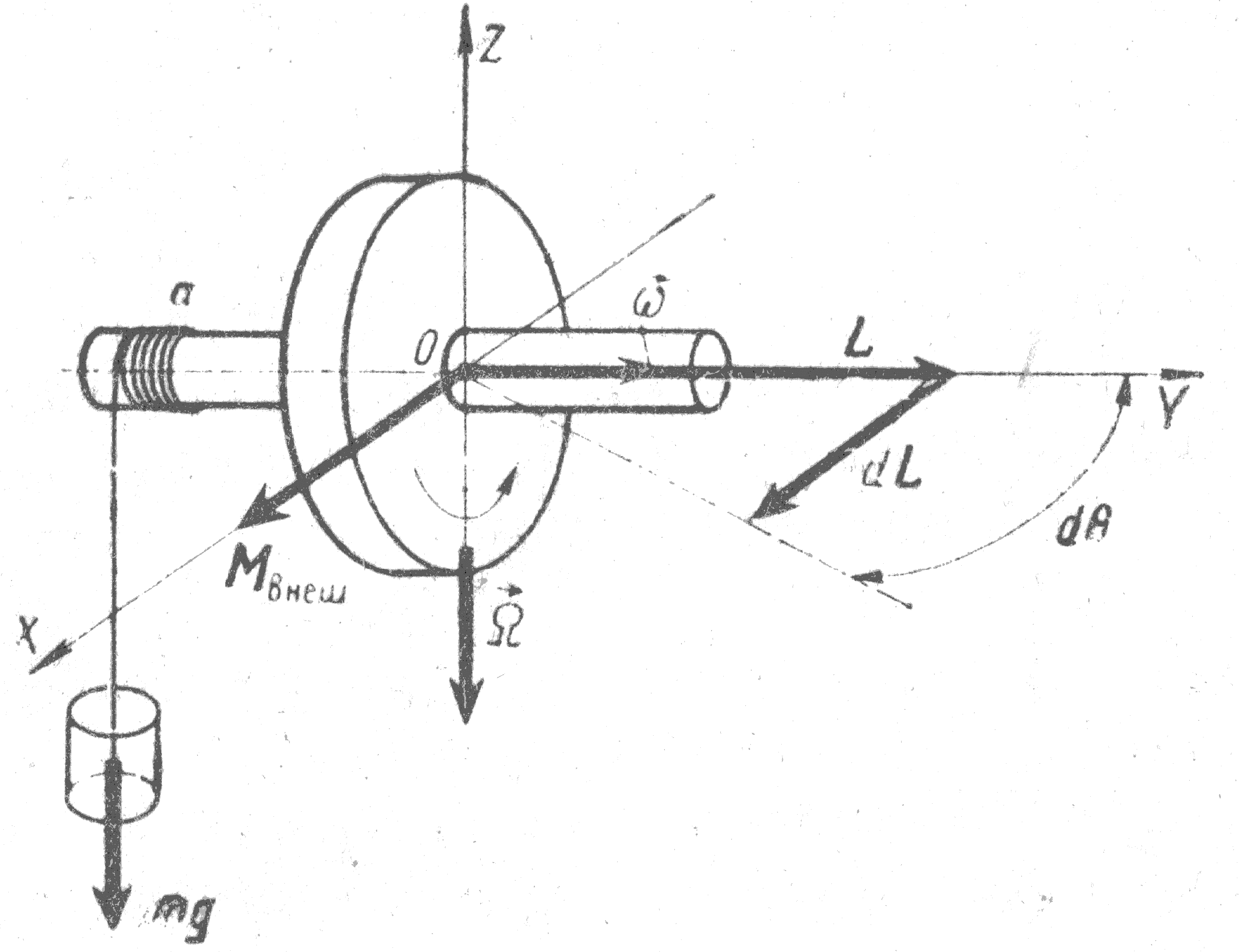
Рис.3.

Если момент внешних сил достаточно мал, то можно считать, что вектор постоянен по модулю, он изменяется лишь по направлению, поэтому

Разделим обе части последнего равенства на :

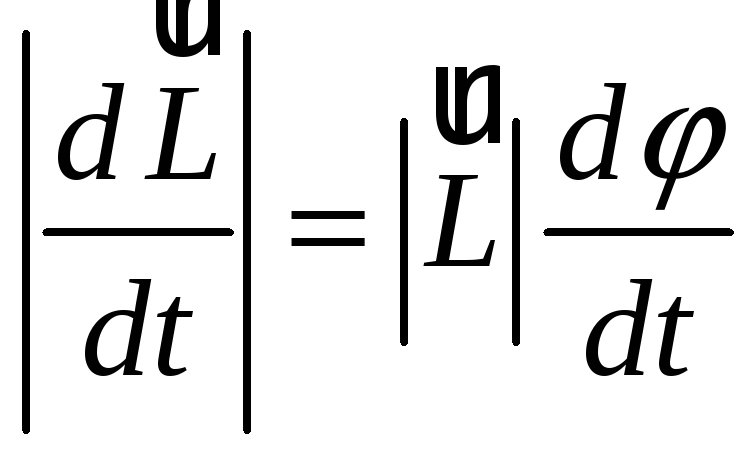
откуда

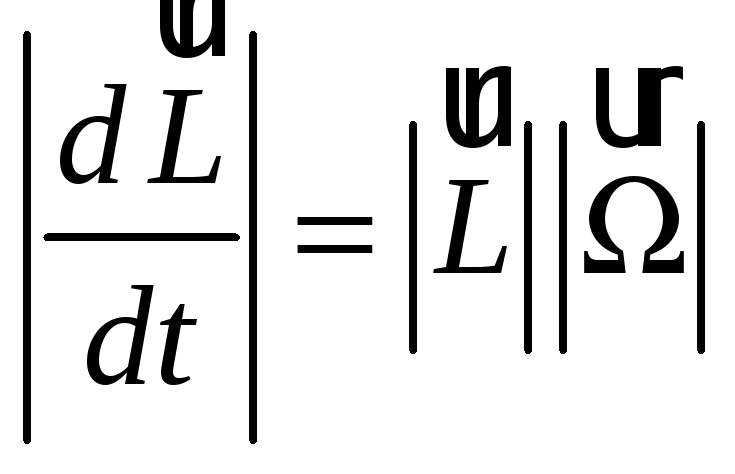
где угловая скорость вращения гироскопа вокруг вертикальной оси ОZ (угловая скорость прецессии).

Уточним, что значит достаточно малый момент внешних сил.

Если угловая скорость , то определяется в основном значением , т.е.

,

а это значит, что .

Таким образом, должен быть таким, чтобы гироскоп вращался вокруг оси ОZ гораздо медленнее, чем вокруг оси ОУ.

Из уравнения моментов следует, что

.

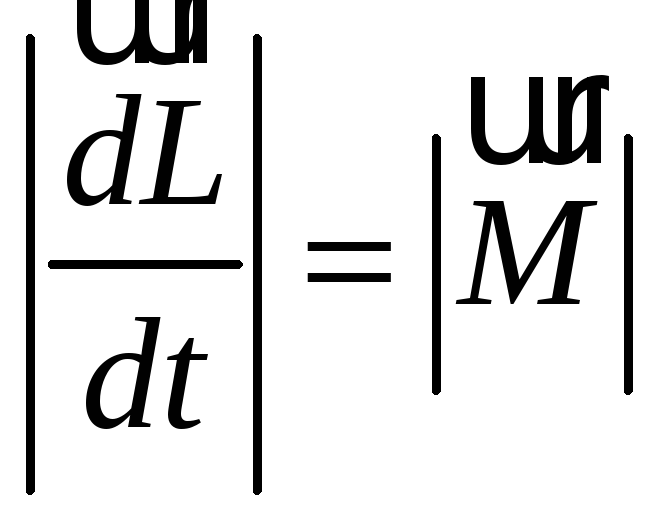Подставляя это выражение в (7) , получаем связь между угловой скоростью прецессии и приложенным моментом

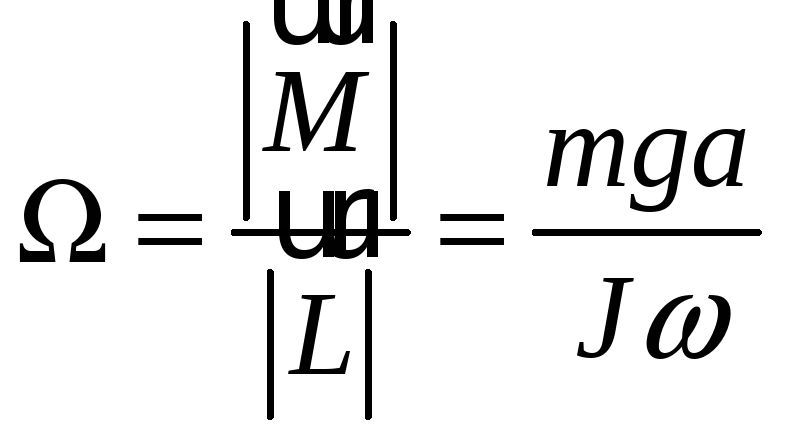(8)

Где - масса груза, - плечо силы тяжести груза, - момент инерции гироскопа относительно горизонтальной оси, - угловая скорость вращения гироскопа.