12. Работа, совершаемая постоянной и переменной силой. Мощность.

Работа силы Fна перемещениеΔrназывается скалярная величинаdA=F*dr=F*cosα*ds=Fsds, где α – угол м/у векторамиFиdr,ds=(dr) – элементарный путь,Fs– проекция вектораFна dr

Единица работы – джоуль. 1 Дж – работа соверш силой в 1 Н на путь в 1 м.

Мощность характеризует быстроту совершения работы и равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.

N=F*Vединица мощности – ватт.

1 ВТ – мощность, при которой за время 1 сек совершается работа 1 Дж

13. Кинетическая энергия и связь энергии и работы.

Физическая величина, равная половине произведения массы тела на квадрат его скорости – кинетическая энергия. – это энергия, которой обладает тело вследствие своего движения.

Изменение работы A=

Работа равнодействующих сил, приложенный к телу, равна изменению кинетической энергии тела. Выражается в Дж.

Если начальная скорость движения тела массой mравна 0 и тело увелич свою скорость доV, то работа силы равна конечному значению кинетической энергии тела.

A=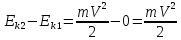

Кинетическая энергия тела массой m, движущегося со скоростью V, равна работе, которую даолжна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

14. Потенциальные и непотенциальные поля. Консервативные и диссипативные силы. Потенциальная энергия.

Силу , действующую на материальную точку, называют консервативной или потенциальной, если работа , совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло:

Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака консервативной силы, так как величина меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории , например , работа консервативной силы равна нулю.

Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.

Потенциальные силы создают стационарное поле, в котором работа силы зависит только от начального и конечного положений перемещаемой точки

Работа потенциальной силы при перемещении точки по замкнутой траектории L равна нулю

Если внешние тела, создающие рассматриваемое поле, могут двигаться относительно инерциальной системы, то это поле не будет стационарным. Но нестационарное полепотенциально, если работа, совершаемая силой F при мгновенном переносе точки ее приложения вдоль любой траектории L, равна нулю

К непотенциальнымотносятся диссипативные и гироскопические силы.Диссипативными силами называются силы, суммарная работа которых при любых перемещениях замкнутой системы всегда отрицательна (например, силы трения).Гироскопическими силаминазываются силы, зависящие от скорости материальной точки, на которую они действуют, и направленные перпендикулярно к этой скорости (например, сила Лоренца, действующая со стороны магнитного поля на движущуюся в нем заряженную частицу). Работа гироскопических сил всегда равна нулю.

Потенциальная энергия - это энергия, обусловленная взаимным расположением тел и характером их взаимодействия. При соответствующих условиях возможно изменение потенциальной энергии, за счет чего совершается работа. Для поднятия тела массой m на высоту необходимо совершить работу против сил тяготения Р:

,

знак минус перед интегралом, т.к. сила Р направлена в сторону противоположную изменению h.

Проинтегрируем это выражение:

Эта энергия пойдет на увеличение энергии замкнутой системы тело-Земля т.е. численно равна

Считая поверхности Земли , получим

Эта энергия системы тело - Земля и является потенциальной энергией тела, поднятого на высоту h: