42. Двигатель Карно. Кпд двигателя Карно. Теорема Карно.

Цикл Карно состоит из четырёх стадий:

1. Изотермическое расширение(на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуруT_H, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт емуколичество теплотыQ_H. При этом объём рабочего тела увеличивается.

2. Адиабатическое (изоэнтропическое) расширение(на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

3. Изотермическое сжатие(на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуруT_X, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплотыQ_X.

4. Адиабатическое (изоэнтропическое) сжатие(на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия:

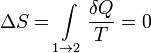
Поэтому цикл Карно удобно представить в координатах T и S температураэнтропияКПД тепловой машины Карно

Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

Отсюда коэффициент полезного действиятепловой машины Карно равен

Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины, будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Например, КПД идеального цикла Стирлингаравен КПД цикла Карно.

Первая теорема (более известна как формула Карно)

Первая теорема Карно: DG+DH+DF= |DG| + |DH| − |DF| =R+r

Пусть дан произвольный треугольникABC. Тогда суммаалгебраических расстояний(англ.) от центра описаннойокружностиDдо сторон треугольникаABCбудет равнаDF+DG+DH=R+r, гдеr— радиус вписанной окружности, аR— описанной. Знак расстояния принимается отрицательным тогда и только тогда, когдаотрезокDX(X = F, G, H) целиком лежит вне треугольника. В ее доказательстве используется теорема Птолемея

Первая теорема Карно:DG+DH+DF= |DG| + |DH| − |DF| =R+r

Вторая теорема (известная также как критерий Карно)

Пусть дан треугольникАВСи точкиА₁, В₁, С₁на плоскости. Тогдаперпендикуляры, опущенные изА₁, В₁, С₁наВС, АС, ВСсоответственно, пересекаются в одной точке тогда и только тогда, когдаA₁B²−A₁C²+B₁C²−B₁A²+C₁A²−C₁B²= 0.

СледствиеПерпендикуляры, опущенные изА₁, В₁, С₁наAB, АС, ВСсоответственно, пересекаются в одной точке тогда и только тогда, когда перпендикуляры, опущенные изА, В, СнаВ₁С₁, А₁С₁, В₁С₁соответственно, пересекаются в одной точке.