
Высшая математика. Экзамен. 1-2 семестр / 2 сем / линейные пространства
.pdfГЛАВА 8. ЛИНЕЙНЫЕ ПРОСТРАНСТВА § 1. Определение линейного пространства
Обобщая известное из школьной геометрии понятие вектора, мы определим алгебраические структуры (линейные пространства), в которых можно построить n-мерную геометрию, частным случаем которой будет аналитическая геометрия.
Определение 1. Задано некоторое множество L={a,b,c,…} и поле P={ , , ,…}. Пусть в L определена алгебраическая операция сложения и определено умножение элементов из L на элементы поля P:
P, a L αa L .
Множество L называется линейным пространством над полем P, если выполняются следующие требования (аксиомы линейного пространства):
1.L коммутативная группа по сложению;
2.α(βa)=(αβ)a α,β P, a L;
3.α(a+b)=αa+αb α P, a,b L;
4.(α+β)a=αa+βa α,β P, a L;
5.a L справедливо следующее равенство: 1 a=a (где 1— единица поля Р).
Элементы линейного пространства L называются векторами (еще раз отметим, что их будем обозначать латинскими буквами a, b, c,…), а элементы поля P — числами (их обозначаем греческими буквами α, ,
,…).
Замечание 1. Мы видим, что в качестве аксиом линейного пространства берутся хорошо известные свойства «геометрических» векторов.
Замечание 2. В некоторых известных учебниках по алгебре используются другие обозначения чисел и векторов.
Основные примеры линейных пространств
1.R1 множество всех векторов на некоторой прямой.
Вдальнейшем такие векторы будем называть векторами-отрезками на прямой. Если в качестве P взять R, то, очевидно, R1 – линейное пространство над полем R.
2.R2, R3 – векторы-отрезки на плоскости и в трехмерном пространстве. Нетрудно видеть, что R2 и R3 линейные пространства над R.
3.Пусть P — произвольное поле. Рассмотрим множество P(n) всех упорядоченных наборов по n элементов поля P:
P(n)= (α1,α2,α3,...,αn)| αi P, i=1,2,..,n .
Набор а=(α1,α2,…,αn) будем называть n-мерным вектором-строкой. Числа i назовем компонентами
вектора а.
Для векторов из P(n), по аналогии с геометрией, естественным образом вводим операции сложения и умножения на число, полагая для любых (α1,α2,…,αn) P(n) и (β1,β2,...,βn) P(n):
(α1,α2,…,αn)+(β1,β2,...,βn)=(α1+β1,α2+b2,...,αn+βn), |
|
(α1,α2,…,αn)= ( α1, α2,…, αn) Р. |
(1) |
Из определения сложения векторов-строк видно, что оно производится покомпонентно. Легко проверить, что P(n) – линейное пространство над P.
Вектор 0=(0,…,0) является нулевым вектором (a+0=a а P(n)), а вектор -a=(-α1,-α2,…,-αn) – противоположным а (т.к. а+(-а)=0).
Линейное пространство P(n) называют n-мерным пространством векторов-строк, или n-мерным арифметическим пространством.
Замечание 3. Иногда через P(n) мы будем обозначать также n-мерное арифметическое пространство векторов-столбцов, отличающееся от P(n) только способом записи векторов.
4.Рассмотрим множество Мn(P) всех матриц n-го порядка с элементами из поля P. Это – линейное пространство над P, где нулевая матрица это матрица, у которой все элементы нули.
5.Рассмотрим множество P[x] всех многочленов от переменной х с коэффициентами из поля P. Нетрудно проверить, что P[x] — линейное пространство над P. Назовем его пространством многочленов.
6.Пусть Pn[x]={ 0xn+…+ n | i P, i=0,1,..,n} множество всех многочленов степени не выше n вместе с
0.Оно является линейным пространством над полем Р. Pn[x] будем называть пространством многочленов степени не выше n.
7.Обозначим через Ф множество всех функций действительного переменного с одной и той же областью определения. Тогда Ф – линейное пространство над R.
Вэтом пространстве можно найти другие линейные пространства, например пространство линейных функций, дифференцируемых функций, непрерывных функций и т.п.
8.Всякое поле является линейным пространством над самим собой.
Некоторые следствия из аксиом линейного пространства
Следствие 1. Пусть L – линейное пространство над полем Р. В L содержится нулевой элемент 0 и а L (-а) L (т.к. L – группа по сложению).
Вдальнейшем нулевой элемент поля Р и линейного пространства L будем обозначать одинаково через
0.Путаницы это обычно не вызывает.
Следствие 2. 0 a=0 a L (в левой части 0 P, в правой 0 L).
Доказательство. Рассмотрим α a, где α — любое число из Р. Имеем: α a=(α+0)a=α a+0 a, откуда 0 a= α a +(-α a)=0.
Следствие 3. α 0=0 α P.
Доказательство. Рассмотрим α a=α(a+0)=α a+α 0; отсюда α 0=0. Следствие 4. α a=0 тогда и только тогда, когда либо α=0, либо а=0.
Доказательство. Достаточность доказана в следствиях 2 и 3.
Докажем необходимость. Пусть α a=0 (2). Предположим, что α 0. Тогда, т.к.α P, то существует α-1 P. Домножая (2) на α-1, получаем:
α-1(α a)=α-1 0. По следствию 2 α-1 0=0, т.е. α-1(α a)=0. (3)
С другой стороны, пользуясь аксиомами 2 и 5 линейного пространства, имеем: α-1(α a)=(α-1α) a=1 a=a.
(4)
Из (3) и (4) следует, что а=0. Следствие доказано.
Следующие утверждения приведем без доказательства (их справедливость легко проверяется).
Следствие 5. (-α) a=-α a α P, a L. Следствие 6. α (-a)=-α a α P, a L. Следствие 7. α (a–b)=α a–α b α P, a,b L.
§ 2. Линейная зависимость векторов
Пусть L – линейное пространство над полем P и a1,a2,…as (1) – некоторое конечное множество векторов из L.
Множество a1,a2,…as будем называть системой векторов.
Если b = α1a1+α2a2+…+αsas, (αi P), то говорят, что вектор b линейно выражается через систему (1), или является линейной комбинацией векторов системы (1).
Как и в аналитической геометрии, в линейном пространстве можно ввести понятия линейно зависимых и линейно независимых систем векторов. Сделаем это двумя способами.
Определение I. Конечная система векторов (1) при s 2 называется линейно зависимой, если хотя бы один ее вектор является линейной комбинацией остальных. В противном случае (т.е. когда ни один ее вектор не является линейной комбинацией остальных), она называется линейно независимой.
Определение II. Конечная система векторов (1) называется линейно зависимой, если существует набор чисел α1,α2,…,αs, αi P, хотя бы одно из которых не равно 0 (такой набор называют ненулевым), что выполняется равенство: α1a1+…+αsas=0 (2).
Из определения II можно получить несколько равносильных определений линейно независимой системы:
Определение 2.
a) система (1) линейно независима, если из (2) следует, что α1=…=αs=0.
b) система (1) линейно независима, если равенство (2) выполняется только при всех αi=0 (i=1,…,s).
c) система (1) линейно независима, если любая нетривиальная линейная комбинация векторов этой системы отлична от 0, т.е. если β1, …,βs – любой ненулевой набор чисел, то β1a1+…βsas 0.
Теорема 1. При s 2 определения линейной зависимости I и II равносильны.
Доказательство.
I) Пусть (1) линейно зависима по определению I. Тогда можно считать, не нарушая общности, что as=α1a1+…+αs-1as-1. Прибавим к обеим частям этого равенства вектор (-as). Получим:
0= α1a1+…+αs-1as-1+(-1) as (3) (так как по следствию 5
(–as) =(-1) as). В равенстве (3) коэффициент (-1) 0, и потому система (1) линейно зависима и по определению
II.
II) Пусть система (1) линейно зависима по определению II, т.е. существует ненулевой набор α1,…,αs, что выполняется (2). Не нарушая общности, можно считать, что αs 0. В (2) к обеим частям прибавим (-αs as). Получим:
α1a1+α2a2+…+αsas- αsas= -αsas, откуда α1a1+…+αs-1as-1= -αsas. |
(4) |
Т.к. αs 0, то существует αs-1 P. Умножим обе части равенства (4) на (-αs-1) и воспользуемся некоторыми аксиомами линейного пространства. Получаем:
(-αs-1) (-αsas)= (-αs-1)( α1a1+…+αs-1as-1), откуда следует: (-αs-1α1) a1+…+(-αs-1) αs-1as-1=as.
Введем обозначения β1= -αs-1α1,…, βs-1=(-αs-1) αs-1. Тогда полученное выше равенство перепишется в виде:
as= β1 a1+…+ βs-1as-1.
Так как s 2, то в правой части будет хотя бы один вектор ai. Мы получили, что система (1) линейно зависима по определению I.
Теорема доказана.
В силу теоремы 1 при необходимости при s 2 мы можем применять любое из данных выше определений линейной зависимости.
Замечание 1. Если система состоит только из одного вектора а1, то к ней применимо только определение
II.
Пусть а1=0; тогда 1а1=0. Т.к. 1 0, то а1=0 линейно зависимая система.
Пусть а1 0; тогда α1а1≠0, при любом α1 0. Значит, ненулевой вектор а1 – линейно независимая
система.
Существуют важные связи между линейной зависимостью системы векторов и ее подсистем.
Теорема 2. Если некоторая подсистема (т.е. часть) конечной системы векторов линейно зависима, то и вся система линейно зависима.
Доказательство этой теоремы нетрудно провести самостоятельно. Его можно найти в любом учебнике по алгебре или аналитической геометрии.
Следствие 1. Все подсистемы линейно независимой системы линейно независимы. Получается из теоремы 2 методом от противного.
Замечание 2. Нетрудно видеть, что у линейно зависимых систем подсистемы могут быть как линейно
зависимые, так и линейно независимые. |
|
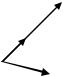
Пример. На рис.1 a1, a2, a3 линейно зависимая система. |
|
a1, a2 ее линейно зависимая подсистема, |
Рис.1 |
a1, a3 ее линейно независимая подсистема. |
|
a2
a1
a3
Рис. 1
Следствие 2. Если система содержит 0 или два пропорциональных (равных) вектора, то она линейно зависима (так как подсистема из 0 или двух пропорциональных векторов линейно зависима).
§ 3. Максимальные линейно независимые подсистемы
Определение 3. Пусть a1, a2,…,ak,…. (1) – конечная или бесконечная система векторов линейного пространства L. Ее конечная подсистема ai1, ai2, …, air (2) называется базисом системы (1) или максимальной линейно независимой подсистемой этой системы, если выполняются следующие два условия:
1) подсистема (2) линейно независима;
2) если к подсистеме (2) приписать любой вектор аj системы (1), то получаем линейно зависимую
систему ai1, ai2, …, air, aj (3).
Пример 1. В пространстве Рn[x] рассмотрим систему многочленов 1,x1, …, xn (4). Докажем, что (4) линейно независима. Пусть α0, α1,…, αn – такие числа из Р, что α01+α1x+...+αnxn=0. Тогда по определению равенства многочленов α0=α1=…=αn=0. Значит, система многочленов (4) линейно независима.
Докажем теперь, что система (4) – базис линейного пространства Pn[x].
Для любого f(x) Pn[x] имеем: f(x)=β0xn+…+βn 1 Pn[x]; следовательно, f(x) является линейной комбинацией векторов (4); тогда система 1,x1, …, xn,f(x) линейно зависима (по определению I). Таким образом, (4) – базис линейного пространства Pn[x].
Пример 2. На рис. 1 a1, a3 и a2, a3 – базисы системы векторов a1,a2,a3.
Теорема 3. Подсистема (2) ai1,…, air конечной или бесконечной системы (1) a1, a2,…,as,… является максимальной линейно независимой подсистемой (базисом) системы (1) тогда и только тогда, когда
а) (2) линейно независима; б) любой вектор из (1) линейно выражается через (2).
Необходимость. Пусть (2) – максимальная линейно независимая подсистема системы (1). Тогда выполняются два условия из определения 3:
1)(2) линейно независима.
2)Для любого вектора aj из (1) система ai1,…, ais,aj (5) линейно зависима. Надо доказать, что выполняются утверждения а) и б).
Условие а) совпадает с 1); следовательно, а) выполняется.
Далее, в силу 2) существует ненулевой набор α1,...,αr,β P (6) такой, что α1ai1+…+αrair+βaj=0 (7). Докажем, что β 0 (8). Предположим, что β=0 (9). Тогда из (7) получаем: α1ai1+…+αrair=0 (10). Из того, что набор (6) ненулевой, а β=0 следует, что α1,...,αr ненулевой набор. А тогда из (10) вытекает, что (2) линейно зависима, что противоречит условию а). Этим доказано (8).

Прибавив к обеим частям равенств (7) вектор (-βaj), получим: -βaj= α1ai1+…+αrair. Так как β 0, то
существует β-1Р; умножим обе части последнего равенства на β-1: (β-1α1)ai1+…+ (β-1αr)air=aj. Введем
обозначения: (β-1α1)= 1,…, (β-1αr)= r; таким образом, мы получили: 1ai1+…+ r air=aj; следовательно, доказана выполнимость условия б).
Необходимость доказана.
Достаточность. Пусть выполняются условия а) и б) из теоремы 3. Нужно доказать, что выполняются условия 1) и 2) из определения 3.
Так как условие а) совпадает с условием 1), то 1) выполняется.
Докажем, что выполняется 2). По условию б), любой вектор aj (1) линейно выражается через (2). Следовательно, (5) линейно зависима (по определению 1), т.е. 2) выполняется.
Теорема доказана.
Замечание. Не в любом линейном пространстве существует базис. Например, нет базиса в пространстве Р[x] (в противном случае, степени всех многочленов из Р[x] были бы, как следует из пункта б) теоремы 3, ограничены в совокупности).
§ 4. Основная теорема о линейной зависимости. Ее следствия
Определение 4. Пусть даны две конечные системы векторов линейного пространства L:a1,a2,…,al (1) и
b1,b2,…,bs (2).
Если каждый вектор системы (1) линейно выражается через (2), то будем говорить, что система (1)
линейно выражается через (2). Примеры:
1.Любая подсистема системы a1,…,ai,…,ak линейно выражается через всю систему, т.к.
ai=0 a1+…+1 ai+…+0 ak.
2. Любая система векторов-отрезков из R2 линейно выражается через систему, состоящую из двух неколлинеарных векторов плоскости.
Определение 5. Если две конечные системы векторов линейно выражаются друг через друга, то они называются эквивалентными.
Замечание 1. Число векторов в двух эквивалентных системах может быть разным, что видно из следующих примеров.
Примеры:
3.Каждая система эквивалентна своему базису (это следует из теоремы 3 и примера 1).
4.Любые две системы векторов-отрезков из R2, в каждой из которых есть два неколлинеарных вектора, эквивалентны.
Следующая теорема является одним из важнейших утверждений теории линейных пространств. Основная теорема о линейной зависимости. Пусть в линейном пространстве L над полем P заданы две
системы векторов:
a1,a2,…,al (1) и b1,b2,…,bs (2), причем (1) линейно независима и линейно выражается через (2). Тогда l s (3). Доказательство. Нам надо доказать неравенство (3). Предположим противное, пусть l>s (4).
По условию каждый вектор ai из (1) линейно выражается через систему (2):
a1=α11b1+α12b2+…+α1sbs a2=α21b1+a22b2+…+α2sbs
…………………... (5)
al=αl1b1+αl2b2+…+αlsbs.
Составим следующее уравнение: x1a1+x2a2+…+x1al=0 (6), где xi— неизвестные, принимающие значения из поля Р (i=1,…,s).
Умножим каждое из равенств (5), соответственно на x1,x2,…,xl, подставим в (6) и соберем вместе слагаемые, содержащие b1, затем b2 и, наконец, bs. Получим:
x1a1+…+xlal = (α11x1+α21x2+ … +αl1xl)b1 |
+ (α12x1+α22x2+ … +αl2xl)b2 + …+(α1sx1+α2sx2+…+αlsxl)bs=0. |
(7) |
|
Постараемся найти ненулевое решение |
уравнения (6). Для этого приравняем в (7) к нулю все |
коэффициенты при bi (i=1, 2,…,s) и составим следующую систему уравнений: |
|
α11x1+α21x2+ … +αl1xl=0 |
|
α12x1+α22x2+…+αl2xl=0 |
(8) |
……………………. |
|
α1sx1+α2sx2+…+αlsxl=0.
(8)однородная система s уравнений относительно неизвестных x1,…,xl. Она всегда совместна.
Всилу неравенства (4) в этой системе число неизвестных больше числа уравнений, и потому, как следует из метода Гаусса, она приводится к трапецеидальному виду. Значит, существуют ненулевые
решения системы (8). Обозначим одно из них через x10,x20,…,xl0 (9), xi0 P (i=1, 2,…s).
Подставив числа (9) в левую часть (7), получим: x10a1+x20a2+…+xl0al=0 b1+0 b2+…+0 bs=0. (10)
Итак, (9) – ненулевое решение уравнения (6). Поэтому система (1) линейно зависима, а это противоречит условию. Следовательно, наше предположение (4) неверно и l s.
Теорема доказана.
Следствия из основной теоремы о линейной зависимости Следствие 1. Две конечные эквивалентные линейно независимые системы векторов состоят из
одинакового числа векторов.
Доказательство. Пусть системы векторов (1) и (2) эквивалентны и линейно независимы. Для доказательства применим два раза основную теорему.
Т.к. система (2) линейно независима и линейно выражается через (1), то по основной теореме l s (11).
С другой стороны, (1) линейно независима и линейно выражается через (2), и по основной теореме s l (12).
Из (11) и (12) следует, что s=l. Утверждение доказано.
Следствие 2. Если в некоторой системе векторов a1,…,as,… (13) (конечной или бесконечной) существует два базиса, то они состоят из одинакового количества векторов.
Доказательство. Пусть ai1,…,ail (14) и aj1,..ajk (15) – базисы системы (13). Покажем, что они эквивалентны.
По теореме 3 каждый вектор системы (13) линейно выражается через ее базис (15), в частности, любой вектор системы (14) линейно выражается через систему (15). Аналогично система (15) линейно выражается через (14). Значит, системы (14) и (15) эквивалентны и по следствию 1 имеем: l=k.
Утверждение доказано.
Определение 6. Число векторов в произвольном базисе конечной (бесконечной) системы векторов называют рангом этой системы (если базисов нет, то ранга системы не существует).
В силу следствия 2, если система (13) имеет хотя бы один базис, ее ранг единственен.
Замечание 2. Если система состоит только из нулевых векторов, то полагаем, что ее ранг равен 0. Пользуясь понятием ранга, можно усилить основную теорему.
Следствие 3. Даны две конечные системы векторов (1) и (2), причем (1) линейно выражается через (2). Тогда ранг системы (1) не превосходит ранга системы (2).
Доказательство. Обозначим ранг системы (1) через r1, ранг системы (2) — через r2. Если r1=0, то утверждение верно.
Пусть r1 0. Тогда и r2 0, т.к. (1) линейно выражается через (2). Значит, в системах (1) и (2) существуют базисы.
Пусть a1,…,ar1 (16) – базис системы (1) и b1,…,br2 (17) – базис системы (2). Они линейно независимы по определению базиса.
Далее, (16) линейно выражается через (1), как часть системы (1). Система (1) линейно выражается через (2), а (2) линейно выражается через свой базис (17). Значит, (16) линейно выражается через (17).
Т.к. (16) линейно независима, то к паре систем (16), (17) можно применить основную теорему. По этой
теореме r1 r2. Утверждение доказано.
Следствие 4. Две конечные эквивалентные системы векторов имеют одинаковые ранги. Для доказательства этого утверждения надо два раза применить следствие 3.
Замечание 3. Отметим, что ранг линейно независимой системы векторов равен числу ее векторов (ибо в линейно независимой системе ее единственный базис совпадает с самой системой). Поэтому следствие 1— это частный случай следствия 4. Но без доказательства этого частного случая мы не смогли бы доказать следствие 2, ввести понятие ранга системы векторов и получить следствие 4.
§ 5. Конечномерные линейные пространства
Определение 7. Линейное пространство L над полем P называется конечномерным, если в L существует хотя бы один базис.
Основные примеры конечномерных линейных пространств:
1.Векторы-отрезки на прямой, плоскости и в пространстве (линейные пространства R1, R2, R3).
2.n-мерное арифметическое пространство P(n). Покажем, что в P(n) существует следующий базис: e1=(1,0,…,0)
e2=(0,1,…,0) (1)
……….
en=(0,0,…1).
Докажем сначала, что (1) – линейно независимая система. Составим уравнение x1e1+x2e2+…+xnen=0 (2).
Используя вид векторов (1), уравнение (2) перепишем так: x1(1,0,…,0)+x2(0,1,…,0)+…+xn(0,0,…,1)=(x1, x2, …,xn)=(0,0,…,0).
По определению равенства векторов-строк отсюда следует:
x1=0, x2=0,…, xn=0 (3). Следовательно, (1) – линейно независимая система. Докажем, что (1) – базис пространства P(n), пользуясь теоремой 3 о базисах.
Для любого a=(α1,α2,…,αn) Pn имеем:
а=(α1,α2,…,αn)=(α1,0,…,0)+(0,α2,…,0)+(0,0,…,αn)= 1e1+ 2e2+…+ nen.
Значит, любой вектор пространства P(n) линейно выражается через (1). Следовательно,(1) – базис пространства P(n), и потому P(n) – конечномерное линейное пространство.
3. Линейное пространство Pn[x]={α0xn+...+αn | αi P}.
Нетрудно проверить, что базисом пространства Pn[x] является система многочленов 1,x,…,xn. Значит, Pn
[x]– конечномерное линейное пространство.
4.Линейное пространство Mn(P). Можно проверить, что множество матриц вида Eij, в которых единственный ненулевой элемент 1 стоит на пересечении i-й строки и j-го столбца (i,j=1,…,n), составляют базис Mn(P).
Следствия из основной теоремы о линейной зависимости для конечномерных линейных пространств
Наряду со следствиями из основной теоремы о линейной зависимости 1–4, из этой теоремы можно получить еще несколько важных утверждений.
Следствие 5. Любые два базиса конечномерного линейного пространства состоят из одинакового числа векторов.
Это утверждение – частный случай следствия 2 из основной теоремы о линейной зависимости, примененного ко всему линейному пространству.
Определение 8. Число векторов в произвольном базисе конечномерного линейного пространства L называют размерностью этого пространства и обозначают dim L.
В силу следствия 5 всякое конечномерное линейное пространство имеет единственную размерность. Определение 9. Если линейное пространство L имеет размерность n, то его называют n-мерным
линейным пространством. Примеры:
1.dim R1=1;
2.dimR2=2;
3.dimP(n)=n, т.е. P(n) – n–мерное линейное пространство, т.к. выше, в примере 2 показано, что (1) – базис
P(n);
4.dimPn[x]=(n+1), ибо, как нетрудно проверить, 1,x,x2,…,xn базис из n+1 векторов этого пространства;
5.dimMn(P)=n2, ибо матриц вида Eij, указанных в примере 4, ровно n2.
Следствие 6. В n-мерном линейном пространстве L любые n+1 векторов a1,a2,…,an+1 (3) составляют линейно зависимую систему.
Доказательство. По определению размерности пространства в L существует базис из n векторов: e1,e2,…,en (4). Рассмотрим пару систем (3) и (4).
Предположим, что (3) линейно независима. Т.к. (4) – базис L, то любой вектор пространства L линейно выражается через (4) (по теореме 3 из §3). В частности, система (3) линейно выражается через (4). По предположению (3) линейно независима; тогда к паре систем (3) и (4) можно применить основную теорему о линейной зависимости. Получаем: n+1 n, что невозможно. Противоречие доказывает, что (3) линейно зависима.
Следствие доказано.
Замечание 1. Из следствия 6 и теоремы 2 из §2 получаем, что в n-мерном линейном пространстве любая конечная система векторов, содержащая больше n векторов, линейно зависима.
Из этого замечания вытекает
Следствие 7. В n-мерном линейном пространстве любая линейно независимая система содержит не более n векторов.
Замечание 2. С помощью этого утверждения можно установить, что некоторые линейные пространства не являются конечномерными.
Пример. Рассмотрим пространство многочленов P[x] и докажем, что оно не является конечномерным. Предположим, что dim P[x]=m, m N. Рассмотрим 1, x,…, xm – множество из (m+1) векторов из P[x]. Эта система векторов, как отмечено выше, линейно независима, что противоречит предположению, что размерность P[x] равна m.
Нетрудно проверить (используя P[x]), что конечномерными линейными пространствами не являются пространства всех функций действительной переменной, пространства непрерывных функций и т.д.
Следствие 8. Любую конечную линейно независимую систему векторов a1, a2,…,ak (5) конечномерного линейного пространства L можно дополнить до базиса этого пространства.
Доказательство. Пусть n=dim L. Рассмотрим два возможных случая.
1.Если k=n, тогда a1, a2,…,ak – линейно независимая система из n векторов. В силу следствия 7, для любого b L система a1, a2,…,ak, b линейно зависима, т.е. (5) – базис L.
2.Пусть k n. Тогда система (5) не является базисом L, а значит, существует вектор ak+1 L, что a1, a2,…,ak, ak+1 (6) линейно независимая система. Если (k+1)<n, то также приписываем ak+2, и так далее.
В силу следствия 7 этот процесс заканчивается через конечное число шагов. Получаем базис a1, a2,…,ak, ak+1,…,an линейного пространства L, содержащий (5).
Следствие доказано.
Из следствия 8 вытекает
Следствие 9. Любой ненулевой вектор конечномерного линейного пространства L содержится в некотором базисе L (т.к. такой вектор является линейно независимой системой).
Отсюда следует, если Р – бесконечное поле, то в конечномерном линейном пространстве над полем Р существует бесконечно много базисов (т.к. в L бесконечно много векторов вида a, a 0, P\0).
§ 6. Изоморфизм линейных пространств
Определение 10. Два линейных пространства L и L`над одним полем Р называются изоморфными, если существует биекция : L L`, удовлетворяющая следующим условиям:
1.(a+b)= (a)+ (b) a, b L,
2.( a)= (a) P, a L.
Само такое отображение называется изоморфизмом или изоморфным отображением.
Свойства изоморфизмов.
1. При изоморфизме нулевой вектор переходит в нулевой.
Доказательство. Пусть a L и : L L` – изоморфизм. Так как a=a+0, то (a)= (a+0)= (a)+ (0).
(1)
Т.к. (L)=L` то из последнего равенства видно, что (0) (обозначим его через 0`) – это нулевой вектор из
L`.
2. При изоморфизме линейно зависимая система переходит в линейно зависимую систему. Доказательство. Пусть a1, a2,…,as (2) – некоторая линейно зависимая система из L. Тогда существует
ненулевой набор чисел 1,…, s (3) из Р, что 1a1+…+ sas=0. Подвергнем обе части этого равенства изоморфному отображению . Учитывая определение изоморфизма, получим:
1 (a1)+…+ s (as)= (0)=0` (мы использовали свойство 1). Т.к. набор (3) ненулевой, то из последнего равенства следует, что ( 1),…, ( s) – линейно зависимая система.
3. Если : L L` изоморфизм, то -1: L` L – тоже изоморфизм.
Доказательство. Так как – биекция, то существует биекция -1: L` L. Требуется доказать, что если a`,
b` L`, то |
|
-1(a`+b`)= -1(a`)+ -1(b`). |
(4) |
Так как – биекция, то a`= (a), b`= (b), для некоторых a, b L. |
|
Имеем: -1(a`+b`)= -1( (a)+ (b)). |
(5) |
Так как — изоморфизм, то a`+b`= (a)+ (b) = (a+b). Отсюда следует:
a+b= -1( (a+b))= -1( (a)+ (b)). |
(6) |
Из (5) и (6) имеем -1(a`+b`)=a+b= -1(a`)+ -1(b`).
Аналогично проверяется, что -1( a`)= -1(a`). Итак, -1 – изоморфизм.
Свойство доказано.
4. При изоморфизме линейно независимая система переходит в линейно независимую систему. Доказательство. Пусть : L L` изоморфизм и a1, a2,…,as (2) – линейно независимая система. Требуется
доказать, что (a1), (a2),…, (as) (7) также линейно независима.
Предположим, что (7) линейно зависима. Тогда при отображении -1 она переходит в систему a1, …,as.
По свойству 3 -1 – изоморфизм, а тогда по свойству 2 система (2) будет также линейно зависимой, что противоречит условию. Следовательно, наше предположение неверно.
Свойство доказано.
5. При изоморфизме базис любой системы векторов переходит в базис системы ее образов. Доказательство. Пусть a1, a2,…,as,… (8) – конечная или бесконечная система векторов линейного
пространства L, : L L` – изоморфизм. Пусть система (8) имеет базис ai1, …,air (9). Покажем, что система
(a1),…, (aк),… (10) имеет базис (ai1), …, (air) (11).
Так как (9) линейно независима, то по свойству 4 система (11) линейно независима. Припишем к (11) любой вектор из (10); получим: (ai1), …, (air), (aj) (12). Рассмотрим систему ai1, …,air, aj (13). Она линейно зависима, так как (9) – базис системы (8). Но (13) при изоморфизме переходит в (12). Так как (13) линейно зависима, то по свойству 2 система (12) тоже линейно зависима. Значит, (11) есть базис системы (10).
Применяя свойство 5 ко всему конечномерному линейному пространству L, получим
Утверждение 1. Пусть L – n-мерное линейное пространство над полем P, : L L` изоморфизм. Тогда L` – также конечномерное пространство и dim L`= dim L = n.
В частности, справедливо Утверждение 2. Если конечномерные линейные пространства изоморфны, то их размерности равны.
Замечание. В §7 будет установлена справедливость и обратного к этому утверждения.
§ 7. Координаты вектора
Пусть L – конечномерное линейное пространство над полем Р и e1,…,en (1) – некоторый базис L.
В дальнейшем базис всегда будем считать упорядоченным (т.е. если в нем поменять местами некоторые векторы, то получим уже другой базис).
Определение 11. Пусть а L. Выразим вектор а через базис (1), т.е. a= 1e1+…+ nen (2), i P (i=1,…,n). Столбец ( 1,…, n)т (3) называется координатным столбцом вектора а в базисе (1).
Координатный столбец вектора а в базисе е обозначается также через [a], [a]e или [ 1,.., n].
Как и в аналитической геометрии, доказывается единственность выражения вектора через базис, т.е. единственность координатного столбца вектора в данном базисе.
Замечание 1. В некоторых учебниках вместо координатных столбцов рассматривают координатные строки (например, в книге [1]). В таком случае получаемые там формулы на языке координатных столбцов выглядят иначе.
Теорема 4. Пусть L – n-мерное линейное пространство над полем Р и (1) – некоторый базис L. Рассмотрим отображение : a ( 1,…, n)т, ставящее в соответствие любому вектору а из L его координатный столбец в базисе (1). Тогда – изоморфизм пространств L и P(n) (P(n) – n-мерное арифметическое пространство векторов-столбцов).
Доказательство. Отображение однозначно в силу единственности координат вектора. Легко проверяется, что – биекция и ( a)= (a), (a)+ (b)= (a+b). Значит изоморфизм.
Теорема доказана.
Следствие 1. Система векторов a1,a2,…,as конечномерного линейного пространства L тогда и только тогда линейно зависима, когда линейно зависима система, состоящая из координатных столбцов этих векторов в некотором базисе пространства L.
Справедливость этого утверждения вытекает из теоремы 1 и второго и четвертого свойств изоморфизма. Замечание 2. Следствие 1 позволяет изучение вопроса о линейной зависимости систем векторов в
конечномерном линейном пространстве свести к решению такого же вопроса для столбцов некоторой матрицы.
Теорема 5 (критерий изоморфизма конечномерных линейных пространств). Два конечномерных линейных пространства L и L` над одним полем P тогда и только тогда изоморфны, когда имеют одну и ту же размерность.
Необходимость. Пусть L L` В силу утверждения 2 из §6 размерность L совпадает с размерностью L1.
Достаточность. Пусть dim L = dim L`= n. Тогда в силу теоремы 4 имеем: L P(n) |
и L` P(n). Отсюда |
|
нетрудно получить, что L L`. |
|
|
Теорема доказана. |
|
|
Примечание. В дальнейшем через Ln мы часто будет обозначать n-мерное линейное пространство. |
||
§ 8. Матрица перехода |
|
|
Определение 12. Пусть в линейном пространстве Ln |
заданы два базиса: |
|
е= (е1, … еn) и e`=(e1`,…,e`n) (старый и новый). |
|
|
Разложим векторы базиса е` по базису е: |
|
|
e`1=t11e1+…+tn1en |
|
|
………………….. |
(1) |
|
e`n=t1ne1+…+tnnen.
Матрицу
t11………t1n
Т= ……………
tn1………tnn
называют матрицей перехода от базиса е к базису е`.
Отметим, что равенства (1) в матричном виде удобно записать так: е`=еТ (2). Это равенство равносильно определению матрицы перехода.
Замечание 1. Сформулируем правило построения матрицы перехода: для построения матрицы перехода от базиса е к базису е` нужно для всех векторов ej` нового базиса e` найти их координатные столбцы в старом базисе е и записать их в качестве соответствующих столбцов матрицы Т.

Замечание 2. В книге [1] матрица перехода составляется по строкам (из координатных строк векторов нового базиса в старом).
Теорема 6. Матрица перехода от одного базиса n-мерного линейного пространства Ln над полем P к другому его базису является невырожденной матрицей n-го порядка с элементами из поля Р.
Доказательство. Пусть Т матрица перехода от базиса е к базису e`. Столбцы матрицы Т по определению 12 это координатные столбцы векторов базиса е` в базисе е. Так как е` линейно независимая система, то по следствию 1 теоремы 4 столбцы матрицы Т линейно независимы, и потому |T|≠0.
Теорема доказана.
Верно и обратное утверждение.
Теорема 7. Любая невырожденная квадратная матрица n-го порядка с элементами из поля Р служит матрицей перехода от одного базиса n-мерного линейного пространства Ln над полем Р к некоторому другому базису Ln.
Доказательство. Пусть даны базис е=(е1, …, еn) линейного пространства L и невырожденная квадратная матрица
Т= t11………t1n
……………
tn1………tnn
n-го порядка с элементами из поля Р. В линейном пространстве Ln рассмотрим упорядоченную систему векторов e`=(e1`,…,e`n), для которых столбцы матрицы Т являются координатными столбцами в базисе е.
Система векторов е` состоит из n векторов и является в силу следствия 1 теоремы 4 линейно независимой, так как у невырожденной матрицы Т столбцы линейно независимы. Поэтому эта система – базис линейного пространства Ln, причем в силу выбора векторов системы e` выполняется равенство e`=eT. Это означает, что Т– матрица перехода от базиса е к базису e`.
Теорема доказана.
Связь координат вектора а в разных базисах
Пусть в линейном пространстве Ln заданы базисы е=(е1, … еn) и e`=(e1`,…,e`n) с матрицей перехода Т от базиса е к базису е`, т.е. верно (2). Вектор а имеет в базисах е и е` координаты [a]e=( 1,…, n)T и [a]e`=( 1`,…,
n`)T, т.е. a=e[a]e и a=e`[a]e`.
Тогда, с одной стороны, a=e[a]e, а с другой a=e`[a]e`=(eT)[a]e`=e(T[a]e`) (мы использовали равенство (2)). Из этих равенств получим: a=e[a]e=e(T[a]e`). Отсюда в силу единственности разложения вектора по базису
е вытекает равенство [a]e=Т[a]e` (3), или
1 |
1` |
|
2 |
2` |
|
… = T |
… |
(4) |
n |
n` . |
|
Соотношения (3) и (4) называют формулами преобразования координат при изменении базиса линейного пространства. Они выражают старые координаты вектора через новые. Эти формулы можно разрешить относительно новых координат вектора, умножив (4) слева на Т-1 (такая матрица существует, так как Т невырожденная матрица).
Тогда получим: [a]e`=T-1[a]e. По этой формуле, зная координаты вектора в старом базисе е линейного пространства Ln, можно найти его координаты в новом базисе, e`.
§ 9. Подпространства линейного пространства
Определение 13. Пусть L – линейное пространство над полем Р и H L. Если H также является линейным пространством над Р относительно тех же операций, что и L, то H называют подпространством линейного пространства L.
Утверждение 1. Подмножество Н линейного пространства L над полем Р является подпространством L, если выполняются следующие условия:
1.h1+h2 H для любых h1, h2 H;
2.h H для любого h H и P.
Доказательство. Если в Н выполняются условия 1 и 2, то в Н заданы сложение и умножение на элементы поля Р. Выполнимость большинства аксиом линейного пространства для Н следует из их справедливости для L. Проверим некоторые из них:
а) 0 h=0 H (в силу условия 2);
b) h H имеем: (-h)=(-1)h H (в силу условия 2).
Утверждение доказано.
Примеры:
1.Подпространствами любого линейного пространства L являются 0 и L.
2.R1– подпространство пространства R2 векторов-отрезков на плоскости.
3.Пространство функций действительной переменной имеет, в частности, следующие подпространства:
а) линейных функций вида ax+b;
б) непрерывных функций; в) дифференцируемых функций.
Один универсальный способ выделения подпространств любого линейного пространства связан с понятием линейной оболочки.
Определение 14. Пусть a1,…as (1) – произвольная конечная система векторов линейного пространства L. Назовем линейной оболочкой этой системы множество { 1a1+…+ sas | iP} = <a1,…,as>. Линейную оболочку системы (1) обозначают также L(a1,…,as).
Теорема 8. Линейная оболочка Н любой конечной системы векторов (1) линейного пространства L является конечномерным подпространством линейного пространства L. Базис системы (1) является и базисом Н, и размерность Н равна рангу системы (1).
Доказательство. Пусть Н=<a1,….,as>. Из определения линейной оболочки легко следует выполнимость условий 1 и 2 утверждения 1. В силу этого утверждения, Н – подпространство линейного пространства L. Пусть ai1,….,air (2) – базис системы (1). Тогда имеем: любой вектор h H линейно выражается через (1) – по определению линейной оболочки, а (1) линейно выражается через свой базис (2). Так как (2) – линейно независимая система, то она является базисом Н. Но число векторов в (2) равно рангу системы (1). Значит, dimH=r.
Теорема доказана.
Замечание 1. Если Н – конечномерное подпространство линейного пространства L и h1,…,hm – базис Н, то легко видеть, что H=<h1,..,hm>. Значит, линейные оболочки – это универсальный способ построения конечномерных подпространств линейных пространств.
Определение 15. Пусть А и В – два подпространства линейного пространства L над полем Р. Назовем их суммой А+В следующее множество: А+В={a+b| a A, b B}.
Пример. R2 является суммой подпространств OX (векторы оси OX) и OY. Легко доказать следующее
Утверждение 2. Сумма и пересечение двух подпространств линейного пространства L являются подпространствами L (достаточно проверить выполнимость условий 1 и 2 утверждения 1).
Справедлива
Теорема 9. Если А и В – два конечномерных подпространства линейного пространства L, то dim(A+B)=dimA+ dimB–dim A B.
Доказательство этой теоремы можно посмотреть, например, в [1].
Замечание 2. Пусть А и В – два конечномерных подпространства линейного пространства L. Для нахождения их суммы А+В удобно использовать задание А и В линейными оболочками. Пусть А=<a1,…,am>, В=<b1,…,bs>. Тогда нетрудно показать, что А+В= <a1,…,am, b1,…,bs>. Размерность А+В по доказанной выше теореме 7 равна рангу системы a1,…,am, b1,…,bs. Поэтому, если найти базис этой системы, то найдем и dim (A+B).
