
Высшая математика. Экзамен. 1-2 семестр / 2 сем / линейные преобразования линейных пространств
.pdf
ГЛАВА 10. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ЛИНЕЙНЫХ ПРОСТРАНСТВ § 1. Линейные отображения линейных пространств
Определение 1. Отображение линейного пространства L в линейное простанство L` называется
линейным отображением, если для любых a, b L (a+b)= (a)+ (b) и P и а L ( a)= (a).
Лемма 1. Пусть : L L` – линейное отображение конечномерного линейного пространства L в линейное пространство L`. Тогда образ любого вектора из L при отображении однозначно определяется образами векторов некоторого базиса e1,…,en (1) пространства L при этом отображении.
Доказательство. Пусть a L. Тогда a= 1е1+…+ nеn (2). Из определения линейного отображения имеем:(a)= ( 1e1)+…+ ( nen)= 1 (e1)+…+ n (en) (3). Из (3) видно, что если известны векторы (e1),…, (en), то однозначно находится (a) (ибо координаты вектора а в базисе (1) единственны).
Лемма доказана.
Следствие. Если два линейных отображения и n-мерного линейного пространства L в L` над Р совпадают на некотором базисе (1) линейного пространства L, то = .
Доказательство. Пусть и – линейные отображения L L`, удовлетворяющие условию: (ei)= (ei) (i=1,2,..,n). Тогда в силу леммы 1 для любого а L имеем: (а)= (а), откуда = (по определению равенства отображений).
Следствие доказано.
Лемма 2. Пусть L – n-мерное линейное пространство с базисом (1); L` – любое линейное пространство над тем же полем Р и c1,…, cn – произвольные векторы, принадлежащие L`. Тогда существует линейное отображение : L L` такое, что (ei)=сi (4) для любого i=1,2..,n, причем такое отображение единственно.
Доказательство. Единственность вытекает из следствия леммы 1.
Докажем существование такого отображения. Так как (1) базис, то для каждого a L справедливо
равенство
a
n iei
i 1
(2) при некоторых αi P. По определению полагаем:
n(a) ici
i 1
, т.е. в (2) все ei
заменили на ci. Отметим, что ( L L`. Докажем линейность .
a
) L` и однозначно определяется вектором
a
, т.е. – отображение
Если P, то вектор
n
Далее, если b i
i 1
a
ei ,
n |
|
i i |
|
|
|
|
|
|
e |
, |
|
i 1 |
|
|
|
то |
(b |
||
и по определению
|
n |
i i |
|
) |
|
|
|
|
c |
. Так как |
|
|
i 1 |
|
|
имеем: ( a) |
n |
|
i |
|
( |
||
|
|
||
|
i 1 |
|
|
n
a b ( i i )ei ,то
i 1
)c |
i |
|
|
|
по
(a) .
определению отображения
|
n |
n |
n |
(a+b)= (a)+ (b) |
a, |
b L. |
имеем: |
(a b) ( i i )ci ici ici (a) (b) . Таким образом, |
|||||
|
i 1 |
i 1 |
i 1 |
|
|
|
Следовательно – линейное отображение.
Осталось проверить справедливость равенства (4).
Так как ei=0e1+…+1 ei+…+0en, то по определению отображения : (ei)=0c1+…+1 ci+…+0cn=ci, т.е. – искомое отображение.
Лемма доказана.
Замечание 1. Из леммы 2 видно, что для задания линейного отображения n-мерного линейного пространства L в L` достаточно задать n векторов из L`.
§2. Линейные преобразования линейных пространств
Определение 2. Линейное отображение : L L назовем линейным преобразованием L (т.е. линейное преобразование L – это линейное отображение L в себя).
Примеры линейных преобразований:
I. Линейными преобразованиями пространства R2 являются:
1.Проектирование на некоторую ось;
2.Преобразование растяжения ( (a)= a a R2);
3.Поворот плоскости на некоторый угол;
4.Симметрия относительно оси, относительно точки; II. Дифференцирование пространства многочленов P[x]
(f(x) f ´(x)).
Для описания линейных преобразований конечномерных линейных пространств удобно использовать матрицы.
Определение 3. Пусть – линейное преобразование конечномерного линейного пространства L, е=(e1,…,en) – некоторый базис этого пространства. Матрица А, столбцы которой являются координатными столбцами векторов (е1),…, (еn) в базисе e, называется матрицей линейного преобразования в базисе е.
Чтобы составить матрицу А линейного преобразования в базисе е, нужно найти векторы (е1),…, (еn) и выразить каждый из них через базис е:
(e1)= 11е1+…+ n1еn
............................. (5)

(en)= 1nе1+…+ nnеn.
Тогда
11…….. 1n
A= ……………
n1…….. nn
.
Замечание 1. Если ввести обозначение (е)=( (е1),…, (еn)), то равенства (5) перепишутся в виде:(е)=еА. Это матричная форма определения матрицы линейного преобразования.
Теорема 1. Пусть – линейное преобразование n-мерного линейного пространства L над Р, е=(e1,…en) – базис L, А – матрица преобразования в базисе e. Тогда отображение w: A – биекция множества F всех линейных преобразований пространства L на множество Mn(P) всех матриц n-го порядка с элементами из поля Р.
Доказательство. Из определения матрицы линейного преобразования видно, что в базисе е имеет единственную матрицу А. Потому w: A – отображение множества F в множество Mn(P). Далее, если А Mn(P), то обозначим через c1,…,cn векторы из L, координатами которых в базисе е являются столбцы матрицы А. По лемме 2 существует такое линейное преобразование F, что (ei)=ci (i=1,…, n). Тогда А – матрица линейного преобразования в базисе е, т.е. w: A. Значит, w – сюръекция.
Осталось доказать, что w инъекция. Если , F и w( )=w( )=А, то (ei)= (ei) (i=1,…,n). По лемме 1= . Этим доказано, что w биекция.
Теорема доказана.
Следствие. Любая матрица n-го порядка с элементами из поля Р является матрицей некоторого линейного преобразования произвольного n-мерного линейного пространства над Р (это утверждение доказано в ходе доказательства теоремы 1).
Замечание 2. Теорема 1 означает, что изучение линейных преобразований конечномерных линейных пространств и квадратных матриц над Р – это близкие задачи.
Координаты образа вектора при линейном преобразовании
Пусть – линейное преобразование n-мерного линейного пространства L и е=(е1,…,en) – некоторый базис L. Решим следующую задачу: по координатному столбцу [a] вектора а из L в базисе е найти
координатный столбец [ (a)] вектора (а) в том же базисе. Из
n
преобразование, получаем: (a) i (ei ) (e) [a] (6), где
i 1
|
n |
i |
|
i |
|
|
|
||
a |
|
|
e |
, учитывая то, что – линейное |
|
i 1 |
|
|
|
(е)=( (е1),…, (еn)). Пусть А – матрица
преобразования в базисе е, т.е. (е)=еА. Подставляя (е) в равенство (6), получаем: (а)=(еA)[a]=e(A[a]). Отсюда следует
Утверждение 1. [ (а)]=A[a]. (7)
Поставленная выше задача решена.
Замечание 3. Равенство (7) легко запомнить: чтобы найти координатный столбец вектора (а), надо вместо в эту запись поставить его матрицу А, вместо вектора а – его координатный столбец [a] – все в базисе е – и получим А[a] координатный столбец (а) в базисе е.
Замечание 4. Из справедливости равенства (7) для некоторой матрицы А и любого вектора а L в базисе е нетрудно заключить, что А – матрица линейного преобразования в этом базисе. Для этого надо из равенства (7) найти столбцы [ (е1)], …,[ (en)]. Учитывая, что[e1]=[1, 0, …,0],…,[en]=[0,0,…,1], получим, что это столбцы матрицы А, а тогда, по определению матрицы линейного преобразования, матрица А и является матрицей в базисе е. Другими словами, справедливость равенства (7) для любого a L равносильна определению матрицы линейного преобразования .
§ 3. Связь матриц линейного преобразования в разных базисах конечномерного линейного пространства
Лемма 3. Если С и D – две матрицы n-го порядка над Р, e некоторый базис линейного пространства L над Р и еС=eD, то C=D.
Доказательство. Пусть
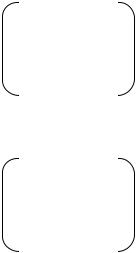
С =
y |
11 |
....y |
1i |
....y |
1n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
......................... |
||||||
|
|
|
|
|
|
|
|
|
|
|
...yni ...ynn |
|
|||
yn1 |
|
||||||
D =
d |
11 |
...d |
1i |
...d |
1n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
........................ |
||||||
|
|
|
|
|
|
|
|
|
|
|
...dni ...dnn |
|
|||
dn1 |
|
||||||
Тогда из равенства eC=eD получаем:
e1y1i+…+enyni= e1d1i+…+endni =b (1) (суммы, стоящие слева, мы обозначили через b). Тогда (1) – два выражения вектора b из L через базис е. Ввиду единственности координат вектора b в базисе е, из (1)
получаем:
y1i=d1i, …, yni=dni для любого i. Следовательно, C=D. Лемма доказана.
Теорема 2. Пусть L – n-мерное линейное пространство над полем Р, линейное преобразование L, e и e` два базиса L. Если A и B – матрицы линейного преобразования , соответственно, в базисах e и e`, то В=Т-1АТ, где Т матрица перехода от базиса е к базису е`.
Доказательство. Так как А и В – матрицы линейного преобразования в базисах e и e`, то (е)=еА,
(2)
(е`)=e`B. |
(3) |
Обозначим через Т матрицу перехода от |
e к e`, т.е. справедливо равенство e`=eT. |
(4) |
|
Подставим e` из (4) в (3): (eT)=(eT)B=e(TB) . |
(5) |
Докажем, что (eT)= (e)T . |
(6) |
i-й элемент матрицы (еТ) равен
n( e j ji ) j 1
n (e j )
j 1
ji
, так как – линейное преобразование.
Справа мы получили i-й элемент матрицы (е)Т. Этим доказано равенство (6).
В силу (6) (еТ)= (е)Т=(еА)Т=е(АТ) . |
(7) |
Подставляя (7) в левую часть (5), получаем: е(АТ)=е(ТВ). Отсюда, в силу леммы 3, АТ=ТВ. Так как
матрица Т невырожденная, то для нее существует обратная матрица Т-1. Из последнего равенства имеем: В=Т-1АТ.
Теорема доказана.
Определение 4. Две матрицы С и D, связанные равенством
С= Q-1DQ (для некоторой невырожденной матрицы Q) называются подобными; говорят также, что С получается из D путем трансформирования матрицей Q (все матрицы – над одним полем Р).
Справедливо утверждение, обратное теореме 2.
Теорема 3. Любые две подобные матрицы А и В n-го порядка над полем Р задают одно и то же линейное преобразование произвольного n-мерного линейного пространства над Р.
Доказательство. По условию В= Q-1АQ, где |Q| 0. Рассмотрим произвольное n-мерное линейное пространство L над Р. Пусть е некоторый базис L. В силу следствия теоремы 1, существует линейное преобразование этого пространства, которое в базисе е имеет заданную матрицу А. Так как |Q| 0, то e`=eQ является базисом L, и Q матрица перехода от е к е`. По теореме 2 преобразование в базисе е` имеет матрицу Q-1AQ, а она по условию равна В.
Теорема доказана.
Понятие о нормальной форме Жордана
В силу теоремы 2 матрицы линейного преобразования конечномерного линейного пространства над полем Р в разных базисах подобны. Естественно возникает вопрос: нельзя ли среди всех подобных матриц выбрать «наиболее простую»? Этот вопрос решается положительно для поля С комплексных чисел.
Определение 5. Матрица вида
|
01 |
0 |
|
J0= |
. |
называется клеткой Жордана |
|
. |
|||
|
( 0 некоторый элемент поля Р). |
||
|
. |
1 |
|
|
0 |
0 |
|
Определение 6. Матрица вида |
|||
|
J1 |
0 |
|
J= |
. |
|
|
. |
|
||
|
|
||
|
. |
|
|
|
0 |
Js |
|
,
по главной диагонали которой стоят клетки Жордана, называется матрицей Жордана.
Справедлива следующая Теорема 4. Всякая матрица А с комплексными элементами подобна некоторой матрице Жордана с
комплексными элементами (последняя называется нормальной формой Жордана матрицы А). Доказательство этой и более общей теорем (для произвольного поля) требует изложения обширного
материала и выходит за рамки данного пособия. Его можно найти, например, в [1].
§4. Операции над линейными преобразованиями
Определим во множестве Ф всех линейных преобразований линейного пространства L над полем Р ряд естественных операций. Пусть , Ф.
Определение 7. Суммой линейных преобразований и называют преобразование, + задаваемое так: (+ )(а)= (а)+ (а) (для любого аL).
Утверждение 1. Сумма линейных преобразований линейного пространства L также является также линейным преобразованием L.
Доказательство. Для любых a, b L по определению 1 имеем:
(+ )(а+b)= (a+b)+ (a+b)= (a)+ (b)+ (a)+ (b)=(+)(a)+(+)(b) (при доказательстве мы использовали линейность и ).
Аналогично для любого вектора аL и числа P имеем:
(+)( a)= ( a)+ ( a)= (a)+ (a)= ( (a)+ (a))= [(+)(a)].
Мы проверили свойства линейности для + . Значит ( +) Ф. Утверждение доказано.
Утверждение 2. Матрицей суммы линейных преобразований конечномерного линейного пространства в фиксированном базисе является сумма матриц слагаемых в том же базисе.
Доказательство. Пусть и в базисе е линейного пространства L имеют матрицы А и В. Тогда для любого вектора а из L имеем: [(a)]=A[a], [ (a)]=B[a]. Так как ( + )(а)= (а)+ (а), то
[(+)(a)]=[ (a)]+[ (a)]=А[а]+В[а]=(A+B)[а]. Из равенства [( +)(a)]=(A+B)[a] в силу замечания 4 к
утверждению 1 из §2 данной главы, следует, что ( + ) имеет в базисе е матрицу A+B. Утверждение доказано.
Утверждение 3. Операция сложения линейных преобразований в Ф ассоциативна и коммутативна.
Доказательство. Докажем ассоциативность. Пусть , и Ф. Тогда, для любого а из L имеем:
[(+) + ](а) = ( + )(а)+ (а)= (а)+ (а)+ (а) = (а)+( + )(а) = [+(+ )](а), т.е. справедливо равенство:
[(+)+]а=[+(+ )]а. Это означает равенство линейных преобразований (+) + и +(+ ) (по определению равенства отображений). Ассоциативность доказана.
Осталось доказать коммутативность. Для любых и из Ф выполняются равенства ( + )(а)= (а)+ (а) =(а)+(a)=(+)(a), откуда следует равенство +=+.
Коммутативность доказана. Утверждение доказано.
Замечание 1. Очевидным является существование во множестве Ф нулевого элемента ((а)=0, аL), а также у каждого элемента – противоположному ему.
Утверждение 4. Множество Ф всех линейных преобразований линейного пространства L – это коммутативная группа по сложению.
Справедливость этого вытекает из доказанных выше утверждений 1–3 и замечания 1 к утверждению 3.
Определение 8. Произведением линейного преобразования на число Р называют отображение,
определяемое так: ( )(а)=((а)) для любого аL.
Утверждение 5. Произведение линейного преобразования на число является линейным преобразованием.
Доказательство. Это вытекает из соотношений, выполняющихся при любых a, b L, P: ( )(a+b)= ( (a+b))= ( (a)+ (b))=( )(a)+( )(b),
( )( a)= [ ( a)]= ( (a))=( )( (a))= (( )(a)).
Утверждение доказано.
Утверждение 6. При умножении линейного преобразования конечномерного линейного пространства на число его матрица умножается на это число.
Справедливость этого утверждения следует из равенств:
[ (a)]= [ (a)]= (A[a])= ( A)[a] и замечания 4 к утверждению 1 из §2 этой главы.
Из утверждений 4 и 5 нетрудно получить, что Ф – линейное пространство над полем Р.
Определение 9. Произведением линейных преобразований и из Ф называют результат их последовательного применения, т.е. преобразование , действующее по правилу: ( )(а)=((а)) для любого аL (преобразование, действующее первым, записывают справа).
Замечание 2. В определении 9 использована левая запись преобразований. Иногда используют правую запись: a( )=(a ) . Тогда произведение и обозначают через .
Утверждение 7. Преобразование является линейным, т.е. принадлежит Ф.
Справедливость этого утверждения вытекает из следующих соотношений (для любых a, b из L и любого
P):
( )(a+b)= ( (a+b))= ( a+ b)=( )(a)+( )(b), ( )( a)= ( ( a))= ( (a))= ( (a))= ( (a)).
Значит, Ф, т.е. умножение преобразований является алгебраической операцией в Ф. Утверждение доказано.
Утверждение 8. Пусть в конечномерном линейном пространстве L выбран базис е. Если А и В – матрицы преобразований , Ф в базисе e, то матрицей в базисе e является матрица BA (матрица преобразования, действующего первым, записывается справа).
Доказательство. Из равенства ( )(а)=((а)) вытекает: [(a)]=[ ( (a))]= B[ (a)]=ВА[а]. В силу замечания 4 к утверждению 1 из §2 имеет в базисе е матрицу ВА.
Утверждение доказано.
Замечание 3. При доказательстве утверждений о матрицах линейных преобразований +, , мы использовали метод, предложенный Г.С. Шевцовым в [5].
§ 5. Ядро и область значений линейного преобразования
Определение 10. Пусть – линейное преобразование линейного пространства L. Множество (L) образов всех векторов из L при действии называют областью значений преобразования (т.е. (L)={ (a)| a L}).
Утверждение 1. Область значений (L) линейного преобразования является подпространством L. Доказательство. Действительно, если b1, b2(L), то b1= (a1), b2= (a2), где a1, a2L. Поэтому
b1+b2= (a1)+ (a2)= (a1+a2)(L). Аналогично b1= (a1)= ( a1)(L). Следовательно, множество (L)
является подпространством линейного пространства L. Утверждение доказано.
Определение 11. Пусть L конечномерное линейное пространство. Размерность области значений (L) линейного преобразования пространства L называют рангом линейного преобразования .
Теорема 5. Ранг линейного преобразования равен рангу матрицы этого преобразования (в любом базисе).
(
Доказательство. Пусть е=(е1,…,en) |
– |
базис |
L. Для любого аL имеем: |
a |
||||
a) |
n |
(e ) . Это означает, что (L)=< (e |
), (e |
),…,(e |
)>. Тогда dim (L) равна рангу |
|||
|
||||||||
|
i |
i |
1 |
2 |
|
n |
|
|
|
i 1 |
|
|
|
|
|
|
|
n
iei . Отсюда i 1
системы векторов
(e1), (e2),…,(en) (1). Пусть А матрица преобразования в базисе е. Тогда столбцы А – это координатные столбцы векторов (1) в базисе е. Поэтому ранг системы (1) равен рангу rA матрицы А, т.е. dim (L)=rA.
Теорема доказана.
Определение 12. Множество всех векторов линейного пространства L, которые переводятся линейным преобразованием в нулевой вектор, называется ядром линейного преобразования и обозначается Ker .
Легко проверяется, что ядро линейного преобразования является подпространством линейного пространства L.
Определение 13. Если L – конечномерное линейное пространство, то размерность ядра линейного преобразования этого пространства называют дефектом линейного преобразования .
Примеры.
Рассмотрим некоторые линейные преобразования плоскости R2.
1. – проектирование R2 на ось OX. Тогда (L) – это все векторы оси OX, Ker – все векторы оси OY. Ранг и дефект равны 1.
2.– поворот плоскости на угол k. Тогда (R2)=R2, Ker=0. Ранг равен 2, дефект равен 0.
3.– симметрия плоскости относительно начала координат. Тогда (R2)=R2, Ker=0. Ранг равен 2, дефект равен 0.
Теорема 6. Пусть L – n-мерное линейное пространство над полем Р, – его линейное преобразование. Если ранг равен r, то дефект равен n-r (т.е. dim Ker =n-r).
Доказательство. Вектор b L содержится в Ker тогда и только тогда, когда (b)=0 (2). Если е – некоторый базис L, А – матрица в этом базисе, то (2) выполняется тогда и только тогда, когда А[b]=0, т.е. [b] – решение однородной системы АХ=0 (3). Так как по теореме 5 ранг А равен r, то пространство решений этой системы имеет размерность (n-r). Но это пространство решений изоморфно Ker , так как координатные столбцы всех векторов из Ker , и только таких векторов, удовлетворяют системе (3). Значит, dim Ker =n-r.
Теорема доказана.
Следствие. Если L – n-мерное линейное пространство, то dim (L)+dim Ker =n.
Справедливость этого утверждения вытекает из теорем 5 и 6, ибо r+(n-r)=n.
Невырожденные линейные преобразования
Определение 14. Линейное преобразование конечномерного линейного пространства L называется невырожденным, если оно удовлетворяет любому из следующих условий, равносильность которых нетрудно вытекает из доказанных выше теорем:
1.Ранг преобразования равен n;
2.Областью значений служит все пространство L (т.е. (L)=L);
3.Дефект преобразования равен нулю.
Для невырожденных линейных преобразований можно указать и ряд других равносильных условий, в частности, приводимые ниже 4-6.
4. Различные векторы пространства L имеют при преобразовании различные образы.
Действительно, если преобразование обладает свойством 4, то ядро этого преобразования состоит лишь из нулевого вектора , т.е. выполняется свойство 3. Если же векторы а и b таковы, что a≠b, но (а)= (b), то a- b≠0, но (a-b)=0, т.е. свойство 3 не выполняется.
Из 2 и 4 вытекает
5. Преобразование является взаимно однозначным отображением L на себя.
Из 5 следует, что для невырожденного линейного преобразования существует обратное преобразование-1, переводящее всякий вектор (а) в вектор а: -1( (а))=а.
Преобразование -1 будет линейным, так как -1( (а)+ (b))=
-1[ (a+b)]=(a+b), -1[ ( (a))]= -1[ ( a)]= a.
Из определения преобразования -1 вытекает, что -1= (4), где тождественное преобразование. Равенство (4) можно рассматривать, как определение обратного преобразования. Отсюда и из доказанного выше следует, что если невырожденное линейное преобразование задается в некотором базисе матрицей А, невырожденной ввиду свойства 1, то преобразование -1 задается в этом же базисе матрицей А-1. Поэтому из 5 вытекает
6. Для линейного преобразования существует обратное линейное преобразование -1. Так как из 6 следует 1, то все условия 1-6 равносильны.
§ 6. Собственные значения и собственные векторы линейного преобразования
Пусть А – квадратная матрица n-го порядка, А=(aij).
Определение 15. Матрицу
a11- ……a1n
……………
А- Е= an1……ann-
,
где числа aij элементы поля Р и – переменная, называют характеристической матрицей матрицы А. Ее определитель
( )=|A- E| представляет собой многочлен от переменной степени n. Этот многочлен называют
характеристическим многочленом матрицы А.
Характеристический многочлен матрицы А порядка n имеет вид:
( )= р0 n+p1 n-1+…+pn.
Нетрудно проверить, что p0=(-1)n, p1=(-1)n-1(a11+a22+…+ann),…, pn=|A| (ибо pn = (0)).
Определение 16. Корни характеристического многочлена |A- E| называют характеристическими корнями матрицы А.
Заметим, что характеристические корни матрицы А могут и не принадлежать полю Р, но всегда существуют в некотором расширении поля Р (и все они находятся в поле разложения многочлена ( )).
Определение 17. Множество всех характеристических корней матрицы A, в котором каждый корень повторяется столько раз, какова его кратность, называют спектром матрицы А.
В соответствии с формулами Виета коэффициенты характеристического многочлена связаны с его корнями 1, 2, .., n следующим образом:
p1=1+…+ n, p2=1 2+ 1 3+…+ n-1 n,
…………,
pn=1 2… n.
Из этих формул, и отмеченного выше вида коэффициентов p1,…, pn в частности, вытекают часто применяемые соотношения:
1+…+ n=a11+a22+…+ann, 1 2… n=|A|.
Согласно последнему равенству характеристический многочлен матрицы имеет нулевой характеристический корень тогда и только тогда, когда определитель матрицы равен нулю, т.е. эта матрица вырожденная.
Лемма. Характеристические многочлены подобных матриц одинаковы.
Доказательство. Пусть A=Q-1BQ. Тогда, учитывая, что матрица E перестановочна с любой матрицей и
|Q-1|=|Q|-1, имеем:
|A-E|=|Q-1BQ-E|=|Q-1BQ-Q-1Q E|=|Q-1BQ-Q-1EQ|=|Q-1(B-E)Q|= |Q|-1|B-E||Q|=|B-E|.
Лемма доказана.
Так как матрица линейного преобразования в разных базисах подобны, то из леммы вытекает Следствие. Матрицы линейного преобразования в разных базисах конечномерного линейного
пространства имеют один и тот же набор характеристических корней.
Поэтому эти корни можно назвать характеристическими корнями преобразования .
Определение 18. Спектр матрицы линейного преобразования в любом базисе называется спектром линейного преобразования .
С понятием характеристического корня линейного преобразования тесно связано приводимое ниже понятие собственного значения .
Определение 19. Пусть – линейное преобразование линейного пространства L над полем Р. Ненулевой
вектор a L называют собственным вектором преобразования , если этим преобразованием он переводится в вектор 0a, т.е. (a)=0a, где 0 – некоторое число из поля Р, называемое собственным
значением преобразования . При этом говорят, что собственный вектор a принадлежит собственному значению 0 (или относится к этому собственному значению).
Заметим, что нулевой вектор не считается собственным вектором никакого линейного преобразования.
Примеры:
1.Пусть L – любое линейное пространство, – его линейное преобразование, задаваемое так: (а)= 0а a L (преобразование растяжения). Тогда собственными векторами будут все ненулевые векторы из L, а
собственные значения только число 0.
Следующие два примера – для пространства R2 векторов-отрезков на плоскости.
2.– проектирование R2 на ось ОХ. Тогда собственными векторами будут все ненулевые векторы оси ОХ (так как, если аOX\О, то (a)=a=1 a), и все ненулевые векторы оси OY (если b OY\O, то (b)=0=0 b).
Собственные значения – числа 1 и 0.
3. – поворот плоскости на угол k. Так как при таком повороте ни один вектор, отличный от нуля, не остается на своей прямой (т.е. не переходит в пропорциональный), то не имеет собственных векторов.
Теорема 7. Собственными значениями линейного преобразования , действующего в конечномерном линейном пространстве L над полем Р, являются характеристические корни этого преобразования, принадлежащие полю Р, и только они.
Доказательство. 1. Пусть линейное преобразование в некотором базисе е имеет матрицу А и число 0
является собственным значением линейного преобразования . Тогда 0 Р и существует аL\0, что справедливо равенство (a)=0a (1). Если –тождественное преобразование, то 0а=(0а)=( 0 )(а). Так как в
силу (1) (а)- 0a=0,
то мы получаем: (а)- 0a=(а)-(0 )(а)=( - 0 )(а)=0 (2).
Пусть А – матрица в базисе е. Тогда равенство (1) равносильно координатному равенству (А- 0Е)[a]=0 (3), где [a] – столбец координат вектора а в базисе е.
Матричное равенство (3) показывает, что столбец [a] является решением однородной системы линейных уравнений (А- 0Е)Х=0 (4). Так как вектор а ненулевой, то система (4) имеет ненулевые решения, и потому ее определитель равен нулю, т.е. |A- 0E|=0 (5). Значит, число 0 является характеристическим корнем преобразования , содержащимся в Р.
2. Докажем обратное утверждение.
Пусть 0 – характеристический корень , принадлежащий Р. Тогда выполняется (5), т.е. определитель однородной системы (4) равен нулю, и эта система имеет ненулевое решение, т.е. для некоторого вектора a0 выполняется (3). А тогда вектор а удовлетворяет условиям (2) и (1). Поэтому, по определению, а – собственный вектор преобразования . Так как 0 Р, то из (1) следует, что 0 – собственное значение .
Теорема доказана.
Замечание 1. Если ввести обозначения:
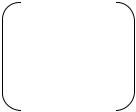
СЗ – множество собственных значений , ХК – множество характеристических корней , то теорема 7 примет вид: ХК Р=СЗ .
Так как все корни многочлена с комплексными коэффициентами комплексные, то из теоремы 7 получаем Следствие. В конечномерном комплексном линейном пространстве собственными значениями любого его линейного преобразования являются все его характеристические корни, и только они. В конечномерном действительном линейном пространстве собственными значениями линейного преобразования являются
все его действительные характеристические корни, и только они.
Замечание 2. Из этого следствия вытекает следующее правило. Для отыскания всех собственных значений линейного преобразования с матрицей А нужно найти все характеристические корни матрицы А и из них выбрать лишь те, которые принадлежат основному полю Р. Для отыскания всех собственных векторов линейного преобразования с матрицей А нужно для каждого собственного значения 0 найти все ненулевые решения системы (4).
§ 7. Линейные преобразования с простым спектром
Во многих случаях оказывается необходимым знать, может ли данное линейное преобразование иметь в некотором базисе диагональную матрицу. На самом деле далеко не всякое линейное преобразование может быть задано диагональной матрицей.
Теорема 8. Линейное преобразование тогда и только тогда задается в базисе е1,…, en диагональной матрицей, если все векторы этого базиса являются собственными векторами преобразования .
Необходимость. Если задается в базисе е диагональной матрицей
1 0
. |
|
(1) |
|
. |
|
|
|
.
0 n ,
то (ei)= iei (2), т.е. ei собственные векторы преобразования (ei≠0, так как содержатся в базисе). Достаточность. Если базис е состоит из собственных векторов преобразования , то справедливы
равенства (2), а тогда имеет в базисе е диагональную матрицу (1). Теорема доказана.
Теорема 9. Собственные векторы b1, ...,bk линейного преобразования , относящиеся к различным собственным значениям, составляют линейно независимую систему.
Доказательство. Будем доказывать это утверждение индукцией по k.. При k=1 оно справедливо – один собственный вектор, будучи отличным от нуля, составляет линейно независимую систему. Пусть (bi)= ibi
(i=1,…,n) и i≠ j при i≠j.
Предположим,что утверждение теоремы 9 верно для (k-1), т.е. b1,…,bk-1 линейно независимая система векторов.
Докажем, что теорема верна и для системы векторов b1,…,bk, удовлетворяющей условию теоремы 6. Если система векторов b1,…,bk линейно зависима, то справедливо равенство 1b1+ 2b2+…+ kbk=0 (3),
где, например, 1≠0. Применяя к обеим частям равенства (3) преобразование , получим:1 1b1+ 2 2b2+…+ k kbk=0. Вычитая отсюда равенство (3), умноженное на k, получим:1( 1- k)b1+…+ k-1( k-1- k)bk-1=0, что дает нетривиальную линейную зависимость между векторами
b1,b2,…,bk-1 так как 1( 1- k)≠0 (ввиду 1≠ k) вопреки предположению индукции. Значит, система b1,…,bk линейно независима.
Теорема доказана.
Определение 20. Говорят, что линейное преобразование линейного пространства L над полем P имеет простой спектр, если все его характеристические корни различны и принадлежат P.
Преобразование с простым спектром имеет, следовательно, п различных собственных значений, а поэтому, по теореме 9, в пространстве L существует базис, составленный из собственных векторов этого преобразования. По теореме 8 в этом базисе имеет диагональную матрицу. Таким образом, справедлива
Теорема 10. Всякое линейное преобразование с простым спект ром конечномерного линейного пространства над полем P в некотором базисе этого пространства имеет диагональную матрицу.
Переходя от линейного преобразования к матрицам, его задающим, мы получаем следующий результат:
Теорема 11. Всякая матрица над полем P, все характеристические корни которой различны и принадлежат P, подобна диагональной матрице или, как говорят, такая матрица приводится к диагональному виду.
