|
41.Интерференция
на тонких пленках, пластинках.
Наблюдаемое в природе радужное
окрашивание тонких пленок (масляные
пленки на воде, мыльные пузыри, оксидные
пленки на металлах) объясняется
интерференцией света, возникающей в
результате отражения света от передней
и задней поверхностей пленки. На
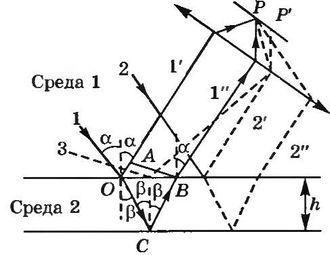
рисунке 17.9 изображена тонкая
плоскопараллельная прозрачная пленка,
на которую падают лучи света. В точке
О свет частично отразится от верхней
поверхности пленки (волна 1′),
а частично преломится и отразится от
задней ее поверхности в точке С и,
преломившись в точке В, выйдет в воздух
параллельно волне 1′.
Волны 1′
и 1′′
когерентны.
 Если
на пути этих лучей поставить собирающую
линзу, то они будут накладываться в
ее фокальной плоскости и давать
интерференционную картину, которая
определяется их оптической разностью
хода Δ=n2(OC+CB)−n1⋅OA±λ2
где член λ2
— обусловлен потерей полуволны при
отражении света от границы раздела
оптически более плотной среды. Если
n2>n1,
то потеря полуволны произойдет в точке
О, и этот член будет со знаком "плюс"
Если
на пути этих лучей поставить собирающую
линзу, то они будут накладываться в
ее фокальной плоскости и давать
интерференционную картину, которая
определяется их оптической разностью
хода Δ=n2(OC+CB)−n1⋅OA±λ2
где член λ2
— обусловлен потерей полуволны при
отражении света от границы раздела
оптически более плотной среды. Если
n2>n1,
то потеря полуволны произойдет в точке
О, и этот член будет со знаком "плюс"
Δ=n2(OC+CB)−n1(OA−λ2).
Если
n2<n1,
то потеря полуволны произойдет в точке
С, и он будет иметь знак "минус"
Δ=n2(OC+CB−λ2)−n1OA.
Пусть
тонкая пленка находится в воздухе (n1
= 1). Из рисунка 17.9 видим, что OA=OBsinα;
OB=2htgβ;
OC=CB=hcosβ,
где α
и β
— углы падения и преломления
соответственно. Тогда физическая
разность хода Δ=2hn2cosβ−2htgβsinα+λ2.
Из закона преломления найдем, что
sinβ=sinαn2.
Учтем, что cosβ=1−sin2β−−−−−−−−√,
а tgβ=sinβ1−sin2β√.
После несложных математических
преобразований получим:
Δ=2hn2cosβ+λ2
или Δ=2hn22−sin2α−−−−−−−−−√+λ2
1.
Полосы равного наклона.
Как видно из последней формулы,
интерференционная картина определяется
значениями длины волны λ,
толщины пластинки h,
показателя преломления n
и угла падения α.
Для данных λ,
n
и h
каждому наклону соответствует своя
интерференционная полоса. Интерференционные
полосы, возникающие в результате
наложения лучей, падающих на
плоскопараллельную пленку под
одинаковыми углами, называются полосами
равного наклона.
Лучи 3, наклоненные под другим углом,
соберутся в другой точке P′.
Если оптическая ось линзы перпендикулярна
поверхности пластинки, полосы равного
наклона будут иметь вид концентрических
колец с центром в фокусе линзы. 2.
Полосы равной толщины.
На рисунке 17.10 изображена клиновидная
пластинка (угол α
между боковыми гранями мал). На нее
падает свет, направление распространения
которого совпадает с параллельными
лучами 1
и 2.
 Когерентные
лучи 1′
и 1′′
дают интерференционную картину в
точке А', которая определяется разностью
хода этих лучей и будет зависеть от
толщины h
клина в месте падения на него луча.
Лучи 2′
и 2′′
собираются линзой в точке А′′.
Оптическая разность хода определяется
толщиной h'
.
Таким образом, на экране наблюдаются
интерференционные полосы. Каждая из
полос возникает за счет отражения от
мест пластинки, имеющих одинаковую
толщину. Интерференционные полосы на
поверхности пленки имеют одинаковую
освещенность на всех точках поверхности,
соответствующих одинаковым толщинам
пленки, и называются полосами
равной толщины.
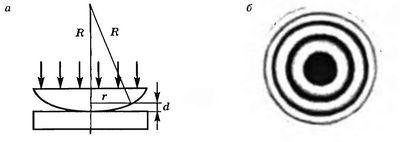
Примером полос равной толщины являются
кольца Ньютона, которые наблюдаются
при отражении света от воздушного
зазора, образованного плоскопараллельной
пластинкой и соприкасающейся с ней
плосковыпуклой линзой с большим
радиусом кривизны (рис. 17.11, а). Воздушная
прослойка постепенно утолщается от
точки соприкосновения линзы к краям.
Отраженные от верхней и нижней границ
воздушной прослойки световые волны
интерферируют между собой. При этом
получается следующая картина: в точке
соприкосновения наблюдается черное
пятно, окруженное рядом концентрических
световых и черных колец убывающей
ширины (рис. 17.11, б).
Когерентные
лучи 1′
и 1′′
дают интерференционную картину в
точке А', которая определяется разностью
хода этих лучей и будет зависеть от
толщины h
клина в месте падения на него луча.
Лучи 2′
и 2′′
собираются линзой в точке А′′.
Оптическая разность хода определяется
толщиной h'
.
Таким образом, на экране наблюдаются
интерференционные полосы. Каждая из
полос возникает за счет отражения от
мест пластинки, имеющих одинаковую
толщину. Интерференционные полосы на
поверхности пленки имеют одинаковую
освещенность на всех точках поверхности,
соответствующих одинаковым толщинам
пленки, и называются полосами
равной толщины.
Примером полос равной толщины являются
кольца Ньютона, которые наблюдаются
при отражении света от воздушного
зазора, образованного плоскопараллельной
пластинкой и соприкасающейся с ней
плосковыпуклой линзой с большим
радиусом кривизны (рис. 17.11, а). Воздушная
прослойка постепенно утолщается от
точки соприкосновения линзы к краям.
Отраженные от верхней и нижней границ
воздушной прослойки световые волны
интерферируют между собой. При этом
получается следующая картина: в точке
соприкосновения наблюдается черное
пятно, окруженное рядом концентрических
световых и черных колец убывающей
ширины (рис. 17.11, б).
 Как
для полос равного наклона, так и для
полос равной толщины, положения
максимумов зависят от λ.
Поэтому при освещении монохроматическим
светом получается система темных и
ярких полос, а при наблюдении в белом
свете интерференционная картина
приобретает радужную окраску.
Интерференцию можно наблюдать и в
проходящем свете, причем в данном
случае не происходит потери полуволны.
В результате максимумы интерференции
в отраженном свете соответствуют
минимумам в проходящем и наоборот. Как
для полос равного наклона, так и для
полос равной толщины, положения
максимумов зависят от λ.
Поэтому при освещении монохроматическим
светом получается система темных и
ярких полос, а при наблюдении в белом
свете интерференционная картина
приобретает радужную окраску.
Интерференцию можно наблюдать и в
проходящем свете, причем в данном
случае не происходит потери полуволны.
В результате максимумы интерференции
в отраженном свете соответствуют
минимумам в проходящем и наоборот.
|
42.Интерферометры
Майкельсона, Фабри-Перо.
Интерферометр Майкельсона Понятие
временной когерентности прямо связано
с интерференционным экспериментом.
Рассмотрим Интерферометр Майкельсона
(Рис.6). Волна падает на наклонную
полупрозрачную пластинку П
интерферометра Майкельсона, формирующую
два пучка. Эти пучки отражаются от
зеркал З1
и
З2.
Затем один из них, пройдя через пластинку
П,
а другой, отразившись от нее, поступают
на экран Q,
где интерферируют. В плоскости экрана
расположен детектор, измеряющий
интенсивность (например, фотодетектор,
величина тока которого пропорциональна
средней интенсивности). Расчеты,
подобные выполненным выше, приводят
к выражению для средней интенсивности
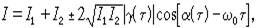 которое сходно с (τ =t2-t1).
Таким образом, изменяя временную
задержку в схеме интерферометра
Майкельсона от τ =0 до τ→∞ , из графика
распределения средней интенсивности
в интерференционной картине
(интерферограмме) можно непосредственно
определить временную корреляционную
функцию светового поля. Как и для
интерферометра Юнга, для интерферометра
Майкельсона можно ввести понятие
видности интерференционной картины.
В данном случае им удобно пользоваться,
если волна квазимонохроматическая,
т.е. Δω/ω0<<1
для такой волны, используя то что
которое сходно с (τ =t2-t1).
Таким образом, изменяя временную
задержку в схеме интерферометра
Майкельсона от τ =0 до τ→∞ , из графика
распределения средней интенсивности
в интерференционной картине
(интерферограмме) можно непосредственно
определить временную корреляционную
функцию светового поля. Как и для
интерферометра Юнга, для интерферометра
Майкельсона можно ввести понятие
видности интерференционной картины.
В данном случае им удобно пользоваться,
если волна квазимонохроматическая,
т.е. Δω/ω0<<1
для такой волны, используя то что
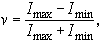 ,
для видности интерференционной картины
в интерферометре Майкельсона вблизи
заданного значения τ при I1=I2
имеем υ=│γ (τ)│ На базе интерферометра
Майкельсона собран интерферометр
Тваймана-Грина. Его отличительной
особенностью является размещение в
измерительном плече оптического
элемента, качество изготовления
которого мы хотим оценить. В случае
призмы второе плечо просто разворачивают,
оставляя в нем плоский отражатель.
Для контроля линз или много линзовых
объективов зеркало М2
делают сферическим. Интерферометр
Фабри-Перо Интерферометр Фабри-Перо
может быть выполнен в виде
плоскопараллельной стеклянной или
кварцевой пластины, на обе поверхности
которых нанесены отражающие слои,
либо в виде двух пластин, у которых
покрытые отражающими слоями плоскости
установлены строго параллельно друг
другу и разделены воздушным промежутком. ,
для видности интерференционной картины
в интерферометре Майкельсона вблизи
заданного значения τ при I1=I2
имеем υ=│γ (τ)│ На базе интерферометра
Майкельсона собран интерферометр
Тваймана-Грина. Его отличительной
особенностью является размещение в
измерительном плече оптического
элемента, качество изготовления
которого мы хотим оценить. В случае
призмы второе плечо просто разворачивают,
оставляя в нем плоский отражатель.
Для контроля линз или много линзовых
объективов зеркало М2
делают сферическим. Интерферометр
Фабри-Перо Интерферометр Фабри-Перо
может быть выполнен в виде
плоскопараллельной стеклянной или
кварцевой пластины, на обе поверхности
которых нанесены отражающие слои,
либо в виде двух пластин, у которых
покрытые отражающими слоями плоскости
установлены строго параллельно друг
другу и разделены воздушным промежутком.
 Рис.
4. Полосы равного наклона при многолучевой
интерференции. Отражение света от
двух параллельных плоскостей приводит
к образованию локализованных в
бесконечности (или фокальной плоскости
линзы) интерференционных полоса
равного наклона. В некоторую точку P
фокальной плоскости линзы собираются
лучи, которые до линзы образуют с ее
оптической осью один и тот же угол Θ
(см.рисунок). Разность хода Δ двух
соседних интерферирующих лучей
определяется формулой: Δ=2nhcosΘ′.
Максимумы интенсивности в проходящем
свете расположатся там, где Δ составляет
целое число длин волн:
Рис.
4. Полосы равного наклона при многолучевой
интерференции. Отражение света от
двух параллельных плоскостей приводит
к образованию локализованных в
бесконечности (или фокальной плоскости
линзы) интерференционных полоса
равного наклона. В некоторую точку P
фокальной плоскости линзы собираются
лучи, которые до линзы образуют с ее
оптической осью один и тот же угол Θ
(см.рисунок). Разность хода Δ двух
соседних интерферирующих лучей
определяется формулой: Δ=2nhcosΘ′.
Максимумы интенсивности в проходящем
свете расположатся там, где Δ составляет
целое число длин волн: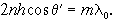 Линиям равных интенсивностей
соответствует одно и то же значение
угла Θ, поэтому интерференционные
полосы в фокальной плоскости линзы
имеют вид концентрических колец с
центром на оси линзы. Центру картины
соответствует наибольший порядок
интерференции. При этом расположение
максимумов интенсивности будет таким
же, как в полоса равного наклона при
двухлучевой интерференции. Однако
для определения структуры максимумов
в случае высокого коэффициента
отражения светоделительных поверхностей
необходимо учесть интерференцию всех
приходящих в точку P
волн, образующихся при многократных
отражениях. Важным преимуществом
интерферометра Фабри-Перо
является его большая светосила. Его
угловая дисперсия значительно превышает
дисперсию других аналогичных аппаратов.
Он используется также в объемных
резонаторах оптических квантовых
генераторов (лазеров).
Линиям равных интенсивностей
соответствует одно и то же значение
угла Θ, поэтому интерференционные
полосы в фокальной плоскости линзы
имеют вид концентрических колец с
центром на оси линзы. Центру картины
соответствует наибольший порядок
интерференции. При этом расположение
максимумов интенсивности будет таким
же, как в полоса равного наклона при
двухлучевой интерференции. Однако
для определения структуры максимумов
в случае высокого коэффициента
отражения светоделительных поверхностей
необходимо учесть интерференцию всех
приходящих в точку P
волн, образующихся при многократных
отражениях. Важным преимуществом
интерферометра Фабри-Перо
является его большая светосила. Его
угловая дисперсия значительно превышает
дисперсию других аналогичных аппаратов.
Он используется также в объемных
резонаторах оптических квантовых
генераторов (лазеров).
|
43.Интерференция
на толстых пластинках.
Полосы равного наклона. ПОЛОСЫ РАВНОГО
НАКЛОНА - чередующиеся тёмные и светлые
полосы (интерференционные полосы),
возникающие при падении света на
плоскопараллельную пластину в
результате интерференции лучей,
отражённых от верхней и нижней её
поверхностей и выходящих параллельно
друг другу. Монохроматич. свет
с длиной волны
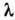 от
точечного источника S
(рис.), находящегося в среде с показателем
преломления п,
падает на пластину толщиной h
и с показателем преломления от
точечного источника S
(рис.), находящегося в среде с показателем
преломления п,
падает на пластину толщиной h
и с показателем преломления
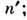 при
отражении луча SA
от верхней и нижней граней образуются
параллельные лучи AD
и СЕ.
Оптич. разность
хода между такими лучами при
отражении луча SA
от верхней и нижней граней образуются
параллельные лучи AD
и СЕ.
Оптич. разность
хода между такими лучами
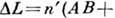 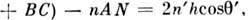 а
соответствующая разность фаз а
соответствующая разность фаз
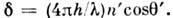 С
учётом сдвига фаз на С
учётом сдвига фаз на
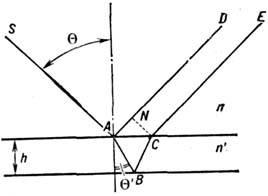
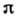 при
отражении при
отражении
 т.
е. при постоянстве h
и т.
е. при постоянстве h
и
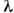 разность
фаз разность
фаз
 определяется
наклоном лучей относительно пластины:
при равном наклоне p разность фаз
постоянна. Чтобы лучи AD
и СЕ
интерферировали, необходимо их
совмещение, что достигается для
параллельных лучей в бесконечности.
Наблюдаются они при аккомодации глаз
на бесконечность или с помощью линзы,
в фокусе к-рой помещают экран. Разность
фаз определяется
наклоном лучей относительно пластины:
при равном наклоне p разность фаз
постоянна. Чтобы лучи AD
и СЕ
интерферировали, необходимо их
совмещение, что достигается для
параллельных лучей в бесконечности.
Наблюдаются они при аккомодации глаз
на бесконечность или с помощью линзы,
в фокусе к-рой помещают экран. Разность
фаз
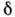 не
связана с положением источника света:
лучи, испущенные соседней точкой
источника и отражённые под тем же
углом не
связана с положением источника света:
лучи, испущенные соседней точкой
источника и отражённые под тем же
углом
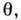 будут
иметь ту же разность фаз, а при
проецировании на экран попадут в ту
же точку. Поэтому при использовании
протяжённого источника полосы
оказываются столь же отчётливыми, как
и с точечным источником. Если оптич.
ось пучка света нормальна к пластинке
( будут
иметь ту же разность фаз, а при
проецировании на экран попадут в ту
же точку. Поэтому при использовании
протяжённого источника полосы
оказываются столь же отчётливыми, как
и с точечным источником. Если оптич.
ось пучка света нормальна к пластинке
(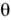 =
0), то П. р. н. приобретают вид концентрич.
колец, что используется в частности
в интерферометре
Фабри- Перо,
полосы на выходе к-рого - пример П. р.
н. Благодаря большому отношению =
0), то П. р. н. приобретают вид концентрич.
колец, что используется в частности
в интерферометре
Фабри- Перо,
полосы на выходе к-рого - пример П. р.
н. Благодаря большому отношению
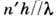 у
интерферометра Фабри - Перо небольшие
изменения у
интерферометра Фабри - Перо небольшие
изменения
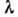 ведут
к большому изменению ведут
к большому изменению
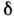 ,
что позволяет использовать интерферометр
Фабри - Перо как спектральный прибор
высокой разрешающей силы либо как
частотный фильтр в открытом
резонаторе. ,
что позволяет использовать интерферометр
Фабри - Перо как спектральный прибор
высокой разрешающей силы либо как
частотный фильтр в открытом
резонаторе.
|
|
44.Дифракция.
Принцип Гюйгенса. Принцип Гюйгенса
Френеля.
Дифракцией
называется огибание волнами препятствий,
встречающихся на их пути, или в более
широком смысле — любое отклонение
распространения волн вблизи препятствий
от законов геометрической оптики.
Благодаря дифракции волны могут
попадать в область геометрической
тени, огибать препятствия, проникать
через небольшие отверстия в экранах
и т. д. Например, звук хорошо слышен за
углом дома, т. е. звуковая волна его
огибает. Явление дифракции объясняется
с помощью принципа
Гюйгенса,
согласно которому каждая точка, до
которой доходит волна, служит центром
вторичных волн, а огибающая этих волн
задает положение волнового фронта в
следующий момент времени. Явление
дифракции характерно для волновых
процессов. Поэтому если свет является
волновым процессом, то для него должна
наблюдаться дифракция, т. е. световая
волна, падающая на границу какого-либо
непрозрачного тела, должна огибать
его (проникать в область геометрической
тени). Из опыта, однако, известно, что
предметы, освещаемые светом, идущим
от точечного источника, дают резкую
тень и, следовательно, лучи не отклоняются
от их прямолинейного распространения.
Почему же возникает резкая тень, если
свет имеет волновую природу? К сожалению,
теория Гюйгенса ответить на этот
вопрос не могла. Принцип Гюйгенса
решает лишь задачу о направлении
распространения волнового фронта, но
не затрагивает вопроса об амплитуде,
а следовательно, и об интенсивности
волн, распространяющихся по разным
направлениям. Френель вложил в принцип
Гюйгенса физический смысл, дополнив
его идеей интерференции вторичных
волн. Согласно
принципу Гюйгенса — Френеля,
световая волна, возбуждаемая каким-либо
источником S,
может быть представлена как результат
суперпозиции когерентных вторичных
волн,
«излучаемых» фиктивными источниками.
Такими источниками могут служить
бесконечно малые элементы любой
замкнутой поверхности, охватывающей
источник S.
Обычно в качестве этой поверхности
выбирают одну из волновых поверхностей,
поэтому все фиктивные источники
действуют синфазно. Таким образом,
волны, распространяющиеся от источника,
являются результатом интерференции
всех когерентных вторичных волн.
Френель исключил возможность
возникновения обратных вторичных
волн и предположил, что если между
источником и точкой наблюдения
находится непрозрачный экран с
отверстием, то на поверхности экрана
амплитуда вторичных волн равна нулю,
а в отверстии — такая же, как при
отсутствии экрана. Учет амплитуд и
фаз вторичных волн позволяет в каждом
конкретном случае найти амплитуду
(интенсивность) результирующей волны
в любой точке пространства, т. е.
определить закономерности распространения
света. В общем случае расчет интерференции
вторичных волн довольно сложный и
громоздкий, однако, как будет показано
ниже, для некоторых случаев нахождение
амплитуды результирующего колебания
осуществляется алгебраическим
суммированием.
|
45.Зоны
Френеля. Зонная пластинка.
Вычисление
интеграла по формуле (2) в общем случае
затруднительно. Френель решил задачу
нахождения амплитуды в т. Р, заменив
интегрирование суммированием, т.е.
перешёл от непрерывных сумм (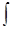 )
к дискретным (Σ). )
к дискретным (Σ).
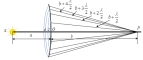 Точечный источник S
создаёт сферическую волну. Требуется
определить амплитуду колебаний волны
в т. Р.
Волновая поверхность в некоторой
точке О
будет
представлять сферу. Френель предложил
разбить ее на кольцевые зоны (секторы)
так, что расстояния от краев каждой
зоны до т. Р
отличается на λ/2. Построенные таким
образом сектора сферы называются
зонами
Френеля.
Волны, приходящие в т. Р
от аналогичных точек двух соседних
зон имеют противоположные фазы, т.к.
разность хода между этими волнами
равна λ/2. При не слишком больших m
(m
–
номер зоны), площади зон Френеля
примерно равны S1=
S2
=Sm.
С ростом номера зоны m
увеличивается расстояние bm,
от зоны до т. Р
и угол φ между нормаль. к элементам
зоны и направлением на т. Р.
Тогда по формуле (1) амплитуда Am
колебания,
возбуждаемогоm
-й-зоной в т. Р,
монотонно убывает А1
>A2
>A3
>Am
>…>A∞.
Т.к. волны от двух соседних зон приходят
в т. Р
в противофазе, они ослабляют друг
друга и тогда результирующая амплитуда
в т. Р
равна Арез
= А1
-A2
+A3
–A4+…
Т.к. Am
монотонно убывает, то можно считать
Точечный источник S
создаёт сферическую волну. Требуется
определить амплитуду колебаний волны
в т. Р.
Волновая поверхность в некоторой
точке О
будет
представлять сферу. Френель предложил
разбить ее на кольцевые зоны (секторы)
так, что расстояния от краев каждой
зоны до т. Р
отличается на λ/2. Построенные таким
образом сектора сферы называются
зонами
Френеля.
Волны, приходящие в т. Р
от аналогичных точек двух соседних
зон имеют противоположные фазы, т.к.
разность хода между этими волнами
равна λ/2. При не слишком больших m
(m
–
номер зоны), площади зон Френеля
примерно равны S1=
S2
=Sm.
С ростом номера зоны m
увеличивается расстояние bm,
от зоны до т. Р
и угол φ между нормаль. к элементам
зоны и направлением на т. Р.
Тогда по формуле (1) амплитуда Am
колебания,
возбуждаемогоm
-й-зоной в т. Р,
монотонно убывает А1
>A2
>A3
>Am
>…>A∞.
Т.к. волны от двух соседних зон приходят
в т. Р
в противофазе, они ослабляют друг
друга и тогда результирующая амплитуда
в т. Р
равна Арез
= А1
-A2
+A3
–A4+…
Т.к. Am
монотонно убывает, то можно считать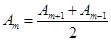 и Арез
можно записать в виде
и Арез
можно записать в виде
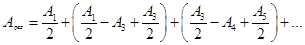
Если
фронт волны полностью открыт, то число
зон m
→ ∞
и
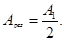 Амплитуда, создаваемая в некоторой
точке Р
всей сферической волновой поверхностью,
равна половине амплитуды первой зоны.
Следовательно, распространение света
от S
к Р
происходит так, будто световой поток
распространяется внутри очень узкого
канала вдоль линии SР.
т. е. прямолинейно. Зонные
пластинки
служат для усиления интенсивности
света в т. Р
путем перекрывания четных (или нечетных)
зон Френеля - амплитудные зонные
пластинки, или изменения фазы волны
на π, при прохождении через более
толстые- четные (нечетные) участки
пластинки - фазовые зонные пластинки.
Амплитуда, создаваемая в некоторой
точке Р
всей сферической волновой поверхностью,
равна половине амплитуды первой зоны.
Следовательно, распространение света
от S
к Р
происходит так, будто световой поток
распространяется внутри очень узкого
канала вдоль линии SР.
т. е. прямолинейно. Зонные
пластинки
служат для усиления интенсивности
света в т. Р
путем перекрывания четных (или нечетных)
зон Френеля - амплитудные зонные
пластинки, или изменения фазы волны
на π, при прохождении через более
толстые- четные (нечетные) участки
пластинки - фазовые зонные пластинки.  Если на- пути световых волн поставить
экран с отверстием, в котором укладывается
четное число зон Френеля, то в т. Р
будет минимум - ослабление света:
Если на- пути световых волн поставить
экран с отверстием, в котором укладывается
четное число зон Френеля, то в т. Р
будет минимум - ослабление света:
 Если в отверстии укладывается нечетное
число зон Френеля, то в т. Р
будет максимум - усиление света
Если в отверстии укладывается нечетное
число зон Френеля, то в т. Р
будет максимум - усиление света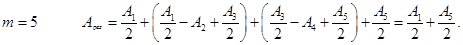 
|
46.Дифракция
от круглого диска.Дифракция
на диске.
Сферическая волна, распространяющаяся
от точечного источника S,
встречает на своем пути диск.
Дифракционную картину наблюдаем на
экране Э в точке В,
лежащей на линии, соединяющей S
с центром диска (рис. 260). В данном случае
закрытый диском участок волнового
фронта надо исключить из рассмотрения
и зоны Френеля строить начиная с краев
диска. Пусть диск закрывает m
первых зон Френеля. Тогда амплитуда
результирующего колебания в точке В
равна
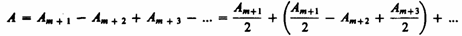 или
или
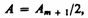 так как выражения, стоящие в скобках,
равны нулю. Следовательно, в точке В
всегда наблюдается
интерференционный максимум (светлое
пятно), соответствующий половине
действия первой открытой зоны Френеля.
Центральный максимум окружен
концентрическими с ним темными и
светлыми кольцами, а интенсивность в
максимумах убывает с расстоянием от
центра картины.
так как выражения, стоящие в скобках,
равны нулю. Следовательно, в точке В
всегда наблюдается
интерференционный максимум (светлое
пятно), соответствующий половине
действия первой открытой зоны Френеля.
Центральный максимум окружен
концентрическими с ним темными и
светлыми кольцами, а интенсивность в
максимумах убывает с расстоянием от
центра картины.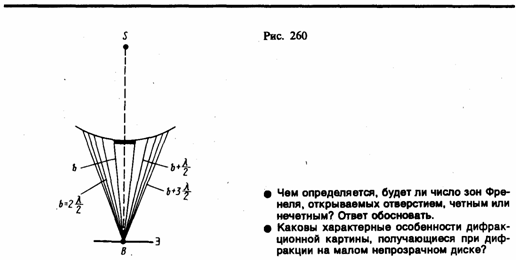 С увеличением радиуса диска первая
открытая зона Френеля удаляется от
точки В
и увеличивается угол т
(см. рис. 258) между нормалью к поверхности
этой зоны и направлением на точку В.
В результате интенсивность центрального
максимума с увеличением размеров
диска уменьшается. При больших размерах
диска за ним наблюдается тень, вблизи
границ которой имеет место весьма
слабая дифракционная картина. В данном
случае дифракцией света можно пренебречь
и считать свет распространяющимся
прямолинейно.Отметим, что дифракция
на круглом отверстии и дифракция на
диске впервые рассмотрены Френелем.
С увеличением радиуса диска первая
открытая зона Френеля удаляется от
точки В
и увеличивается угол т
(см. рис. 258) между нормалью к поверхности
этой зоны и направлением на точку В.
В результате интенсивность центрального
максимума с увеличением размеров
диска уменьшается. При больших размерах
диска за ним наблюдается тень, вблизи
границ которой имеет место весьма
слабая дифракционная картина. В данном
случае дифракцией света можно пренебречь
и считать свет распространяющимся
прямолинейно.Отметим, что дифракция
на круглом отверстии и дифракция на
диске впервые рассмотрены Френелем.
|
|
47.Дифракция
от круглого отверстия. Дифракция
на круглом отверстии.
Сферическая волна, распространяющаяся
из точечного источника S,
встречает на своем пути экран с круглым
отверстием. Дифракционную картину
наблюдаем на экране Э
в точке В,
лежащей на линии, соединяющей S
с центром отверстия (рис. 259). Экран
параллелен плоскости отверстия и
находится от него на расстоянии b.
Разобьем открытую часть волновой
поверхности Ф на зоны Френеля. Вид
дифракционной картины зависит от
числа зон Френеля, открываемых
отверстием. Амплитуда результирующего
колебания, возбуждаемого в точке В
всеми зонами (см. (177.1) и (177.6)),
 где знак плюс соответствует нечетным
m
и минус — четным т.
где знак плюс соответствует нечетным
m
и минус — четным т. Когда отверстие открывает нечетное
число зон Френеля, то амплитуда
(интенсивность) в точке В
будет больше, чем при свободном
распространении волны; если четное,
то амплитуда (интенсивность) будет
равна нулю. Если отверстие открывает
одну зону Френеля, то в точке В
амплитуда А=А1,
т. е. вдвое больше, чем в отсутствие
непрозрачного экрана с отверстием.
Интенсивность света больше соответственно
в четыре раза. Если отверстие открывает
две зоны Френеля, то их действия в
точке В
практически уничтожат друг друга
из-за интерференции. Таким образом,
дифракционная картина от круглого
отверстия вблизи точки В
будет иметь вид чередующихся темных
и светлых колец с центрами в точке В
(если т
четное, то в центре будет темное кольцо,
если m
нечетное — то светлое кольцо), причем
интенсивность в максимумах убывает
с расстоянием от центра картины. Расчет
амплитуды результирующего колебания
на внеосевых участках экрана более
сложен, так как соответствующие им
зоны Френеля частично перекрываются
непрозрачным экраном. Если отверстие
освещается не монохроматическим, а
белым светом, то кольца окрашены. Число
зон Френеля, открываемых отверстием,
зависит от его диаметра. Если он
большой, то
Аm<<A1
и результирующая амплитуда A=A1/2,
т. е. такая же,
как и при
полностью открытом волнов
Когда отверстие открывает нечетное
число зон Френеля, то амплитуда
(интенсивность) в точке В
будет больше, чем при свободном
распространении волны; если четное,
то амплитуда (интенсивность) будет
равна нулю. Если отверстие открывает
одну зону Френеля, то в точке В
амплитуда А=А1,
т. е. вдвое больше, чем в отсутствие
непрозрачного экрана с отверстием.
Интенсивность света больше соответственно
в четыре раза. Если отверстие открывает
две зоны Френеля, то их действия в
точке В
практически уничтожат друг друга
из-за интерференции. Таким образом,
дифракционная картина от круглого
отверстия вблизи точки В
будет иметь вид чередующихся темных
и светлых колец с центрами в точке В
(если т
четное, то в центре будет темное кольцо,
если m
нечетное — то светлое кольцо), причем
интенсивность в максимумах убывает
с расстоянием от центра картины. Расчет
амплитуды результирующего колебания
на внеосевых участках экрана более
сложен, так как соответствующие им
зоны Френеля частично перекрываются
непрозрачным экраном. Если отверстие
освещается не монохроматическим, а
белым светом, то кольца окрашены. Число
зон Френеля, открываемых отверстием,
зависит от его диаметра. Если он
большой, то
Аm<<A1
и результирующая амплитуда A=A1/2,
т. е. такая же,
как и при
полностью открытом волнов
|
48.Дифракция
Фраунгофера на щели
Дифракция
Фраунгофера, имеющая
большое практическое значение,
наблюдается в том случае, когда источник
света и точка наблюдения бесконечно
удалены от препятствия, вызвавшего
дифракцию. Чтобы этот тип дифракции
осуществить, достаточно точечный
источник света поместить в фокусе
собирающей линзы, а дифракционную
картину исследовать в фокальной
плоскости второй собирающей линзы,
установленной за препятствием.
Рассмотрим дифракцию Фраунгофера от
бесконечно длинной щели (для этого
практически достаточно, чтобы длина
щели была значительно больше ее
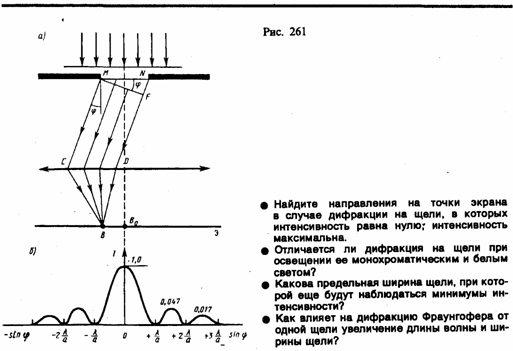
ширины). Пусть плоская монохроматическая
световая волна падает нормально
плоскости узкой щели шириной а
(рис. 261, а).
Оптическая разность хода между крайними
лучами МС
и ND,
идущими от щели в произвольном
направлении ,
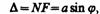 (179.1) где F
— основание
перпендикуляра, опущенного из точки
М
на луч ND.
Разобьем
открытую часть волновой поверхности
в плоскости щели MN
на зоны Френеля, имеющие вид полос,
параллельных ребру М
щели. Ширина каждой зоны выбирается
так, чтобы разность хода от краев этих
зон была равна /2,
т. е. всего на ширине щели уместится
:/2
зон. Так как свет на щель падает
нормально, то плоскость щели совпадает
с волновым фронтом; следовательно,
все точки волнового фронта в плоскости
щели будут колебаться в одинаковой
фазе. Амплитуды вторичных волн в
плоскости щели будут равны, так как
выбранные зоны Френеля имеют одинаковые
площади и одинаково наклонены к
направлению наблюдения. Из выражения
(179.1) вытекает, что число зон Френеля,
укладывающихся на ширине щели, зависит
от угла .
От числа зон Френеля, в свою очередь,
зависит результат наложения всех
вторичных волн. Из приведенного
построения следует, что при интерференции
света от каждой пары соседних
зон Френеля амплитуда результирующих
колебаний равна нулю, так как колебания
от каждой пары соседних зон взаимно
гасят друг друга. Следовательно, если
число зон
Френеля четное,
то
(179.1) где F
— основание
перпендикуляра, опущенного из точки
М
на луч ND.
Разобьем
открытую часть волновой поверхности
в плоскости щели MN
на зоны Френеля, имеющие вид полос,
параллельных ребру М
щели. Ширина каждой зоны выбирается
так, чтобы разность хода от краев этих
зон была равна /2,
т. е. всего на ширине щели уместится
:/2
зон. Так как свет на щель падает
нормально, то плоскость щели совпадает
с волновым фронтом; следовательно,
все точки волнового фронта в плоскости
щели будут колебаться в одинаковой
фазе. Амплитуды вторичных волн в
плоскости щели будут равны, так как
выбранные зоны Френеля имеют одинаковые
площади и одинаково наклонены к
направлению наблюдения. Из выражения
(179.1) вытекает, что число зон Френеля,
укладывающихся на ширине щели, зависит
от угла .
От числа зон Френеля, в свою очередь,
зависит результат наложения всех
вторичных волн. Из приведенного
построения следует, что при интерференции
света от каждой пары соседних
зон Френеля амплитуда результирующих
колебаний равна нулю, так как колебания
от каждой пары соседних зон взаимно
гасят друг друга. Следовательно, если
число зон
Френеля четное,
то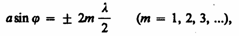 (179.2) и в точке В
наблюдается
дифракционный минимум (полная
темнота), если же число
зон Френеля нечетное,
то
(179.2) и в точке В
наблюдается
дифракционный минимум (полная
темнота), если же число
зон Френеля нечетное,
то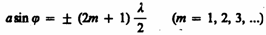 (179.3) и наблюдается дифракционный
максимум,
соответствующий действию одной
нескомпенсированной зоны Френеля.
Отметим, что в направлении =0
щель действует как одна зона Френеля,
и в этом направлении свет распространяется
с наибольшей интенсивностью, т. е. в
точке В0
наблюдается центральный
дифракционный максимум. Из
условий (179.2) и (179.3) можно найти
направления на точки экрана, в которых
амплитуда (а следовательно, и
интенсивность) равна нулю (sinmin
=
m/a)
или максимальна (sinmax
= (2m+1)/(2a)).
Распределение интенсивности на экране,
получаемое вследствие дифракции
(дифракционный спектр),
приведено на рис. 261, б.
Расчеты показывают, что интенсивности
в центральном и последующих максимумах
относятся как 1 : 0,047 : 0,017 : 0,0083 : .... т.е.
основная часть световой энергии
сосредоточена в центральном
максимуме. Из опыта и соответствующих
расчетов следует, что сужение щели
приводит к тому, что центральный
максимум расплывается, а интенсивность
уменьшается (это, естественно, относится
и к другим максимумам). Наоборот, чем
щель шире (а>),
тем картина ярче, но дифракционные
полосы уже, а число самих полос больше.
При а>>
в центре
получается резкое изображение источника
света, т. е. имеет место прямолинейное
распространение света.
(179.3) и наблюдается дифракционный
максимум,
соответствующий действию одной
нескомпенсированной зоны Френеля.
Отметим, что в направлении =0
щель действует как одна зона Френеля,
и в этом направлении свет распространяется
с наибольшей интенсивностью, т. е. в
точке В0
наблюдается центральный
дифракционный максимум. Из
условий (179.2) и (179.3) можно найти
направления на точки экрана, в которых
амплитуда (а следовательно, и
интенсивность) равна нулю (sinmin
=
m/a)
или максимальна (sinmax
= (2m+1)/(2a)).
Распределение интенсивности на экране,
получаемое вследствие дифракции
(дифракционный спектр),
приведено на рис. 261, б.
Расчеты показывают, что интенсивности
в центральном и последующих максимумах
относятся как 1 : 0,047 : 0,017 : 0,0083 : .... т.е.
основная часть световой энергии
сосредоточена в центральном
максимуме. Из опыта и соответствующих
расчетов следует, что сужение щели
приводит к тому, что центральный
максимум расплывается, а интенсивность
уменьшается (это, естественно, относится
и к другим максимумам). Наоборот, чем
щель шире (а>),
тем картина ярче, но дифракционные
полосы уже, а число самих полос больше.
При а>>
в центре
получается резкое изображение источника
света, т. е. имеет место прямолинейное
распространение света.
Положение
дифракционных максимумов зависит от
длины волны ,
поэтому рассмотренная выше дифракционная
картина имеет место лишь для
монохроматического света. При
освещении щели белым светом центральный
максимум наблюдается в виде белой
полоски; он общий для всех длин волн
(при
=0 разность
хода равна нулю для всех ).
Боковые максимумы радужно окрашены,
так как условие максимума при любых
т
различно для разных .
Таким образом, справа и слева от
центрального максимума наблюдаются
максимумы первого (m=1),
второго (т=2)
и других порядков, обращенные
фиолетовым краем к центру дифракционной
картины. Однако они настолько
расплывчаты, что отчетливого разделения
различных длин волн с помощью дифракции
на одной щели получить невозможно.
|
49.Дифракционная
решетка.
Дисперсия и разрешающая сила
дифракционной решетки. Дифракционная
решетка представляет собой совокупность
большого числа N
одинаковых по ширине и параллельных
друг другу щелей, разделенных
непрозрачными промежутками, также
одинаковыми по ширине b
-ширина щели; а
- ширина непрозрачного участка; d
= a + b -период
или постоянная решетки.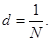 Дифракционная картина на решетке
определяется как результат взаимной
интерференции волн, идущих от всех
щелей, т.е. в дифракционной решетке
осуществляется многолучевая
интерференция. Т.к. щели находятся
друг от друга на одинаковых расстояниях,
то разности хода лучей, идущих от двух
соседних щелей, будут для данного
направления φ одинаковы в пределах
всей дифракционной решетки.
Дифракционная картина на решетке
определяется как результат взаимной
интерференции волн, идущих от всех
щелей, т.е. в дифракционной решетке
осуществляется многолучевая
интерференция. Т.к. щели находятся
друг от друга на одинаковых расстояниях,
то разности хода лучей, идущих от двух
соседних щелей, будут для данного
направления φ одинаковы в пределах
всей дифракционной решетки.
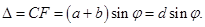 (1) В направлениях, в которых наблюдается
минимум для одной щели, будут минимумы
и в случае N
щелей, т.е. условие главных минимумов
дифракционной решетки будет аналогично
условию минимумов для щели:
(1) В направлениях, в которых наблюдается
минимум для одной щели, будут минимумы
и в случае N
щелей, т.е. условие главных минимумов
дифракционной решетки будет аналогично
условию минимумов для щели: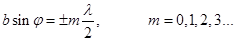 (2) - условие
главных минимумов. Условие
максимумов; те случаи φ, которые
удовлетворяют максимумам для одной
щели, могут быть либо максимумами,
либо минимумами, т.к. всё зависит от
разности хода между лучами. Условие
главных максимумов:
(2) - условие
главных минимумов. Условие
максимумов; те случаи φ, которые
удовлетворяют максимумам для одной
щели, могут быть либо максимумами,
либо минимумами, т.к. всё зависит от
разности хода между лучами. Условие
главных максимумов:
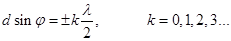 (3) Эти максимумы будут расположены
симметрично относительно центрального
(нулевого k
= 0) максимума.
Для тех углов φ, для которых одновременно
выполняется (2) и (3) максимума не будет,
а будет минимум (например, при d
=2b для всех
четных k
=2р,
р
= 1, 2, 3...). Между главными максимумами
имеются дополнительные очень слабые
максимумы, интенсивность которых во
много раз меньше интенсивности главных
максимумов (1/22 интенсивности ближайшего
главного максимума). Дополнительных
максимумов будет N
- 2, где N
- число штрихов. Условие дополнительных
максимумов:
(3) Эти максимумы будут расположены
симметрично относительно центрального
(нулевого k
= 0) максимума.
Для тех углов φ, для которых одновременно
выполняется (2) и (3) максимума не будет,
а будет минимум (например, при d
=2b для всех
четных k
=2р,
р
= 1, 2, 3...). Между главными максимумами
имеются дополнительные очень слабые
максимумы, интенсивность которых во
много раз меньше интенсивности главных
максимумов (1/22 интенсивности ближайшего
главного максимума). Дополнительных
максимумов будет N
- 2, где N
- число штрихов. Условие дополнительных
максимумов: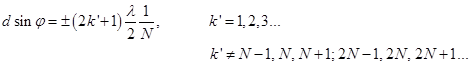 Между
главными максимума будут располагаться
(N-1)
дополнительных минимумов. Условие
дополнительных минимумов: Между
главными максимума будут располагаться
(N-1)
дополнительных минимумов. Условие
дополнительных минимумов: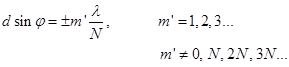 Таким
образом, дифракционная картина, при
дифракции на дифракционной решетке
зависит от N
и от отношения
d/b.
Пусть N
=5,d/b
=4. Тогда число главных максимумов(sin
φ =1) kmax
< d/λ . Между ними по N
-2 = 3 дополнительных максимума и N
– 1 = 4 дополнительных минимума. При
k/m
= d/b
=2,4,8... - главных максимумов не будет, а
будут главные минимумы. Таким образом,
дифракционная картина при дифракции
на дифракционной решетке будет иметь
вид: Таким
образом, дифракционная картина, при
дифракции на дифракционной решетке
зависит от N
и от отношения
d/b.
Пусть N
=5,d/b
=4. Тогда число главных максимумов(sin
φ =1) kmax
< d/λ . Между ними по N
-2 = 3 дополнительных максимума и N
– 1 = 4 дополнительных минимума. При
k/m
= d/b
=2,4,8... - главных максимумов не будет, а
будут главные минимумы. Таким образом,
дифракционная картина при дифракции
на дифракционной решетке будет иметь
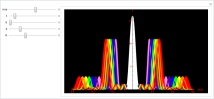
вид: Если решетку освещать монохроматическим
белым светом, то будет картина,
показанная на рис. Если освещать белым
светом, то все максимумы, кроме
центрального (k
= 0) разложатся
в спектр - совокупность составляющих
цветов, причем фиолетовые линии будут
ближе к центру, а красные дальше (т.к.
λф
< λкр
, то φф
< φкр).
Если решетку освещать монохроматическим
белым светом, то будет картина,
показанная на рис. Если освещать белым
светом, то все максимумы, кроме
центрального (k
= 0) разложатся
в спектр - совокупность составляющих
цветов, причем фиолетовые линии будут
ближе к центру, а красные дальше (т.к.
λф
< λкр
, то φф
< φкр).
|
|
50.Дифракция
рентгеновских лучей.
Дифракция
рентгеновских
лучей,
рассеяние рентгеновских лучей
кристаллами (или молекулами жидкостей
и газов), при котором из начального
пучка лучей возникают вторичные
отклонённые пучки той же длины волны,
появившиеся в результате взаимодействия
первичных рентгеновских лучей с
электронами вещества; направление и
интенсивность вторичных пучков зависят
от строения рассеивающего объекта.
Дифрагированные пучки составляют
часть всего рассеянного веществом
рентгеновского излучения. Наряду с
рассеянием без изменения длины волны
наблюдается рассеяние с изменением
длины волны — так называемое
комптоновское рассеяние. Явление Д.
р. л., доказывающее их волновую природу,
впервые было экспериментально
обнаружено на кристаллах немецкими
физиками М. Лауэ,
В. Фридрихом и П. Книппингом в 1912.
Кристалл является естественной
трёхмерной дифракционной
решёткой
для рентгеновских лучей, т.к. расстояние
между рассеивающими центрами (атомами)
в кристалле одного порядка с длиной
волны рентгеновских лучей (~1Å=10-8см).
Д. р. л. на кристаллах можно рассматривать
как избирательное отражение рентгеновских
лучей от систем атомных плоскостей
кристаллической решётки Направление
дифракционных максимумов удовлетворяет
одновременно трём условиям: a
(cos
a
— cos
a0)
= Нl,
b
(cos
b
— cos
b0)
= Kl,
с
(cos
g
— cos
g0)
= Ll.
Здесь а,
b,
с
— периоды кристаллической
решётки
по трём её осям; a0,
b0,
g0
— углы, образуемые падающим, а a, b, g —
рассеянным лучами с осями кристалла;
l — длина волны рентгеновских лучей,
Н,
К,
L
— целые числа. Эти уравнения называются
уравнениями Лауэ. Дифракционную
картину получают либо от неподвижного
кристалла с помощью рентгеновского
излучения со сплошным спектром (так
называемая лауэграмма;
рис. 1),
либо от вращающегося или колеблющегося
кристалла (углы a0,
b0
меняются, а g0
остаётся постоянным), освещаемого
монохроматическим рентгеновским
излучением (l — постоянно), либо от
поликристалла, освещаемого
монохроматическим излучением. В
последнем случае, благодаря тому что
отдельные кристаллы в образце
ориентированы произвольно, меняются
углы a0,
b0,
g0.
Интенсивность дифрагированного луча
зависит в первую очередь от так
называемого структурного фактора,
который определяется атомными
факторами
атомов кристалла, их расположением
внутри элементарной ячейки кристалла,
а также характером тепловых колебаний
атомов. Структурный фактор зависит
от симметрии расположения атомов в
элементарной ячейке. Интенсивность
дифрагированного луча зависит также
от размеров и формы объекта, от
совершенства кристалла и прочего.
Д. р. л. от поликристаллических тел
приводит к возникновению резко
выраженных конусов вторичных лучей.
Осью конуса является первичный луч,
а угол раствора конуса равен 4J (J —
угол между отражающей плоскостью и
падающим лучом). Каждый конус
соответствует определённому семейству
кристаллических плоскостей. В создании
конуса участвуют все кристаллики,
семейство плоскостей которых расположено
под углом J к падающему лучу. Если
кристаллики малы и их приходится очень
большое количество на единицу объёма,
то конус лучей будет сплошным. В случае
текстуры, т. е. наличия предпочтительной
ориентировки кристалликов, дифракционная
картина (рентгенограмма)
будет состоять из неравномерно
зачернённых колец. Метод Д. р. л. на
кристаллах дал возможность определять
длину волны рентгеновских лучей, если
известна структура кристаллической
решётки, благодаря чему возникла
рентгеновская
спектроскопия,
сыгравшая важную роль при установлении
строения атома. Наблюдения Д. р. л.
известной длины волны на кристалле
неизвестной структуры позволяют
установить характер этой структуры
(расположение ионов,
атомов и молекул, составляющих
кристалл), что послужило основой
рентгеновского
структурного анализа.
Д. р. л. наблюдается также при рассеянии
их аморфными твёрдыми телами, жидкостями
и газами. В этом случае на кривой
зависимости интенсивности от угла
рассеяния вокруг центрального пятна
появляются широкие кольца типа гало
(рис. 2).
Положение этих колец (угол J) определяется
средним расстоянием между молекулами
или расстояниями между атомами в
молекуле. Из зависимости интенсивности
от угла рассеяния можно определить
распределение плотности вещества. Д.
р. л. можно наблюдать также на обычной
оптической дифракционной решётке при
скользящем падении (меньше угла полного
отражения) рентгеновских лучей на
решётку. С помощью этого метода можно
непосредственно и с большой точностью
измерять длины волн рентгеновских
лучей.
|
51.Голография.
Гологра́фия
(др.-греч.
ὅλος —
полный + γραφή —
пишу) — набор технологий для точной
записи, воспроизведения и переформирования
волновых
полей,
особый фотографический метод, при
котором с помощью лазера регистрируются,
а затем восстанавливаются изображения
трехмерных объектов, в высшей степени
похожие на реальные. Рассеянные
объектом волны характеризуются
амплитудой и фазой. Регистрация
амплитуды волн не представляет
затруднений; обычная фотографическая
пленка регистрирует амплитуду,
преобразуя ее значения в соответствующее
почернение фотографической эмульсии.
Фазовые соотношения становятся
доступными для регистрации с помощью
интерференции, преобразующей фазовые
соотношения в соответствующие
амплитудные. Интерференция
возникает, когда в некоторой области
пространства складываются несколько
электромагнитных волн, частоты
которых с очень высокой степенью
точности совпадают. Когда записывают
голограмму, в определённой области
пространства складывают две волны:
одна из них идёт непосредственно от
источника (опорная волна), а другая
отражается от объекта записи (объектная
волна). В этой же области размещают
фотопластинку
(или иной регистрирующий материал), в
результате на этой пластинке возникает
сложная картина полос потемнения,
которые соответствуют распределению
электромагнитной энергии (картине
интерференции)
в этой области пространства. Если
теперь эту пластинку осветить волной,
близкой к опорной, то она преобразует
эту волну в волну, близкую к объектной.
Таким образом, мы будем видеть (с той
или иной степенью точности) такой же
свет, какой отражался бы от объекта
записи. Голограмма является записью
интерференционной картины, поэтому
важно, чтобы длины волн (частоты)
объектного и опорного лучей с
максимальной точностью совпадали
друг с другом, и разность их фаз не
менялась в течение всего времени
записи (иначе на пластинке не запишется
чёткой картины интерференции). Поэтому
источники света должны испускать
электромагнитное излучение с очень
стабильной длиной волны в достаточном
для записи временном диапазоне. Крайне
удобным источником света является
лазер.
До изобретения лазеров голография
практически не развивалась (вместо
лазера использовали очень узкие линии
в спектре испускания газоразрядных
ламп,
что очень затрудняет эксперимент). На
сегодняшний день голография предъявляет
одни из самых жёстких требований к
когерентности
лазеров. Чаще всего когерентность
принято характеризовать длиной
когерентности —
той разности оптических путей двух
волн, при которой контраст
интерференционной картины уменьшается
в два раза по сравнению с интерференционной
картиной, которую дают волны, прошедшие
от источника одинаковое расстояние.
Для различных лазеров длина когерентности
может составлять от долей миллиметра
(мощные лазеры, предназначенные для
сварки, резки и других применений,
нетребовательных к этому параметру)
до сотен и более метров (специальные,
так называемые одночастотные лазеры).
|
52.Естественный
и поляризованный свет. Закон Малюса.
Поляризованным называется свет, в
котором направления колебаний светового
вектора упорядочены каким-либо образом.
В естественном свете колебания
различных направлений быстро и
беспорядочно сменяют друг друга.
Следствием теории Максвелла является
поперечность световых волн: векторы
напряженностей электрического Е
и магнитного Н
полей волны взаимно перпендикулярны
и колеблются перпендикулярно вектору
скорости v
распространения волны (перпендикулярно
лучу). Поэтому для описания закономерностей
поляризации света достаточно знать
поведение лишь одного из векторов.
Обычно все рассуждения ведутся
относительно светового
вектора —
вектора напряженности Е
электрического поля (это название
обусловлено тем, что при действии
света на вещество основное значение
имеет электрическая составляющая
поля волны, действующая на электроны
в атомах вещества). Свет представляет
собой суммарное электромагнитное
излучение множества атомов. Атомы же
излучают световые волны независимо
друг от друга, поэтому световая волна,
излучаемая телом в целом, характеризуется
всевозможными равновероятными
колебаниями светового вектора (рис.
272, а;
луч перпендикулярен плоскости рисунка).
В данном случае равномерное распределение
векторов Е
объясняется большим числом атомарных
излучателей, а равенство амплитудных
значений векторов Е
— одинаковой (в среднем) интенсивностью
излучения каждого из атомов. Свет со
всевозможными равновероятными
ориентациями вектора Е
(и, следовательно, Н)
называется естественным.
Свет, в котором направления колебаний
светового вектора каким-то образом
упорядочены, называется поляризованным.
Так, если в результате каких-либо
внешних воздействий появляется
преимущественное (но не исключительное!)
направление колебаний вектора Е
(рис. 272, б),
то имеем
дело с частично
поляризованным светом.
Свет, в котором вектор Е
(и, следовательно, Н)
колеблется только в одном направлении,
перпендикулярном лучу (рис. 272, в),
называется плоско
поляризованным
(линейно
поляризованным).
 Плоскость, проходящая через направление
колебаний светового вектора плоско
поляризованной волны и направление
распространения этой волны, называется
плоскостью
поляризации.
Плоско поляризованный свет является
предельным случаем эллиптически
поляризованного света
— света, для которого вектор Е
(вектор Н)
изменяется со временем так, что его
конец описывает эллипс, лежащий в
плоскости, перпендикулярной лучу.
Если эллипс поляризации вырождается
в прямую (при разности фаз ,
равной нулю или ),
то имеем дело с рассмотренным выше
плоско поляризованным светом, если в
окружность (при
= ±/2
и равенстве амплитуд складываемых
волн), то имеем дело с циркулярно
поляризованным
(поляризованным
по кругу)
светом.
Степенью
поляризации
называется величина
Плоскость, проходящая через направление
колебаний светового вектора плоско
поляризованной волны и направление
распространения этой волны, называется
плоскостью
поляризации.
Плоско поляризованный свет является
предельным случаем эллиптически
поляризованного света
— света, для которого вектор Е
(вектор Н)
изменяется со временем так, что его
конец описывает эллипс, лежащий в
плоскости, перпендикулярной лучу.
Если эллипс поляризации вырождается
в прямую (при разности фаз ,
равной нулю или ),
то имеем дело с рассмотренным выше
плоско поляризованным светом, если в
окружность (при
= ±/2
и равенстве амплитуд складываемых
волн), то имеем дело с циркулярно
поляризованным
(поляризованным
по кругу)
светом.
Степенью
поляризации
называется величина
 где Imax,
и Imin
— соответственно максимальная и
минимальная интенсивности частично
поляризованного света, пропускаемого
анализатором. Для естественного света
Imax=Imin
и
Р=0,
для плоско поляризованного Imin
=0 и Р=1.
Естественный свет можно преобразовать
в плоско поляризованный, используя
так называемые поляризаторы,
пропускающие колебания только
определенного направления (например,
пропускающие колебания, параллельные
главной плоскости поляризатора, и
полностью задерживающие колебания,
перпендикулярные этой плоскости). В
качестве поляризаторов могут быть
использованы среды, анизотропные в
отношении колебаний вектора Е,
например кристаллы (их анизотропия
известна). Из природных кристаллов,
давно используемых в качестве
поляризатора, следует отметить
турмалин.
Рассмотрим классические опыты с
турмалином
(рис. 273). Направим естественный свет
перпендикулярно пластинке турмалина
T1,
вырезанной
параллельно так называемой оптической
оси ОО'.
Вращая кристалл T1
вокруг
направления луча, никаких изменений
интенсивности прошедшего через
турмалин света не наблюдаем. Если на
пути луча поставить вторую пластинку
турмалина T2
и вращать ее вокруг направления луча,
то интенсивность света, прошедшего
через пластинки, меняется в зависимости
от угла к между оптическими осями
кристаллов
по закону
Малюса*:
где Imax,
и Imin
— соответственно максимальная и
минимальная интенсивности частично
поляризованного света, пропускаемого
анализатором. Для естественного света
Imax=Imin
и
Р=0,
для плоско поляризованного Imin
=0 и Р=1.
Естественный свет можно преобразовать
в плоско поляризованный, используя
так называемые поляризаторы,
пропускающие колебания только
определенного направления (например,
пропускающие колебания, параллельные
главной плоскости поляризатора, и
полностью задерживающие колебания,
перпендикулярные этой плоскости). В
качестве поляризаторов могут быть
использованы среды, анизотропные в
отношении колебаний вектора Е,
например кристаллы (их анизотропия
известна). Из природных кристаллов,
давно используемых в качестве
поляризатора, следует отметить
турмалин.
Рассмотрим классические опыты с
турмалином
(рис. 273). Направим естественный свет
перпендикулярно пластинке турмалина
T1,
вырезанной
параллельно так называемой оптической
оси ОО'.
Вращая кристалл T1
вокруг
направления луча, никаких изменений
интенсивности прошедшего через
турмалин света не наблюдаем. Если на
пути луча поставить вторую пластинку
турмалина T2
и вращать ее вокруг направления луча,
то интенсивность света, прошедшего
через пластинки, меняется в зависимости
от угла к между оптическими осями
кристаллов
по закону
Малюса*:
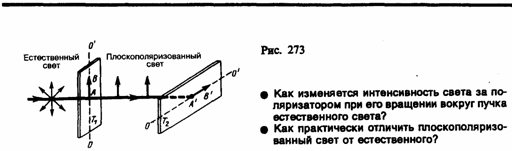
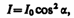 (190.1) где I0
и I
— соответственно интенсивности света,
падающего на второй кристалл и вышедшего
из него. * Э. Малюс (1775—1812) —
французский физик. Следовательно,
интенсивность прошедшего через
пластинки света изменится от минимума
(полное гашение света) при =/2
(оптические оси пластинок перпендикулярны)
да максимума при =0
(оптические оси пластинок параллельны).
Однако, как это следует из рис. 274,
амплитуда Е
световых колебаний, прошедших через
пластинку Т2,
будет меньше амплитуды световых
колебаний Е0,
падающих на пластинку T2.
(190.1) где I0
и I
— соответственно интенсивности света,
падающего на второй кристалл и вышедшего
из него. * Э. Малюс (1775—1812) —
французский физик. Следовательно,
интенсивность прошедшего через
пластинки света изменится от минимума
(полное гашение света) при =/2
(оптические оси пластинок перпендикулярны)
да максимума при =0
(оптические оси пластинок параллельны).
Однако, как это следует из рис. 274,
амплитуда Е
световых колебаний, прошедших через
пластинку Т2,
будет меньше амплитуды световых
колебаний Е0,
падающих на пластинку T2.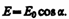 Так
как интенсивность света пропорциональна
квадрату амплитуды, то и получается
выражение (190.1). Результаты опытов с
кристаллами турмалина
объясняются довольно просто, если
исходить из изложенных выше условий
пропускания света поляризатором.
Первая пластинка турмалина пропускает
колебания только определенного
направления (на рис. 273 это направление
показано стрелкой AВ),
т. е. преобразует естественный свет в
плоско поляризованный. Вторая же
пластинка турмалина
в зависимости от ее ориентации из
поляризованного света пропускает
большую или меньшую его часть, которая
соответствует компоненту Е,
параллельному оси второго турмалина.
На рис. 273 обе пластинки расположены
так, что направления пропускаемых ими
колебаний АВ
и А'В' перпендикулярны
друг другу. В данном случае Т1
пропускает колебания, направленные
по АВ,
а Т2
их полностью
гасит, т.е. за вторую пластинку турмалина
свет не проходит. Так
как интенсивность света пропорциональна
квадрату амплитуды, то и получается
выражение (190.1). Результаты опытов с
кристаллами турмалина
объясняются довольно просто, если
исходить из изложенных выше условий
пропускания света поляризатором.
Первая пластинка турмалина пропускает
колебания только определенного
направления (на рис. 273 это направление
показано стрелкой AВ),
т. е. преобразует естественный свет в
плоско поляризованный. Вторая же
пластинка турмалина
в зависимости от ее ориентации из
поляризованного света пропускает
большую или меньшую его часть, которая
соответствует компоненту Е,
параллельному оси второго турмалина.
На рис. 273 обе пластинки расположены
так, что направления пропускаемых ими
колебаний АВ
и А'В' перпендикулярны
друг другу. В данном случае Т1
пропускает колебания, направленные
по АВ,
а Т2
их полностью
гасит, т.е. за вторую пластинку турмалина
свет не проходит.
 Пластинка
Т1,
преобразующая естественный свет в
плоско поляризованный, является
поляризатором.
Пластинка Т2,
служащая для анализа степени поляризации
света, называется анализатором.
Обе пластинки совершенно одинаковы
(их можно поменять местами).Если
пропустить естественный свет через
два поляризатора, главные плоскости
которых образуют угол ,
то из первого выйдет плоско поляризованный
свет, интенсивность которого
I0=1/2Iест,
из второго, согласно (190.1), выйдет свет
интенсивностью I=I0cos2
. Следовательно,
интенсивность света, прошедшего через
два поляризатора, Пластинка
Т1,
преобразующая естественный свет в
плоско поляризованный, является
поляризатором.
Пластинка Т2,
служащая для анализа степени поляризации
света, называется анализатором.
Обе пластинки совершенно одинаковы
(их можно поменять местами).Если
пропустить естественный свет через
два поляризатора, главные плоскости
которых образуют угол ,
то из первого выйдет плоско поляризованный
свет, интенсивность которого
I0=1/2Iест,
из второго, согласно (190.1), выйдет свет
интенсивностью I=I0cos2
. Следовательно,
интенсивность света, прошедшего через
два поляризатора,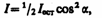 откуда
I0=1/2Iест
(поляризаторы параллельны) и Imin
= 0 (поляризаторы скрещены). откуда
I0=1/2Iест
(поляризаторы параллельны) и Imin
= 0 (поляризаторы скрещены).
|
|
53.Двойное
лучепреломление.
Все прозрачные кристаллы (кроме
кристаллов кубической системы, которые
оптически изотропны) обладают
способностью двойного
лучепреломления,
т. е. раздваивания каждого падающего
на них светового пучка. Это явление,
в 1669 г. впервые обнаруженное датским
ученым Э. Бартолином (1625—1698) для
исландского шпата (разновидность
кальцита СаСОз), объясняется особенностями
распространения света в анизотропных
средах и непосредственно вытекает из
уравнений Максвелла. Если на толстый
кристалл исландского шпата направить
узкий пучок света, то из кристалла
выйдут два пространственно разделенных
луча, параллельных друг другу и
падающему лучу (рис. 277). Даже в том
случае, когда первичный пучок падает
на кристалл нормально, преломленный
пучок разделяется на два, причем один
из них является продолжением первичного,
а второй отклоняется (рис. 278). Второй
из этих лучей получил название
необыкновенного
(e),
а первый — обыкновенного
(о).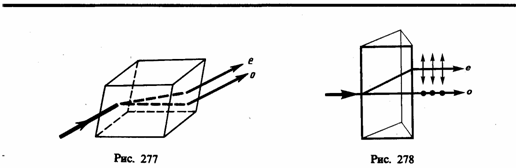 В кристалле исландского шпата имеется
единственное направление, вдоль
которого двойное лучепреломление не
наблюдается. Направление в оптически
анизотропном кристалле, по которому
луч света распространяется, не испытывая
двойного лучепреломления, называется
оптической
осью кристалла.
В данном случае речь идет именно о
направлении,
а не о прямой линии, проходящей через
какую-то точку кристалла. Любая
прямая, проходящая параллельно данному
направлению, является оптической осью
кристалла.
Кристаллы в зависимости от типа их
симметрии бывают одноосные и двуосные,
т.е. имеют одну или две оптические оси
(к первым и относится исландский шпат).
Исследования показывают, что вышедшие
из кристалла лучи плоскополяризованы
во взаимно перпендикулярных плоскостях.
Плоскость, проходящая через направление
луча света и оптическую ось кристалла,
называется главной
плоскостью
(или главным
сечением
кристалла). Колебания светового вектора
(вектора напряженности Е
электрического поля) в обыкновенном
луче происходят перпендикулярно
главной плоскости, в необыкновенном
— в главной плоскости (рис. 278).
Неодинаковое преломление обыкновенного
и необыкновенного лучей указывает на
различие для них показателей преломления.
Очевидно, что при любом направлении
обыкновенного луча колебания светового
вектора перпендикулярны оптической
оси кристалла, поэтому обыкновенный
луч распространяется по всем направлениям
с одинаковой скоростью и, следовательно,
показатель преломления no
для него есть величина постоянная.
Для необыкновенного же луча угол между
направлением колебаний светового
вектора и оптической осью отличен от
прямого и зависит от направления луча,
поэтому необыкновенные лучи
распространяются по различным
направлениям с разными скоростями.
Следовательно, показатель преломления
пe
необыкновенного луча является
переменной величиной, зависящей от
направления луча. Таким образом,
обыкновенный луч подчиняется закону
преломления (отсюда и название
«обыкновенный»), а для необыкновенного
луча этот закон не выполняется. После
выхода из кристалла, если не принимать
во внимание поляризацию во взаимно
перпендикулярных плоскостях, эти два
луча ничем друг от друга не отличаются.
Как уже рассматривалось, обыкновенные
лучи распространяются в кристалле по
всем направлениям с одинаковой
скоростью vo=c/no,
а необыкновенные — с разной скоростью
ve=с/пe
(в зависимости от угла между вектором
Е
и оптической осью). Для луча,
распространяющегося вдоль оптической
оси, no=ne,
vo=ve,
т.е. вдоль оптической оси существует
только одна скорость распространения
света. Различие в ve
и vo
для всех направлений, кроме направления
оптической оси, и обусловливает явление
двойного лучепреломления света в
одноосных кристаллах. Допустим, что
в точке S
внутри одноосного кристалла находится
точечный источник света. На рис.
279 показано распространение обыкновенного
и необыкновенного лучей в кристалле
(главная плоскость совпадает с
плоскостью чертежа, OO'
— направление
оптической оси). Волновой поверхностью
обыкновенного луча (он распространяется
с vo=const)
является сфера, необыкновенного луча
(veconst)
— эллипсоид вращения. Наибольшее
расхождение волновых поверхностей
обыкновенного и необыкновенного
лучей наблюдается в направлении,
перпендикулярном оптической оси.
Эллипсоид и сфера касаются друг друга
в точках их пересечения с оптической
осью OO'.
Если ve<vo
(ne>no),
то эллипсоид необыкновенного луча
вписан в сферу обыкновенного луча
(эллипсоид скоростей вытянут относительно
оптической оси) и
одноосный кристалл называется
положительным
(рис. 279, а).
Если ve>vo
(ne<no),
то эллипсоид описан вокруг сферы
(эллипсоид скоростей растянут в
направлении, перпендикулярном
оптической оси) и одноосный кристалл
называется отрицательным
(рис. 279, б).
Рассмотренный выше исландский шпат
относится к отрицательным кристаллам.
В качестве примера построения
обыкновенного и необыкновенного лучей
рассмотрим преломление плоской
волны на границе анизотропной среды,
например положительной (рис. 280).
Пусть свет падает нормально к
преломляющей грани кристалла, а
оптическая ось OO'
составляет с нею некоторый угол. С
центрами в точках А
и В
построим сферические волновые
поверхности, соответствующие
обыкновенному лучу, и эллипсоидальные
— необыкновенному лучу. В точке,
лежащей на OO',
эти поверхности соприкасаются.
Согласно принципу Гюйгенса, поверхность,
касательная к сферам, будет фронтом
(а—а)
обыкновенной волны, поверхность,
касательная к эллипсоидам, — фронтом
(b—b)
необыкновенной волны. Проведя к точкам
касания прямые, получим направления
распространения обыкновенного (о)
и необыкновенного (е)
лучей. Таким образом, в данном случае
обыкновенный луч пойдет вдоль
первоначального направления,
необыкновенный же отклонится от
первоначального направления.
В кристалле исландского шпата имеется
единственное направление, вдоль
которого двойное лучепреломление не
наблюдается. Направление в оптически
анизотропном кристалле, по которому
луч света распространяется, не испытывая
двойного лучепреломления, называется
оптической
осью кристалла.
В данном случае речь идет именно о
направлении,
а не о прямой линии, проходящей через
какую-то точку кристалла. Любая
прямая, проходящая параллельно данному
направлению, является оптической осью
кристалла.
Кристаллы в зависимости от типа их
симметрии бывают одноосные и двуосные,
т.е. имеют одну или две оптические оси
(к первым и относится исландский шпат).
Исследования показывают, что вышедшие
из кристалла лучи плоскополяризованы
во взаимно перпендикулярных плоскостях.
Плоскость, проходящая через направление
луча света и оптическую ось кристалла,
называется главной
плоскостью
(или главным
сечением
кристалла). Колебания светового вектора
(вектора напряженности Е
электрического поля) в обыкновенном
луче происходят перпендикулярно
главной плоскости, в необыкновенном
— в главной плоскости (рис. 278).
Неодинаковое преломление обыкновенного
и необыкновенного лучей указывает на
различие для них показателей преломления.
Очевидно, что при любом направлении
обыкновенного луча колебания светового
вектора перпендикулярны оптической
оси кристалла, поэтому обыкновенный
луч распространяется по всем направлениям
с одинаковой скоростью и, следовательно,
показатель преломления no
для него есть величина постоянная.
Для необыкновенного же луча угол между
направлением колебаний светового
вектора и оптической осью отличен от
прямого и зависит от направления луча,
поэтому необыкновенные лучи
распространяются по различным
направлениям с разными скоростями.
Следовательно, показатель преломления
пe
необыкновенного луча является
переменной величиной, зависящей от
направления луча. Таким образом,
обыкновенный луч подчиняется закону
преломления (отсюда и название
«обыкновенный»), а для необыкновенного
луча этот закон не выполняется. После
выхода из кристалла, если не принимать
во внимание поляризацию во взаимно
перпендикулярных плоскостях, эти два
луча ничем друг от друга не отличаются.
Как уже рассматривалось, обыкновенные
лучи распространяются в кристалле по
всем направлениям с одинаковой
скоростью vo=c/no,
а необыкновенные — с разной скоростью
ve=с/пe
(в зависимости от угла между вектором
Е
и оптической осью). Для луча,
распространяющегося вдоль оптической
оси, no=ne,
vo=ve,
т.е. вдоль оптической оси существует
только одна скорость распространения
света. Различие в ve
и vo
для всех направлений, кроме направления
оптической оси, и обусловливает явление
двойного лучепреломления света в
одноосных кристаллах. Допустим, что
в точке S
внутри одноосного кристалла находится
точечный источник света. На рис.
279 показано распространение обыкновенного
и необыкновенного лучей в кристалле
(главная плоскость совпадает с
плоскостью чертежа, OO'
— направление
оптической оси). Волновой поверхностью
обыкновенного луча (он распространяется
с vo=const)
является сфера, необыкновенного луча
(veconst)
— эллипсоид вращения. Наибольшее
расхождение волновых поверхностей
обыкновенного и необыкновенного
лучей наблюдается в направлении,
перпендикулярном оптической оси.
Эллипсоид и сфера касаются друг друга
в точках их пересечения с оптической
осью OO'.
Если ve<vo
(ne>no),
то эллипсоид необыкновенного луча
вписан в сферу обыкновенного луча
(эллипсоид скоростей вытянут относительно
оптической оси) и
одноосный кристалл называется
положительным
(рис. 279, а).
Если ve>vo
(ne<no),
то эллипсоид описан вокруг сферы
(эллипсоид скоростей растянут в
направлении, перпендикулярном
оптической оси) и одноосный кристалл
называется отрицательным
(рис. 279, б).
Рассмотренный выше исландский шпат
относится к отрицательным кристаллам.
В качестве примера построения
обыкновенного и необыкновенного лучей
рассмотрим преломление плоской
волны на границе анизотропной среды,
например положительной (рис. 280).
Пусть свет падает нормально к
преломляющей грани кристалла, а
оптическая ось OO'
составляет с нею некоторый угол. С
центрами в точках А
и В
построим сферические волновые
поверхности, соответствующие
обыкновенному лучу, и эллипсоидальные
— необыкновенному лучу. В точке,
лежащей на OO',
эти поверхности соприкасаются.
Согласно принципу Гюйгенса, поверхность,
касательная к сферам, будет фронтом
(а—а)
обыкновенной волны, поверхность,
касательная к эллипсоидам, — фронтом
(b—b)
необыкновенной волны. Проведя к точкам
касания прямые, получим направления
распространения обыкновенного (о)
и необыкновенного (е)
лучей. Таким образом, в данном случае
обыкновенный луч пойдет вдоль
первоначального направления,
необыкновенный же отклонится от
первоначального направления.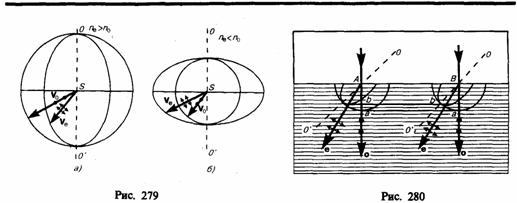
|
54.Вращение
плоскости поляризации.
Некоторые вещества (например, из
твердых тел — кварц, сахар, киноварь,
из жидкостей — водный раствор сахара,
винная кислота, скипидар), называемые
оптически активными,
обладают способностью вращать плоскость
поляризации. Вращение плоскости
поляризации можно наблюдать на
следующем опыте (рис. 285). Если между
скрещенными поляризатором Р
и анализатором А,
дающими темное поле зрения, поместить
оптически активное вещество (например,
кювету с раствором сахара), то поле
зрения анализатора просветляется.
При повороте анализатора на некоторый
угол
можно вновь получить темное поле
зрения. Угол
и есть угол,
на который оптически активное вещество
поворачивает плоскость поляризации
света, прошедшего через поляризатор.
Так как поворотом анализатора можно
получить темное поле зрения, то свет,
прошедший через оптически активное
вещество, является плоско поляризованным.
Опыт показывает, что угол поворота
плоскости поляризации для оптически
активных кристаллов и чистых жидкостей
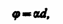 для
оптически активных растворов для
оптически активных растворов
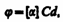 (196.1) где d
— расстояние, пройденное светом в
оптически активном веществе, ([])
— так называемое удельное
вращение,
численно равное углу поворота плоскости
поляризации света слоем оптически
активного вещества единичной толщины
(единичной концентрации — для
растворов), С
— массовая концентрация оптически
активного вещества в растворе, кг/м3.
Удельное вращение зависит от природы
вещества, температуры и длины волны
света в вакууме. Опыт показывает, что
все вещества, оптически активные в
жидком состоянии, обладают таким же
свойством и в кристаллическом состоянии.
Однако если вещества активны в
кристаллическом состоянии, то не
всегда активны в жидком (например,
расплавленный кварц). Следовательно,
оптическая активность обусловливается
как строением молекул вещества (их
асимметрией), так и особенностями
расположения частиц в кристаллической
решетке. Оптически
активные
вещества
в зависимости от направления вращения
плоскости поляризации разделяются
на право-
и левовращающие.
В первом случае плоскость поляризации,
если смотреть навстречу лучу, вращается
вправо (по часовой стрелке), во втором
— влево (против часовой стрелки).
Вращение плоскости поляризации
объяснено О. Френелем (1817 г.). Согласно
теории Френеля, скорость распространения
света в оптически активных веществах
различна для лучей, поляризованных
по кругу вправо и влево. Явление
вращения плоскости поляризации и, в
частности, формула (196.1) лежат в основе
точного метода определения концентрации
растворов оптически активных веществ,
называемого поляриметрией
(сахариметрией).
Для этого используется установка,
показанная на рис. 285. По найденному
углу поворота плоскости поляризации
и известному значению []
из (196.1) находится концентрация
растворенного вещества. Впоследствии
М. Фарадеем было обнаружено вращение
плоскости поляризации в оптически
неактивных телах, возникающее под
действием магнитного поля. Это явление
получило название эффект
Фарадея
(или магнитного
вращения плоскости поляризации).
Оно имело огромное значение для науки,
так как было первым явлением, в котором
обнаружилась связь между оптическими
и электромагнитными процессами.
(196.1) где d
— расстояние, пройденное светом в
оптически активном веществе, ([])
— так называемое удельное
вращение,
численно равное углу поворота плоскости
поляризации света слоем оптически
активного вещества единичной толщины
(единичной концентрации — для
растворов), С
— массовая концентрация оптически
активного вещества в растворе, кг/м3.
Удельное вращение зависит от природы
вещества, температуры и длины волны
света в вакууме. Опыт показывает, что
все вещества, оптически активные в
жидком состоянии, обладают таким же
свойством и в кристаллическом состоянии.
Однако если вещества активны в
кристаллическом состоянии, то не
всегда активны в жидком (например,
расплавленный кварц). Следовательно,
оптическая активность обусловливается
как строением молекул вещества (их
асимметрией), так и особенностями
расположения частиц в кристаллической
решетке. Оптически
активные
вещества
в зависимости от направления вращения
плоскости поляризации разделяются
на право-
и левовращающие.
В первом случае плоскость поляризации,
если смотреть навстречу лучу, вращается
вправо (по часовой стрелке), во втором
— влево (против часовой стрелки).
Вращение плоскости поляризации
объяснено О. Френелем (1817 г.). Согласно
теории Френеля, скорость распространения
света в оптически активных веществах
различна для лучей, поляризованных
по кругу вправо и влево. Явление
вращения плоскости поляризации и, в
частности, формула (196.1) лежат в основе
точного метода определения концентрации
растворов оптически активных веществ,
называемого поляриметрией
(сахариметрией).
Для этого используется установка,
показанная на рис. 285. По найденному
углу поворота плоскости поляризации
и известному значению []
из (196.1) находится концентрация
растворенного вещества. Впоследствии
М. Фарадеем было обнаружено вращение
плоскости поляризации в оптически
неактивных телах, возникающее под
действием магнитного поля. Это явление
получило название эффект
Фарадея
(или магнитного
вращения плоскости поляризации).
Оно имело огромное значение для науки,
так как было первым явлением, в котором
обнаружилась связь между оптическими
и электромагнитными процессами.
|
55.Дисперсия
света.
Групповая скорость.Дисперсия
света зависимость
показателя преломления n
вещества от частоты ν (длины волны λ)
света или зависимость фазовой скорости
(См. Фазовая
скорость) световых волн от частоты.
Следствие Д. с. — разложение в спектр
пучка белого света при прохождении
сквозь призму (см. Спектры
оптические). Изучение этого спектра
привело И. Ньютона (1672) к открытию Д.
с. Для веществ, прозрачных в данной
области спектра, n
увеличивается
с увеличением ν (уменьшением λ), чему
и соответствует распределение цветов
в спектре; такая зависимость n
от λ называется нормальной Д. с. Вблизи
полос поглощения вещества ход изменения
n
с длиной волны значительно сложнее.
Так, для тонкой призмы из красителя
цианина (рис.
1) в области
поглощения красные лучи преломляются
сильнее фиолетовых, а наименее
преломляемым будет зелёный, затем
синий (так называемая аномальная Д.
с.). У всякого вещества имеются свои
полосы поглощения, и общий ход показателя
преломления обусловлен распределением
этих полос по спектру. На рис.
2 показан
вид интерференционных полос в области
аномальной дисперсии паров натрия.
Преломление света в веществе возникает
вследствие изменения фазовой скорости
света; показатель преломления n = c0/c,
где c0
— скорость света в вакууме, с
— фазовая скорость его в данной среде.
По электромагнитной теории света
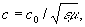 где
ε — диэлектрическая проницаемость,
μ — магнитная проницаемость. В
оптической области спектра для всех
веществ μ очень близко к 1. Поэтому где
ε — диэлектрическая проницаемость,
μ — магнитная проницаемость. В
оптической области спектра для всех
веществ μ очень близко к 1. Поэтому
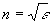 и
Д. с. объясняется зависимостью ε от
частоты. Эта зависимость связана с
взаимодействием электромагнитного
поля световой волны с атомами и
молекулами, приводящим к поглощению;
показатель преломления при этом
становится комплексной величиной и
Д. с. объясняется зависимостью ε от
частоты. Эта зависимость связана с
взаимодействием электромагнитного
поля световой волны с атомами и
молекулами, приводящим к поглощению;
показатель преломления при этом
становится комплексной величиной
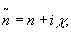 где
χ характеризует поглощение. В видимой
и ультрафиолетовой областях спектра
основное значение имеют колебания
электронов, а в инфракрасной — колебания
ионов. Согласно
классическим представлениям, под
действием электрического поля световой
волны электроны атомов или молекул
совершают вынужденные колебания с
частотой, равной частоте приходящей
волны. При приближении частоты световой
волны к частоте собственных колебаний
электронов возникает явление Резонанса,
обусловливающее зависимость ε от
частоты, а также поглощение света. Эта
теория хорошо объясняет связь Д. с. с
полосами поглощения. Для того чтобы
получить количественное совпадение
с опытом, в классической теории
приходилось вводить для каждой линии
поглощения некоторые эмпирические
константы («силы осцилляторов»).
Согласно электронной теории, справедливы
приближённые формулы: где
χ характеризует поглощение. В видимой
и ультрафиолетовой областях спектра
основное значение имеют колебания
электронов, а в инфракрасной — колебания
ионов. Согласно
классическим представлениям, под
действием электрического поля световой
волны электроны атомов или молекул
совершают вынужденные колебания с
частотой, равной частоте приходящей
волны. При приближении частоты световой
волны к частоте собственных колебаний
электронов возникает явление Резонанса,
обусловливающее зависимость ε от
частоты, а также поглощение света. Эта
теория хорошо объясняет связь Д. с. с
полосами поглощения. Для того чтобы
получить количественное совпадение
с опытом, в классической теории
приходилось вводить для каждой линии
поглощения некоторые эмпирические
константы («силы осцилляторов»).
Согласно электронной теории, справедливы
приближённые формулы:
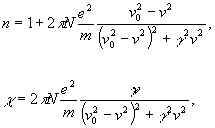 где
N
— число частиц в единице объёма, е
и m
— заряд и масса электрона, γ —
коэффициент затухания. На рис.
3 приведены
графики зависимости n и χ от ν/ν0.
Квантовая
теория подтвердила качественные
результаты классической теории и,
кроме того, дала возможность связать
эти константы с другими характеристиками
электронных оболочек атомов (их
волновыми функциями в разных
энергетических состояниях). Квантовая
теория объяснила также особенности
Д. с., наблюдающиеся в тех случаях,
когда имеется значительное число
атомов в возбуждённых состояниях (так
называемая отрицательная Д. с.). Д. с.
в прозрачных материалах, применяемых
в оптических приборах, имеет большое
значение при расчёте спектральных
приборов в целях получения хороших
спектров, при расчёте ахроматических
линз или призм, для уничтожения Д. с.,
вызывающей хроматическую аберрацию.
ГРУППОВА́Я СКО́РОСТЬ, величина,
приближенно характеризующая
распространение негармонической
волны (она является суперпозицией
группы гармонических волн). Если форма
волны изменяется в результате дисперсии
волн в среде не очень быстро, то можно
рассматривать распространение
негармонической волны как целого с
групповой скоростью, отличной от
фазовых скоростей ее гармонических
составляющих. Групповая скорость
характеризует скорость переноса
энергии волной. где
N
— число частиц в единице объёма, е
и m
— заряд и масса электрона, γ —
коэффициент затухания. На рис.
3 приведены
графики зависимости n и χ от ν/ν0.
Квантовая
теория подтвердила качественные
результаты классической теории и,
кроме того, дала возможность связать
эти константы с другими характеристиками
электронных оболочек атомов (их
волновыми функциями в разных
энергетических состояниях). Квантовая
теория объяснила также особенности
Д. с., наблюдающиеся в тех случаях,
когда имеется значительное число
атомов в возбуждённых состояниях (так
называемая отрицательная Д. с.). Д. с.
в прозрачных материалах, применяемых
в оптических приборах, имеет большое
значение при расчёте спектральных
приборов в целях получения хороших
спектров, при расчёте ахроматических
линз или призм, для уничтожения Д. с.,
вызывающей хроматическую аберрацию.
ГРУППОВА́Я СКО́РОСТЬ, величина,
приближенно характеризующая
распространение негармонической
волны (она является суперпозицией
группы гармонических волн). Если форма
волны изменяется в результате дисперсии
волн в среде не очень быстро, то можно
рассматривать распространение
негармонической волны как целого с
групповой скоростью, отличной от
фазовых скоростей ее гармонических
составляющих. Групповая скорость
характеризует скорость переноса
энергии волной.
|
|
56.Поглощение
света. уменьшение
интенсивности оптического излучения
(света),
проходящего через материальную среду,
за счёт процессов его взаимодействия
со средой. Световая энергия при П. с.
переходит в различные формы внутренней
энергии среды; она может быть полностью
или частично переизлучена средой на
частотах, отличных от частоты
поглощённого излучения.
Экспериментально
было установлено, что свет, проходя
через вещество поглощается. Особенно
сильное поглощение наблюдается для
тех длин волн, частоты которых совпадают
с собственными частотами для данного
вещества. Интенсивность света изменяется
по закону: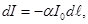 где
α – коэффициент поглощения,I0
– интенсивность
падающего света, где
α – коэффициент поглощения,I0
– интенсивность
падающего света,
 -
толщина поглощающего слоя.Знак минус
показывает, что dI
и -
толщина поглощающего слоя.Знак минус
показывает, что dI
и
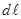 имеют
противоположные знаки, т.е. с ростом
толщины поглощающего слоя интенсивность
прошедшего света падает. имеют
противоположные знаки, т.е. с ростом
толщины поглощающего слоя интенсивность
прошедшего света падает.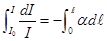 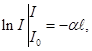 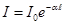 -
закон Бугера Если -
закон Бугера Если
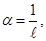 то
то
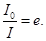 Коэффициент поглощения α есть величина
обратная величине пути в данном
веществе, проходя который, свет
уменьшает свою интенсивность в е
раз. Если растворить поглощающие свет
вещество в растворителе, который не
поглощает данный цвет, то коэффициент
поглощения раствора будет прямо
пропорционален длине поглощающего
вещества, т.е.
Коэффициент поглощения α есть величина
обратная величине пути в данном
веществе, проходя который, свет
уменьшает свою интенсивность в е
раз. Если растворить поглощающие свет
вещество в растворителе, который не
поглощает данный цвет, то коэффициент
поглощения раствора будет прямо
пропорционален длине поглощающего
вещества, т.е.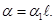 Для
разряженных газов спектр поглощения
является линейчатым. Для газа в
молекулярном состоянии спектр
поглощения является полосатым. Для
твердых диэлектриков спектр поглощения
сплошной в определенном интервале
частот. Все другие частоты диэлектрик
будет пропускать. Для
разряженных газов спектр поглощения
является линейчатым. Для газа в
молекулярном состоянии спектр
поглощения является полосатым. Для
твердых диэлектриков спектр поглощения
сплошной в определенном интервале
частот. Все другие частоты диэлектрик
будет пропускать.
|
57.
Рассеяние света.
Рассеивание
света или
другого электромагнитного
излучения
— вариант распространения лучей в
случайных направлениях, связанный с
взаимодействием излучения и вещества,
а также с неоднородностями в среде
или на поверхности, или передачи
излучения волн между двумя системами.
Рассеивание при отражении от неоднородной
поверхности называется диффузным
рассеянием.
Большинство объектов, которые каждый
видит, видимо должны осветить и
рассмотреть (отражение) в виде
рассеивания лучей от их поверхностей.
Кроме того, это первичный механизм
физического наблюдения.[3][4]Рассеивание
света зависит от длины волны или
частоты рассеиваемого света. Так как
видимый свет имеет длину волны при
рассмотрении величиной в микрон,
намного меньшие длины волн не могут
быть замечены даже при помощи микроскопа.
Коллоидные частицы всего в 1 мкм дали
возможность рассмотреть и отфильтровать
непосредственно в водной среде.
Передача различных частот света важна
в границах от стекла окна (оборудования
или стратегических объектов) к волокну
оптических кабелей,
а также при передаче сигналов в ракетных
системах обнаружения с наведением по
тепловому лучу с использованием
инфракрасных
лучей
(ИК). Передача световой энергии через
оптическую систему может быть уменьшена
поглощением, отражением и рассеиванием.
Рассеяние
Рэлея
- упругое рассеивание света или другого
электромагнитного излучения объектами
или поверхностями, намного меньшими,
чем длина волны падающего света. Это
часто может происходить на прозрачных
твердых частицах и жидкостях, но более
распространено в газах. Этот тип
рассеяния происходит в лучах синего
цвета
неба в течение дня. Рассеяние Рэлея
обратно пропорционально четвертой
степени длины волны, что означает, что
более короткая длина волны синего
света будет рассеяна более сильно,
чем более длинные длины волны (например,
зеленый и красный цвета). Это придаёт
небу синюю окраску. Рассеяние
Ми
рассеивается в виде лучей света
сферическими частицами. Рассеяние
Рэлея-Ми,
рассеивающий в специальном случае,
где диаметр частиц является намного
меньшим, чем длина волны света. Рассеяние
Мандельштама-Бриллюэна
может следовать из взаимодействия
легких фотонов с акустическими или
вибрационными квантами
(фононы). Рассеивание вызвано дифракцией
в плоскости монохроматических световых
волн непосредственными, синусоидальными
колебаниями плотности (то есть
постоянные тепловые, звуковые волны
или акустические фононы). Световая
волна, как полагают, рассеяна максимумом
плотности или амплитудой акустического
фонона, в той же самой манере в случае,
когда рентгеновские лучи рассеяны
кристаллическими частицами в теле.
Роль кристаллических элементов в этом
процессе походит на вид колебаний
плотности или звуковых волн в средах.
Взаимодействие состоит из неэластичного
процесса рассеивания, в котором фонон
или создан или уничтожен. Энергия (и
таким образом частота) рассеянного
света немного увеличена или уменьшена.
Раман-рассеяние подобно рассеянию
Мандельштама-Бриллюэна в тех обоих
случаях, представляют неэластичные
процессы рассеивания света. Различие
находится в обнаруженном диапазоне
изменения частоты и типе информации,
извлеченной из образца. При Раман—рассеянии
фотоны рассеяны косвенно с вибрационными
и вращательными переходами в молекулах.
Спектроскопия Raman поэтому используется,
чтобы определить химический состав
и молекулярную структуру, в то же время
как Рассеяние Мандельштама-Бриллюэна
измеряет свойства в большем масштабе,
т.е. типа упругого поведения.
|
|
|
|
|
|
|
|
|
|


 Когерентные
лучи 1′
и 1′′
дают интерференционную картину в
точке А', которая определяется разностью
хода этих лучей и будет зависеть от
толщины h
клина в месте падения на него луча.
Лучи 2′
и 2′′
собираются линзой в точке А′′.
Оптическая разность хода определяется
толщиной h'
.
Таким образом, на экране наблюдаются
интерференционные полосы. Каждая из
полос возникает за счет отражения от
мест пластинки, имеющих одинаковую
толщину. Интерференционные полосы на
поверхности пленки имеют одинаковую
освещенность на всех точках поверхности,
соответствующих одинаковым толщинам
пленки, и называются полосами
равной толщины.
Примером полос равной толщины являются
кольца Ньютона, которые наблюдаются
при отражении света от воздушного
зазора, образованного плоскопараллельной
пластинкой и соприкасающейся с ней
плосковыпуклой линзой с большим
радиусом кривизны (рис. 17.11, а). Воздушная
прослойка постепенно утолщается от
точки соприкосновения линзы к краям.
Отраженные от верхней и нижней границ
воздушной прослойки световые волны
интерферируют между собой. При этом
получается следующая картина: в точке
соприкосновения наблюдается черное
пятно, окруженное рядом концентрических
световых и черных колец убывающей
ширины (рис. 17.11, б).
Когерентные
лучи 1′
и 1′′
дают интерференционную картину в
точке А', которая определяется разностью
хода этих лучей и будет зависеть от
толщины h
клина в месте падения на него луча.
Лучи 2′
и 2′′
собираются линзой в точке А′′.
Оптическая разность хода определяется
толщиной h'
.
Таким образом, на экране наблюдаются
интерференционные полосы. Каждая из
полос возникает за счет отражения от
мест пластинки, имеющих одинаковую
толщину. Интерференционные полосы на
поверхности пленки имеют одинаковую
освещенность на всех точках поверхности,
соответствующих одинаковым толщинам
пленки, и называются полосами
равной толщины.
Примером полос равной толщины являются
кольца Ньютона, которые наблюдаются
при отражении света от воздушного
зазора, образованного плоскопараллельной
пластинкой и соприкасающейся с ней
плосковыпуклой линзой с большим
радиусом кривизны (рис. 17.11, а). Воздушная
прослойка постепенно утолщается от
точки соприкосновения линзы к краям.
Отраженные от верхней и нижней границ
воздушной прослойки световые волны
интерферируют между собой. При этом
получается следующая картина: в точке
соприкосновения наблюдается черное
пятно, окруженное рядом концентрических
световых и черных колец убывающей
ширины (рис. 17.11, б).
