3.4. Многомерная безградиентная оптимизация.

Концепция методов

Рассматриваются численные методы опти­мизации, у которых величина и направление шага к оптимуму формируются однозначно по определенным функциям в зависимости от свойств критерия оптимальности в окрестности текущей точки без использования производных (т.е. градиента). Все алгоритмы имеют итерационный характер и вы­ражаются формулой

Основная особенность рассматриваемой группы методов — отсутствие вычисления градиента критерия оптимальности. Ряд методов прямого поиска ба­зируется на последователь­ном применении одномер­ного поиска по переменным или по другим задаваемым направлениям, что облегча­ет их алгоритмизацию и применение.

Как и для градиентных методов, на рис. 18 приво­дятся лишь по одной из воз­можных траекторий поиска каждым из ниже рассмат­риваемых методов. Кроме того, также для всех приве­денных траекторий выбра­ны различные начальные условия, с тем, чтобы не за­громождать построения.

Основные методы

Метод Гаусса – Зайделя.

Метод Гаусса — Зайделя (в математической литературе ис­пользуется и другое название — метод покоординатного спуска) заключается в последовательном поиске оптимума R(x) поочередно по каждой переменной. Причем после завершения перебои на всех переменных (т.е. после завершения одного цикла) опять в общем случае приходится перебирать все переменные до тех пор, пока не придем к оптимуму.

Метод обладает низкой эффективностью в овражных функциях, может застревать в "ловушках", особенно при сравнительно больших шагах h при поиске оптимума по каждой переменной, очень чувствителен и к выбору системы координат. Метод прост в реализации. На эффективность метода влияет порядок чередования переменных.

Условием окончания поиска является малость изменения критерия оптимальности за один цикл или невозможность улучшения критерия оптимальности ни по одной из переменных.

При нахождении оптимума по каждой переменной прекращают поиск не в точке оптимума, а несколько пройдя ее. При этом удается "выскочить из ловушек", за меньшее число циклов выйти и район оптимума. В районе оптимума наблюдается зациклива­ние, и в этом случае последовательно уменьшают величину по­следействия.

В двумерных задачах метод Гаусса — Зайделя фактически сводится к методу наискорейшего спуска, так как в обоих методах траектория поиска представляет собой последовательность взаимноортогональных отрезков.

Симплексный метод.

Симплексом в n -мерном пространстве называют фигуру, со­держащую n +1 вершину. На плоскости — это треугольник, в трехмерном пространстве — тетраэдр и т.д. Если все вершины симплекса равно удалены друг от друга, то такой симплекс назы­вается регулярным. В литературе можно встретить и другое название метода — метод деформируемого многогранника. В организации алгоритма поиска используется важное свойство симплекса: против каждой вершины находится только одна грань. Суть метода заключается в следующем. В окрестности начальной точки х° строим симплекс, затем находится самая "пло­хая" его вершина (т.е. та, в которой наихудшее значение критерия оптимальности) и на противоположной грани строится новый симплекс, отличающийся от исходного только одной вершиной. Эта вершина получается симметричным отражением выбрасы­ваемой вершины относительно центра противолежащей грани. Центр грани определяется геометрически, как среднее значение по каждой проекции из всех вершин грани. Алгоритм получения новой вершины записывается следующим образом:

где х¹, х², ... — вектора вершины симплекса (координаты вер­шин), x^j — вектор выбрасываемой вершины, x^j — новая верши­на в новом симплексе. В скалярном представлении для каждой координаты будет аналогичная формула.

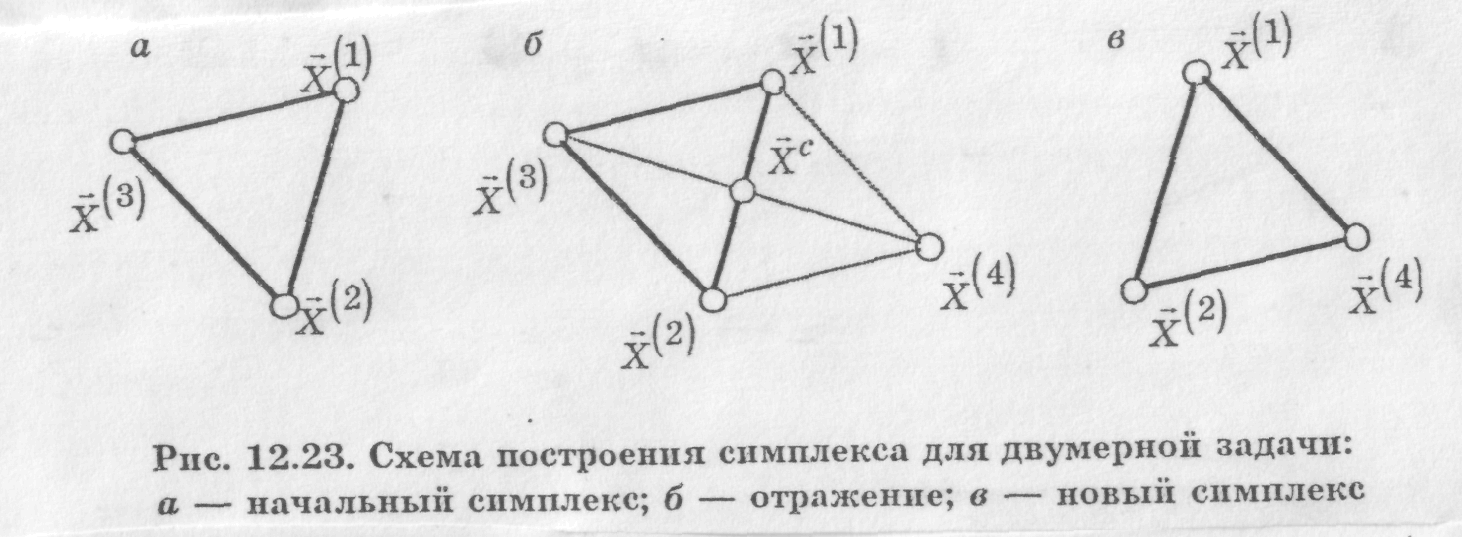
После построения нового симплекса требуется лишь одно вы­числение критерия оптимальности: только в новой вершине, так как в остальных углах они вычислены. Далее все повторяется сно­ва.

При выходе в район оптимума процесс поиска «зацикливается». Это имеет место тогда, когда приходится выбрасывать только что полученную вершину (если значение критерия в новой вершине оказывается самое плохое). В этом случае можно «сжимать» симплекс, откладывая новую вершину от грани на расстояние вдвое меньше, чем необходимо.

Х^j = 3/(2n) (x¹+x²+…xⁿ⁺¹) – (1+3/(2n))x^j.

Процесс сжатия происходит многократно, до тех пор пока размеры симплекса не будут меньше заданных.

Пример.

1. Требуется найти минимум функции , где А=1; В=2; С=1,2;D=2.

2. Интервал поиска: х_1нач=2, х_1кон= 2, х_2нач=2, х_2кон= 2.

3. Начальная точка: х₁₀= 1,4962, х₂₀=1.

4. Параметры поиска: шаг h=0,5, погрешность = 0,01.

В окрестности заданной начальной точки (1,4962, 1,0000), R=3,9719 сформируем начальный симплекс, его координатами являются:

№вершины	х1	х2	R
1	1,7462	0,8557	4,1938
2	1,2462	0,8557	1,7519
3	1,4962	1,2887	6,7368

Конечно, можно и по-другому построить начальный симплекс, например, заданная начальная точка может являться одной из вершин симплекса, а не лежать внутри симплекса, как в данном случае. Это не принципиально и на результат существенно не влияет.

Не трудно заметить, что самой плохой вершиной является третья (самое большое значение критерия). Удалим эту вершину и на противоположной грани построим новый симплекс. Практически это означает, что нужно найти одну вершину нового симплекса. Применим базовый алгоритм для каждой переменной х₁ и х₂ отдельно.

Получим новую вершину:

№вершины	х1	х2	R
4	1,4962	0,4226	0,8839

Теперь симплекс образуют вершины 1, 2, 4. Самая плохая вершина – 4. По аналогичной формуле перейдём к следующей новой вершине, «отразив» удаляемую относительно центра грани.

Получим вершину:

№вершины	х1	х2	R
5	0,9962	0,4226	0,4578

Теперь симплекс образуют вершины 2, 4, 5. Самая плохая вершина – 2. Строим следующую вершину:

№вершины	х1	х2	R
6	1,2462	0,0104	1,5919

Оказалось, что только что полученную вершину нужно будет удалять как самую плохую. Следовательно, необходимо сжимать симплекс, воспользовавшись второй формулой алгоритма.

№вершины	х1	х2	R
7	1,2462	0,6392	0,8750

Далее приведём без комментариев координаты вершин следующих симплексов, предоставив учащимся самостоятельно определять самую плохую вершину в каждом текущем симплексе.

№вершины	х1	х2	R
8	0,7462	0,6392	0,6435	отражение
9	0,4962	0,4226	0,3610	отражение
10	0,7462	0,2061	0,3707	отражение
11	0,2462	0,2061	0,1157	отражение
…	…	…	…	…
15	0,4962	0,0104	0,2526	отражение
16	0,0663	0,1520	0,0490	сжатие
17	0,3163	0,0645	0,1238	отражение
18	0,1056	0,1385	0,0458	сжатие
…	…	…	…	…
24	0,0089	0,0704	0,0100	отражение
25	0,1014	0,0814	0,0256	отражение
26	0,0546	0,0199	0,0039	сжатие

Симплекс быстро сжимается вокруг искомой оптимальной точки.

При выходе в район оптимума процесс поиска "зацикливает­ся". Это имеет место тогда, когда приходится выбрасывать только что полученную вершину (эта ситуация возникает в том случае, если значение критерия в новой вершине оказывается самое пло­хое). В этом случае можно "сжимать" симплекс, откладывая но­вую вершину от грани на расстоянии вдвое меньше, чем необхо­димо.

Процесс сжатия происходит многократно, до тех пор, пока размеры симплекса не будут меньше заданных или пока наиболь­шее расстояние между вершинами симплекса (длина ребра) не бу­дет меньше заданной величины.

Под размерами симплекса пони­мается расстояние от его центра до всех вершин (в этом случае расстояние от центра до всех вершин должно быть меньше задан­ного), а иногда и периметр симплекса, т.е. сумма всех его ребер.

Основным недостатком метода является невозможность уско­рения поиска вдали от оптимума. Этот недостаток устранен в од­ной из модификаций метода, известной как метод Нелдера — Мида. В этом варианте симплексного метода предусмотрено рас­тяжение симплекса в случае, если новая вершина лучше лучшей в старом симплексе, а также сжатия симплекса, если новая вершина оказывается хуже наихудшей в старом симплексе.

Имеется также операция уменьшения размера симплекса, называемая редукцией, которая вводится в случае зацикливания. При этом уменьшаются все грани симплекса одновременно в два раза. Уменьшение размера симплекса в два раза осуществляется делением пополам расстояния от каждой точки симплекса до точки х₁ определяющей наименьшее значение функции, т.е. будет: x_i = x_i^c+0,5(x_i - x₁).

КОНТРОЛЬНЫЕ ВОПРОСЫ

Метод Гаусса—Зайделя

1. Достаточно ли провести поиск оптимума поочередно по всем переменным последовательно?

2. Область наиболее предпочтительного использования метода Гаусса — Зайделя.

3. Может ли оказывать влияние на результат поиска (значение оптимума) порядок чередования переменных при поиске?

4. Может ли оказывать влияние на эффективность поиска поря­док чередования переменных?

5. Условие окончания поиска min R (x).

6. Основное достоинство метода.

7. Основной недостаток метода.

Симплексный метод

1. Что называется симплексом?

2. Как находится вершина нового (следующего) симплекса?

3. Признак зацикливания симплексного поиска.

4. Условие растяжения симплекса в процессе поиска.

5. Алгоритм сжатия симплекса в процессе поиска в одной из мо­дификаций.

6. Условие окончания поиска.

7. Как находится точка, относительно которой отражается но­вая вершина следующего симплекса?