
- •Кинематика материальной точки. Системы отсчета. Траектория, перемещение, путь, скорость, ускорение. Равномерное и равнопеременное прямолинейные движения.
- •Криволинейное движение. Нормальное и тангенциальное ускорения.
- •Траектория, путь, перемещение, линейная скорость, линейное ускорение.
- •Частные случаи движения
- •Движение точки по окружности. Угловые перемещение, скорость, ускорение. Связь между линейными и угловыми характеристиками.
- •Угол поворота, угловая скорость, угловое ускорение.
- •Связь между линейными и угловыми характеристиками
- •Динамика материальной точки. Инерциальные системы отсчета и первый закон Ньютона
- •Первый закон Ньютона (закон инерции)
- •Фундаментальные взаимодействия. Силы различной природы (упругие, гравитационные, трения), второй закон Ньютона. Масса. Третий закон Ньютона.
- •Динамические характеристики поступательного движения
- •Импульс () векторная величина, равная произведению массы тела на его скорость, характеризует способность механического движения передаваться от одного тела к другому.
- •Импульс силы () векторная величина, численно равная произведению силы на время ее действия и совпадающая по направлению с направлением силы. Второй закон Ньютона
- •Главный вектор системы или равнодействующая (результирующая) сила; n количество сил. Третий закон Ньютона
- •Импульс системы материальных точек, уравнение движения центра масс. Закон сохранения импульса. Закон сохранения импульса для механической системы
- •3. Моментом импульса материальной точки относительно точки о называется векторное произведение радиуса-вектора материальной точки на ее импульс
- •Уравнение моментов
- •Закон сохранения момента импульса
- •Работа при вращательном движении
- •Мощность при поступательном и вращательном движении
- •Кинетическая энергия
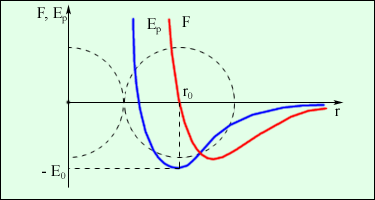
- •Потенциальная энергия
- •Потенциальная энергия в поле сил тяжести
- •Потенциальная энергия в поле упругих сил
- •Закон сохранения механической энергии
- •9. Соударение тел. Упругое и неупругое взаимодействия
- •Абсолютно упругий центральный удар двух тел
- •Абсолютно неупругий центральный удар двух тел
- •Колебательное движение и его характеристики: смещение, амплитуда, фаза, циклическая частота, период, скорость, ускорение, сила, энергия
- •Кинематические и динамические характеристики свободных незатухающих колебаний
- •Векторные диаграммы для представления гармонических колебаний
- •Сложение параллельных колебаний одинаковой частоты. Биения.
- •Вынужденные колебания. Резонанс
- •14. Волновое движение. Уравнение плоской незатухающей бегущей волны. Энергия упругой волны. Вектор плотности потока энергии
- •Уравнение плоской бегущей волны
- •Фазовая скорость
- •Энергия упругой волны. Вектор Умова
- •Термодинамическая система. Параметры состояния термодинамической системы. Основные положения молекулярно - кинетической теории газов
- •Параметры состояния идеального газа
- •Молекулярно-кинетическая теория газов
- •16. Основное уравнение молекулярно-кинетической теории газов (уравнение Клаузиуса). Уравнение состояния идеального газа (Менделеева - Клапейрона) Уравнение Клаузиуса
- •Уравнение Менделеева - Клапейрона
- •Закон равномерного распределения энергии по степеням свободы молекул
- •Работа и теплота. Теплоемкость, ее виды
- •Виды теплоемкости
- •Первый закон термодинамики
- •Определение теплоемкостей Ср , сv
- •18. Основные термодинамические процессы идеального газа. Политропный процесс, его частные случаи: изобарный, изотермический, адиабатный, изохорный
- •Теплота в политропном процессе
- •Энтропия, второй закон термодинамики
Параметры состояния идеального газа
Состояние идеального газа характеризуется тремя параметрами:
давлением;
температурой;
удельным объемом (плотностью).
1. Давление скалярная величина, характеризующая отношение силы, действующей по нормали к площадке, к величине этой площадки
![]() ,
(1)
,
(1)
![]() ;
;
![]() .
.
2. Температура скалярная величина, характеризующая интенсивность хаотического поступательного движения молекул, и пропорциональная средней кинетической энергии этого движения.
![]() ,
,
![]() при
при![]() (2)
(2)
Температурные шкалы
Эмпирическая шкала
Цельсия ( t
0C):
10C
=
![]() 0C;
0C;
Эмпирическая шкала
Фаренгейта:
![]() .
.
Пример: t
= 36,60C;
![]() .
.
Абсолютная шкала
Кельвина:
![]()
Удельный объем (плотность)
![]() удельный объем
это объем вещества массой в 1 кг;
удельный объем
это объем вещества массой в 1 кг;
![]() плотность это
масса вещества объемом в 1 м3;
плотность это
масса вещества объемом в 1 м3;
![]() .
.
Молекулярно-кинетическая теория газов
1. Все вещества состоят из атомов или молекул, размеры которых порядка 10-10м.
2.Атомы и молекулы вещества разделены промежутками, свободными от вещества. Косвенным подтверждением этого факта является изменяемость объема тела.
Рис. 2
3.Между молекулами тела одновременно действуют силы взаимного протяжения и силы взаимного отталкивания.
Рис. 3

Скорость движения молекул связана с температурой тела в целом: чем больше эта скорость, тем выше температура. Таким образом, скорость движения молекул определяет тепловое состояние тела – его внутреннюю энергию.
16. Основное уравнение молекулярно-кинетической теории газов (уравнение Клаузиуса). Уравнение состояния идеального газа (Менделеева - Клапейрона) Уравнение Клаузиуса
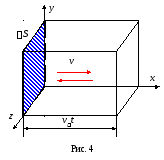 Вычислим
давление, оказываемое молекулами на
площадку S.
Вычислим
давление, оказываемое молекулами на
площадку S.
2-й закон Ньютона:
![]()
![]()
![]()
![]()
![]()
![]() . (1)
. (1)
Для одной молекулы:
![]() .
(2)
.
(2)
Число молекул в объеме параллелепипеда с основанием S и высотой vit:
N = niV = niSvit (3)
n = N/V – концентрация молекул, равная отношению числа молекул к объему занимаемого ими пространства.
Для молекул, которые передают импульс площадке S (в одном из трех взаимно перпендикулярных направлений движется 1/3 молекул, половина из них, т.е. 1/6 – на площадку S)
![]()
![]() средняя
квадратичная скорость молекул
средняя
квадратичная скорость молекул
![]()
![]()
![]() , (4)
, (4)
![]() средняя
кинетич. энергия поступательного
движения молекул
средняя
кинетич. энергия поступательного
движения молекул
Уравнение Клаузиуса: давление идеального газа численно равно 2/3 средней кинетической энергии поступательного движения молекул, находящихся в единичном объеме.
Уравнение Менделеева - Клапейрона
Это уравнение связывает параметры состояния р, Т, М, V.
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() уравнение
Менделеева – Клапейрона (5)
уравнение
Менделеева – Клапейрона (5)
1-й закон Авогадро: киломоли всех газов при нормальных условиях занимают одинаковый объем, равный 22,4 м3/кмоль. (Если температура газа равна T0 = 273,15 К (0 °С), а давление p0 = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях.)
![]()

Уравнение Менделеева – Клапейрона для 1 моля газа
![]() .
(6)
.
(6)
Уравнение Менделеева – Клапейрона для произвольной массы газа
![]() число молей.
число молей.
![]() ,
,
![]()
![]()
![]()
![]()
![]() (7)
(7)
Частные случаи уравнения Менделеева – Клапейрона
1.![]()
![]()
![]() изотермическое
состояние(закон Бойля – Мариотта)
изотермическое
состояние(закон Бойля – Мариотта)
2.![]()
![]()
![]() изобарное состояние(закон Гей-Люссака)
изобарное состояние(закон Гей-Люссака)
3.![]()
![]()
![]() изохорное состояние(закон Шарля)
изохорное состояние(закон Шарля)
17. Энергия термодинамической системы. Первый закон термодинамики. Работа, теплота, теплоемкость, ее виды
Энергия – это количественная мера движения материи.
![]() .
.
Внутренняя энергия системы U равна сумме всех видов энергий движения и взаимодействия частиц, составляющих данную систему.
Работа – это способ передачи энергии, связанный с изменением внешних параметров системы.
Теплота – это способ передачи энергии, связанный с изменением внутренних параметров системы.
Различия между теплотой и работой:
работа может неограниченно превращаться в любой вид энергии, превращение теплоты ограничено рамками 2-го закона термодинамики: она идет только на увеличение внутренней энергии;
работа связана с изменением внешних параметров системы, теплота – с изменением внутренних параметров.
Все три величины – энергия, работа и теплота – в системе СИ измеряются в джоулях (Дж).
