4.4. Критические нагрузки на грунт

Выше уже отмечалось, что по мере загружения фундамента наблюдаются две критические нагрузки: нагрузка, соответствующая началу возникновения в грунте зон сдвига и окончания фазы уплотнения, и нагрузка, при которой под нагруженным фундаментом сформировываются сплошные области предельного равновесия, грунт приходит в неустойчивое состояние, исчерпывается его несущая способность.

4.4.1. Начальная критическая нагрузка

Для произвольной точки М, расположенной на глубине z и характеризуемой углом видимости  (рис.4.6), рассмотрим условия возникновения предельного напряженного состояния. Главные напряжения с учетом действия собственного веса грунта как сплошной нагрузки будут равны:

, (4.13)

. (4.14)

Подставим эти значения в уравнение предельного равновесия

и учитывая, что, получим

. (4.15)

Эту формулу можно рассматривать как уравнение граничной области предельного равновесия, а z – как ординату этой области. Решая уравнение (4.15) относительно z, получим

. (4.16)

Максимальную глубину зоны сдвигов z_max определим, взяв производную z по  и приравняв ее к нулю:

. (4.17)

Это уравнение удовлетворяется, когда cos = sin или

; .

Подставляя полученные значения в выражение (4.16) и решая его относительно Р=Р_кр , получим критическое давление на глубине z

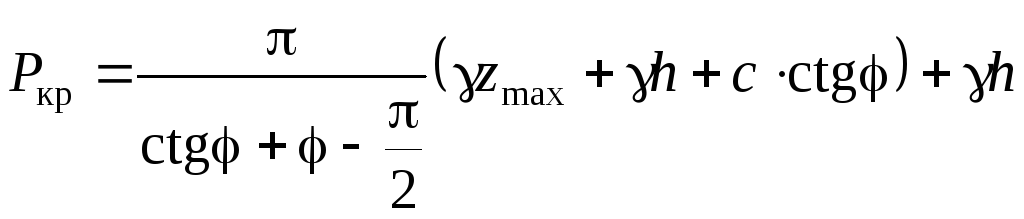; (4.18)

при z_max=0 находим начальную критическую нагрузку:

. (4.19)

Это формула Н.П.Пузыревского (пример 5). Строительные нормы СНиП 2.02.01-83 допускают развитие пластических деформаций в краевых участках фундаментов на глубину 1/4b. Тогда

P_кр1/4=R=. (4.20)

Это выражение можно привести к виду

, (4.21)

где , ,,

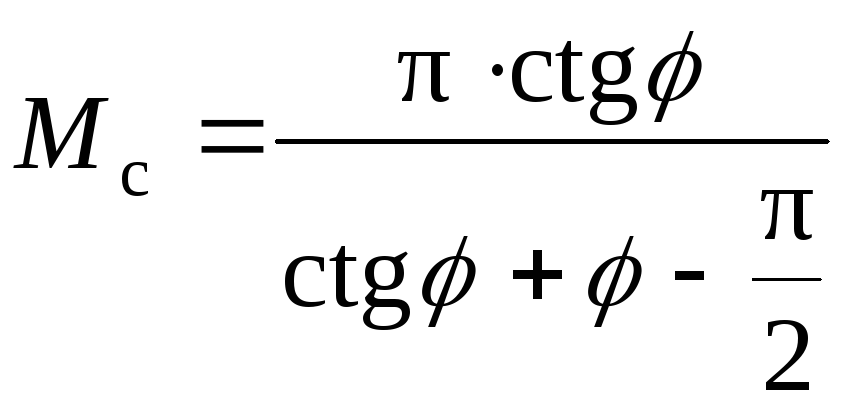здесь M_, M_q, M_c – коэффициенты несущей способности (табл.III.1 приложения III). В формулу (4.21) нужно ввести еще коэффициенты условий работы и надежности.

Для идеально связных грунтов

, (4.22)

. (4.23)

4.4.2. Предельные нагрузки для сыпучих и связных грунтов

Решение дифференциальных уравнений равновесия с учетом условий предельного равновесия позволяет найти математически точные очертания поверхностей скольжения, используя которые, можно оценить значение предельной нагрузки.

Р ис.4.7. Сеть линий скольжения в грунте при полосовой нагрузке

и боковой пригрузке

Впервые эта задача для невесомого грунта, нагруженного полосообразной нагрузкой, была решена Л.Прандтлем и Г.Рейснером (1920-1921):

. (4.24)

Линии скольжения. В треугольнике 0cd имеются два семейства параллельных прямых, наклоненных к горизонту под углом , в пределах угла c0b – пучок прямых, выходящих из точки 0 и сопряженных с ними логарифмических спиралей, и в треугольнике 0ab – два семейства параллельных прямых, наклоненных под углом к горизонту.

Для идеально связных грунтов в случае плоской задачи

, (4.25)

для круга, квадрата

.

При действии наклонной нагрузки с боковой пригрузкой на грунт решение получено В.В.Соколовским

,

где N_, N_q, N_c – коэффициенты несущей способности грунта, табулированные в зависимости от  и  (табл.III.2 приложения III, пример 6). Такая форма уравнения, впервые предложенная проф. К.Терцаги (1943), в настоящее время является канонической и к ней приводятся обычно все другие решения, полученные для предельной нагрузки.

Рис.4.8. Схема действия наклонной

нагрузки на грунт

К.Терцаги получил графики зависимости коэффициентов N от  и принял линии скольжения для невесомого грунта с наличием уплотненного треугольного ядра, грани которого наклонены под углом  к подошве фундамента

, (4.26)

где N' – коэффициенты несущей способности; b₁ – полуширина фундамента.

Рис.4.9. Зоны предельного равновесия под ленточным фундаментом (по Терцаги):

а – схема линий скольжения;

б – кривые коэффициентов несущей способности

Для оснований массивных фундаментов предельную нагрузку следует определять с учетом жесткого ядра ограниченных смещений, формирующегося под подошвой жестких фундаментов, что является сложной задачей, решение которой в замкнутой форме не получено. В этом случае поверхности скольжения задаются, но такие, которые совпадают с точными.

Р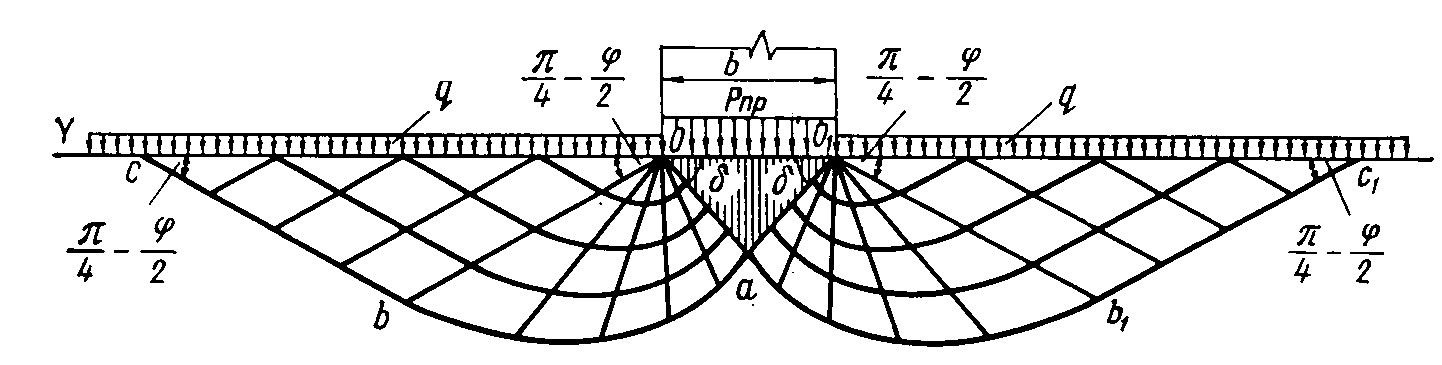 ис.4.10. Сеть линий скольжения в грунте под жестким полосообразным фундаментом с учетом уплотненного ядра

Существуют решения задач для полосообразной нагрузки, круга, квадрата (табл.III.3, III.4 приложения III, пример 7):

. (4.27)

Для фундаментов глубокого заложения h/b  2 нельзя принимать q = h, в этом случае следует принимать для условий плоской задачи

P_nh = A_nb, (4.28)

а для условий пространственной задачи (круглой или квадратной площади)

P_kh = A_kb₁, (4.29)

где A_n и A_k табулированы в зависимости от ширины фундамента и угла внутреннего трения (рис.4.11, 4.12). Сравнение расчетных и фактических данных показало, что фактическая несущая способность, как правило, значительно выше расчетных. Для идеально связных грунтов теоретические данные практически совпадают с экспериментальными.