6. Ряды динамики

Изучив эту тему, студент должен понять, что такое ряды динамики, их элементы, виды рядов динамики, средние показатели рядов динамики, цель и методы выравнивания рядов динамики.

Статистика изучает различные социально-экономические явления в их развитии. Процесс развития общественных явлений во времени называется динамикой.

Статистические ряды динамики – это форма отображения развития явления во времени.

Ряды динамики подразделяются на ряды динамики абсолютных, средних и относительных величин. По признаку времени ряды динамики абсолютных величин подразделяются на моментные и интервальные ряды динамики.

Моментный ряд динамики характеризует состояние явления на определенный момент (дату) времени.

Интервальный ряд динамики характеризует какие-либо итоги за определенный промежуток времени. Интервалами в ряду динамики могут быть различные периоды времени.

Каждый ряд динамики состоит из двух элементов: периодов или моментов времени; уровней ряда.

Уровни ряда динамики должны быть сопоставимы по методологии расчета показателя, территории, продолжительности периодов, охватываемого объекта, единицам измерения и другим признакам.

В тех случаях, когда вначале имеются уровни ряда, исчисленные по одной методологии или в одних границах, а затем уровни, исчисленные по другой методологии или в других границах, уровни ряда динамики оказываются несовместимы между собой. Чтобы привести уровни ряда динамики к сопоставимому, годному для анализа виду, необходимо произвести смыкание рядов динамики.

Пример 1. Имеются данные об объеме транспортной работы (грузообороте) автотранспортных предприятий, обслуживающих регион грузовыми перевозками:

Динамика грузооборота автотранспортных предприятий региона

за 07-11гг. (млн. ткм)

№ п/п	Грузооборот	Год
		07	08	09	10	11
1.	В прежних границах	250	280	–	–	–
2.	В новых границах		380	405	415	438
3.	Сопоставимый ряд	350	380	405	415	438

Два ряда динамики (в прежних и новых границах) привести к сопоставимому виду.

Решение: Определим коэффициент пересчета (коэффициент соотношения двух уровней) в 08 году, в котором произошло изменение границ региона:

К_п = ,

К_п = = 1,4.

Умножая на этот коэффициент уровни ряда динамики в прежних границах, приводим их к сопоставимым уровням в новых границах:

= 350 млн. ткм.

Теперь представим полученные данные о грузообороте (млн. ткм) в виде ряда динамики (см. табл. 7.1.)

07г. 08г. 09г. 10г. 11г.

350 380 405 415 438

Данные сопоставимого ряда характеризуют рост грузооборота в регионе за 07-11 гг., и они могут быть использованы для расчета аналитических показателей динамики.

Для изучения интенсивности изменения уровней ряда во времени исчисляются следующие аналитические показатели динамики: абсолютные приросты, темпы роста, темпы прироста, абсолютные значения одного процента прироста.

Перечисленные показатели динамики можно исчислить с переменной или постоянной базой. Если производится сравнение каждого уровня с предыдущим уровнем, то получаются показатели динамики с переменной базой (цепные показатели динамики). Если каждый уровень сравнивается с начальным уровнем или уровнем, принятым за базу сравнения, то получаются показатели динамики с постоянной базой сравнения (базисные показатели динамики). База сравнения должна выбираться обоснованно, в зависимости от экономических особенностей явления и задач исследования.

Методы расчета аналитических показателей динамики следующие:

1. Абсолютные приросты определяются как разность уровней ряда:

цепные базисные

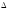y_ц = у_i – y_i-1 y_б = у_i – y_о

Абсолютные приросты показывают, как изменяется изучаемое явление за определенный период времени в именованных числах. Измеряется абсолютный прирост в тех же единицах, что и уровни ряда.

2. Темпы (коэффициенты) роста определяются как отношение уровней ряда:

цепные базисные

k = k =

Измеряются темпы роста либо в коэффициентах, либо в процентах и показывают, во сколько раз уровень рассматриваемого периода больше или меньше уровня предыдущего или базисного периодов.

Если темпы роста выражены в коэффициентах, то всегда можно перейти от цепных темпов к базисным и наоборот, пользуясь двумя правилами:

а) Произведение цепных темпов роста дают базисный темп роста.

б) Частное от деления базисных темпов роста равно промежуточному цепному.

3. Темпы прироста определяются как отношение абсолютного прироста к первоначальному уровню, и выражено в процентах:

цепные базисные

Δk_ц = , Δk_б = ,

или другая методика расчета:

Δk = k % – 100.

Темп прироста показывает, на сколько процентов изменился уровень изучаемого явления за определенный промежуток времени.

4. Абсолютные значения одного процента прироста определяются как отношение абсолютного прироста к темпу прироста:

А % =

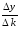
или: первоначальный уровень, деленный на 100:

А % = 0,01 у_i-1.

При расчете показателей приняты следующие условные обозначения:

у_i – уровень ряда рассматриваемого периода;

у_i-1 – уровень ряда предыдущего периода;

у_о – уровень ряда базисного периода.

При анализе развития явлений часто возникает потребность дать обобщенную характеристику интенсивности развития на длительный период. Для чего используют средние показатели динамики: