5.5. Показатели вариации

Информации о средних уровнях исследуемых показателей обычно бывает недостаточно для глубокого анализа изучаемого процесса или явления. Необходимо также учитывать и вариацию значений отдельных единиц относительно средней, которая является важной характеристикой изучаемой совокупности. Значительной вариации, например, подвержены курсы акций, объемы спроса и предложения, процентные ставки в разные периоды.

Основными показателями, характеризующими вариацию, являются размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Для иллюстрации расчетов этих показателей воспользуемся следующими данными

Таблица Страховые выплаты за год по договорам страхования от несчастных случаев

Сумма выплат, тыс. руб.	Число выплат
5	11
6	17
7	23
8	30
9	18

Простейшим показателем при группировке данных является размах вариации. Он представляет собой разность максимального и минимального значений признака:

R=X_max – X_min= 9 - 5 = 4 тыс.руб.

Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ. Этого недостатка лишена дисперсия, рассчитываемая как средний квадрат отклонений значений признака от их средней величины. Как и средняя величина, дисперсия может рассчитываться по невзвешенной или по взвешенной формуле. Взвешенная формула используется в тех случаях, когда варианты значений изучаемого признака повторяются:

невзвешенная формула:

взвешенная формула:

По данным табл. определим средневзвешенный размер страховой выплаты и рассчитаем дисперсию:

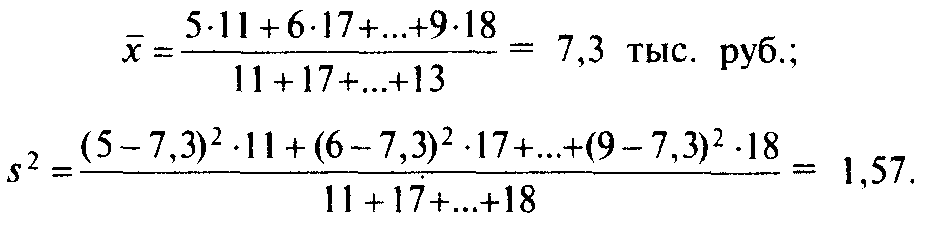
Дисперсию в отдельных случаях удобнее рассчитывать по другой формуле, представляющей собой алгебраическое преобразование приведенных выше выражений:

где илих²=

Другим наиболее широко распространенным на практике показателем является среднее квадратическое отклонение. Оно определяется как квадратный корень из дисперсии и имеет ту же размеренность, что и изучаемый признак:

В нашем случае получим:

 = (1,57)^0,5= 1,25 тыс. руб.

Рассмотренная величина показывает, что произведенные страховые выплаты отклонялись от их средневзвешенного размера в среднем на 1,25 тыс. руб.

Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. В отличие от них коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня, что во многих случаях является более предпочтительным:

Определим значение этого показателя по нашим данным:

Рассчитанная величина свидетельствует о сравнительно низком относительном уровне колеблемости страховых выплат. Если Vне превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной.

Показатели вариации также являются составной частью или основой для расчетов других статистических показателей. Они используются в анализе взаимосвязей между признаками, в измерении структурных сдвигов в экономике, в оценке рисков (страхового, систематического на рынке ценных бумаг и проч.).