Средняя ошибки для генеральной доли при бесповторном способе отбора;

μ =

средняя ошибки для выборочной доли при бесповторном способе отбора.

В практике бывает необходимо определить не только величину ошибки, но и пределы, за которые она не должна выходить.

Пределы, за которые не выйдет величина конкретной ошибки выборочного наблюдения, можно установить не с абсолютной достоверностью, а лишь с определенной степенью вероятности.

Доказано, что генеральные характеристики не отклоняются от выборочных

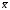=μ

p = w μ

на величину большую, чем величина ошибки выборочного наблюдения (μ), и всегда имеют равную вероятность 0,683. Т.е. можно утверждать, что из 1000 случаев в 683 случаях выборочная средняя или выборочная доля будут отличаться от генеральной средней или генеральной доли на величину средней ошибки выборочного наблюдения (μ), а в 317 случаях может отличаться больше, чем на 1μ.

Может быть:

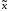
=2μ

p = w2μ

В этом случае степень вероятности повышается до 0,954.

При=3μ

p = w3μ

степень вероятности повышается до 0,997.

Ошибка выборочного наблюдения, исчисленная с заданной степенью вероятности, называется предельной ошибкой выборки ():

Δ=,

где t – коэффициент доверия.

Следовательно, величина предельной ошибки выборочного наблюдения зависит от величины средней ошибки и коэффициента доверия, а коэффициент доверия в свою очередь зависит от степени вероятности, с которой проводится выборочное наблюдение.

В зависимости от принятой вероятности определяется значение коэффициента доверия (или кратности) (t) по удвоенной нормированной функции Лапласа:

Ф(t) = ,

где Ф(t) – интеграл Лапласа (берется по таблицам нормального распределения).

Формулы предельной ошибки выборочного наблюдения можно записать так:

• для количественно изменяющегося признака при бесповторном способе отбора

Δ_х = t ;

• для качественно изменяющегося признака при бесповторном способе отбора

Δ_w = t .

Определение пределов генеральных характеристик с заданной степенью вероятности на основе показателей, полученных по данным выборки, можно выразить следующим образом:

• доверительные интервалы для средней

=Δ_х

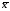
–Δ_х + Δ_х ;

• доверительные интервалы для генеральной доли

p = w Δ_w

w – Δ_w p w + Δ_w.

Пример 1. Для определения качества партии товара 3% от всего количества изделий были подвергнуты выборочному обследованию. Из 800 проверенных изделий 200 были нестандартными. Определить с вероятностью 0,954 долю нестандартных изделий во всей партии.

Решение: По условию задачи дано:

= 3% или 0,03

n = 800 изд. Определим долю нестандартных изделий в

m = 200 изд. выборочной совокупности:

t = 2 w = 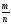== 0,25 или 25%.

Из 800 проверенных изделий 25% – нестандартные

w – ? Δ_w – ? изделия.

Определим предельную ошибку выборочного наблюдения:

Δ_w = t

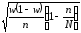
или Δ_w = 2 = 0,03 или 3,0%.

Доверительные интервалы для доли будут равны:

p = w Δ_w

p = 25% 3%, тогда 25% – 3%p 25% + 3%.

Доля нестандартных изделий во всей партии будет находиться в пределах от 22 до 28% при вероятности 0,954.

Пример 2. Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 10%-ная механическая выборка, в которую попало 200 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении 9 дней. С вероятностью 0,997 определить пределы, в которых будет находиться средний срок пользования краткосрочным кредитом в генеральной совокупности.

Решение. Средний срок пользования кредитом в банке находится в пределах:

–Δ_х + Δ_х .

Так как выборка механическая, то ошибка выборочного наблюдения определяется по формуле:

Δ_х = t ;

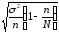Δ_х = 3 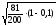= 1,812 дня

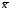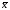
=30 дн.2 дн. или 30 дн.–2 дн.30 дн.+2 дн.

С вероятностью 0,997 можно утверждать, что средний срок пользования краткосрочным кредитом в банке находится в пределах от 28 дней до 32 дней.

Для определения необходимой численности выборки исследователь должен задать уровень точности выборочной совокупности с определенной вероятностью. Численность случайной повторной выборки определяется по формуле:

,

бесповторной:

.

_отн = _x /x , или _отн = _w /w, v =  /x.

Если расчет проводится по качественному альтернативному признаку и не известна его доля в генеральной совокупности, её принимают равной 0,5, так как дисперсия доли достигает максимума: = 0,25 приw = 0,5.

.