
Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ
.pdf
Численные методы решения задач линейной алгебры
(m1d11 - l) y1 + m2d12 y2 + ... + mn d1n yn = 0, ü
m1d21 y1 + (m2d22 - l) y2 + ... + mnd2n yn = 0,ïï
ý
LLLLLLLLLLLLLLLLLL ï m1dn1 y1 + m2dn2 y2 + ... + (mn dnn - l)yn = 0,ïþ
а соответственно и определитель вида:
|
(m1d11 - l) |
m2d12 |
L mnd1n |
|
|
|
|
||||
|
m1d21 |
(m2d22 - l) L mnd2n |
= 0 , |
||
|
M |
M |
M |
M |
|
|
|
||||
|
m1dn1 |
m2dn2 |
L (mndnn - l) |
|
|
(2.58)
(2.58а)
где mi – сосредоточенные массы; yi – отклонения масс;
δij – перемещения масс, определяемые по единичным эпюрам;
λ = ω12 , (w – частота собственных колебаний системы).
При решении задачи устойчивости упругой системы с конечным числом степеней свободы (n), система уравнений равновесия, описывающая деформированное состояние конструкции, обычно приводится к виду (2.57), где l – величина, зависящая от параметра критических сил Рi. А определитель, из которого находят значения критических нагрузок Рi,, имеет вид (2.57а). Практическое значение в задачах устойчивости обычно имеет только первая (наименьшая) критическая нагрузка Pmin.
Если определитель (2.57а) раскрыть, то получится полином степени n относительно l:
ln - р1ln−1 + р2ln−2 -...рn−1l + (-1)n рn = 0 . |
(2.59) |
83

Численные методы решения задач линейной алгебры
Все корни этого уравнения положительны и каждому из них при решении задач динамики соответствует свое значение
частоты: ω1 = 
 1λ1 , ω2 =
1λ1 , ω2 = 
 1λ2 ,…, ωn =
1λ2 ,…, ωn = 
 1λn .
1λn .
Число частот равно числу степеней свободы системы.
Совокупность этих величин называют спектром частот. Каждой частоте соответствует своя форма колебаний.
В задачах устойчивости каждому корню уравнения (2.59) соответствует свое значение критической нагрузки Рi.
Подставляя в систему (2.57) поочередно собственные значения λ1, λ2,..., λn, найдем все координаты собственного вектора X .
В задачах о колебаниях систем координаты собственного вектора – это амплитуды свободных колебаний,
соответствующие колебаниям с различными частотами ω, а в
задачах устойчивости – формы потери устойчивости,
соответствующие разным критическим нагрузкам Р.
При определении собственных значений и собственных векторов матриц решается одна из двух задач:
1)определение всех собственных значений и принадлежащих им собственных векторов матриц – полная проблема
собственных значений
или
2)определение одного или нескольких собственных значений и
принадлежащих им собственных векторов – частичные проблемы собственных значений.
Первая задача состоит в развертывании характеристического определителя в многочлен n-й степени (то есть в определении коэффициентов р1, р2,..., р n) с последующим приближенным вычислением собственных значений λ1,λ2,,..., λn, и, наконец, в
определении координат собственного вектора X = (x1 , x2 ,K, xn ) .
84

Численные методы решения задач линейной алгебры
Методы решения этой задачи называют точными и применяют, в основном, при нахождении корней характеристических многочленов для матриц невысоких порядков.
Вторая задача заключается в приближенном определении корней характеристического уравнения λi (чаще всего наибольшего или наименьшего по модулю) методом итерации, без предварительного развертывания векового определителя. Методы решения данной задачи являются итерационными. Здесь
собственные значения получаются как пределы некоторых числовых последовательностей так же, как и координаты принадлежащих им собственных векторов.
Рассмотрим методы нахождения собственных значений и собственных векторов числовой матрицы на примерах некоторых частных задач, имеющих практическое приложение в строительстве.
2.8.2. Методы развертывания вековых определителей
Если требуется найти все корни характеристического уравнения, то определитель det (A −λE) следует развернуть в полином n-й степени (2.59). Для определителей 2-го и 3-го порядка это не составляет особого труда. Если же требуется развернуть определитель более высокого порядка в многочлен n-й степени, то коэффициенты р1, р2,..., р n можно вычислить по следующим формулам:
n
р1 = åаii = SpA – сумма всех диагональных элементов
i=1
матрицы А (след матрицы),
p2 = å |
aαα |
aαβ |
– сумма всех диагональных миноров |
|
a |
βα |
a |
||
α<β |
|
ββ |
|
|
второго порядка матрицы А,
85
Численные методы решения задач линейной алгебры
p3 = å |
aαα |
aαβ |
aαγ |
|
aβα |
aββ |
aβγ |
– сумма всех диагональных миноров |
|
α<β<γ |
aγα |
aγβ |
aγγ |
|
третьего порядка матрицы А.
………………………………………………………………………….
pn = det A – определитель матрицы А.
Число диагональных миноров k-го порядка матрицы А
Cnk = |
n(n −1)(n − 2)...(n − k +1) |
(k=1, 2, …n). |
|
k! |
|||
|
|
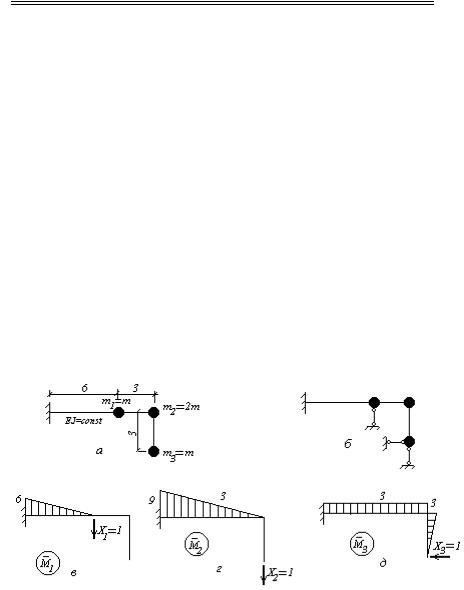
n Пример 2.11. Найдем частоты собственных колебаний системы с тремя степенями свободы, показанной на рис. 2.3,а, при т1=т3=т и т2=2т. На рис 2.3,б показаны введенные связи, по направлению которых будут ориентированы силы инерции. Движение масс из плоскости чертежа считаем невозможным. Вращением масс пренебрегаем. Эпюры от единичных сил инерции Х1=1, Х2=1, Х3=1 приведены на рис. 2.3, в, г, д. При определении перемещений учитываем только изгибные деформации.
Рис.2.3. К примеру 2.11
86

Численные методы решения задач линейной алгебры По единичным эпюрам находим:
δ11 |
= |
6×6 2 |
6 = |
|
72 |
; |
|
δ 22 = |
9×9 2 |
9 = |
243 |
|
; |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2EJ 3 |
EJ |
2EJ 3 |
EJ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
δ 33 |
= |
3×3 2 |
3+ |
|
9×3 |
3 = |
|
90 |
; |
δ12 |
= δ 21 = |
6×6 |
(3+ |
|
2 |
6) = |
126 |
; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2EJ 3 |
EJ |
EJ |
2EJ |
3 |
|
EJ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
δ13 |
= δ31 = |
6×6 |
|
3 = |
54 |
|
; |
|
δ 23 |
= δ 32 = |
|
9×9 |
|
3 = |
121,5 |
. |
|
|
|
|||||||||
2EJ |
EJ |
|
|
2EJ |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
||||||||
Определение частот свободных колебаний сводится к решению системы однородных уравнений, которая в матричной форме имеет вид
(А - λЕ)у = 0 .
Характеристическое уравнение для данной системы запишется:
é(т1δ11 - λ) |
т2δ12 |
т3δ13 |
ù |
|
|
||||||||||
ê |
т δ |
21 |
(т |
δ |
22 |
- λ) |
т |
|
δ |
23 |
ú |
= 0 . |
(2.60) |
||
ê |
1 |
2 |
|
|
|
3 |
|
ú |
|
|
|||||
ê |
т δ |
31 |
т |
|
δ |
32 |
(т |
δ |
33 |
- λ)ú |
|
|
|||
ë |
1 |
|
2 |
|
3 |
|
|
û |
|
|
|||||
Раскрывая определитель, подставляя найденные значения перемещений и учитывая, что т1=т3=т и т2=2т, будем иметь
кубическое уравнение
é |
|
m |
|
- λ) |
||||||
ê(72 |
|
|
|
|
||||||
EJ |
||||||||||
m ê |
|
m |
||||||||
|
|
|
|
|
||||||
|
ê |
126 |
|
|
|
|
|
|
||
|
|
|
EJ |
|||||||
EJ ê |
|
|
|
|
||||||
ê |
54 |
|
|
m |
||||||
ê |
|
|
|
|
|
|
||||
EJ |
||||||||||
ë |
|
|
||||||||
252 |
|
m |
54 |
|
m |
ù |
|
|||||||
|
|
|
|
|
|
|
|
|
ú |
|
||||
EJ |
EJ |
|
||||||||||||
|
|
|
|
|
ú |
|
||||||||
|
m |
|
|
|
|
|
m |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
(486 EJ - λ) |
121,5 EJ |
ú |
= |
|||||||||||
|
|
|
m |
|
m |
|
|
|
|
ú |
(2.61) |
|||
243 |
|
|
|
|
(90 |
|
|
|
|
- λ)ú |
|
|||
|
EJ |
EJ |
|
|
||||||||||
|
|
|
|
|
|
|
û |
|
||||||
3 |
m |
|
2 |
æ |
m ö2 |
æ |
m ö3 |
|||
= -λ + 648 |
|
λ |
|
- 21019,5ç |
|
÷ |
λ + 55404ç |
|
÷ |
= 0. |
EJ |
|
|
|
|||||||
|
|
|
è |
EJ ø |
è |
EJ ø |
|
|||
Решая данное кубическое уравнение, найдем три корня:
λ = 614 |
m |
; |
λ |
2 |
= 31,2 |
m |
; |
λ |
3 |
= 2,8926 |
m |
. |
|
|
|
||||||||||
1 |
EJ |
|
|
|
EJ |
|
|
|
EJ |
|||
|
|
|
|
|
|
|
|
|
||||
Теперь найдем частоты собственных колебаний:
87

|
Численные методы решения задач линейной алгебры |
||||||||||||
ω1 = 1 |
|
= 0,04 |
|
|
; |
|
ω2 = 1 |
|
= 0,179 |
|
|
; |
|
λ1 |
(EJ) m |
λ2 |
(EJ ) |
m |
|||||||||
ω3 =1 |
|
|
= 0,588 |
|
|
. |
|
|
|
|
|
|
|
λ3 |
|
(EJ ) m |
|
|
|
|
|
|
|||||
Таким |
образом, |
|
наименьшей |
частоте |
колебаний |
соответствует |
|||||||
наибольшее значение l.
Непосредственное вычисление коэффициентов характеристического полинома (2.59) эквивалентно вычислению определителей различных порядков. Задача эта, вообще говоря, технически трудно осуществима для больших значений n. Поэтому
созданы специальные методы развертывания вековых определителей (методы А.Н.Крылова, А.М.Данилевского, Леверрье и др.[12]). Но в большинстве практических задач бывает достаточно определить только одну наименьшую частоту, поэтому
при решении характеристического уравнения ставится задача найти только одно характеристическое число λmax.
2.8.3. Итерационные методы определения максимального по модулю собственного значения матрицы
С помощью итерационных методов можно определить максимальное по модулю собственное число матрицы А без раскрытия характеристического определителя. Существуют разные варианты итерационного процесса [12] для нахождения наибольшего по модулю собственного значения λ1 матрицы А. Все
они с разной скоростью позволяют получить решение требуемой точности. Рассмотрим один из таких методов.
Пусть det(A − λE) = 0 – характеристическое уравнение. λ1,
λ2,,..., λn, – его корни, являющиеся собственными значениями матрицы А.
Предположим, что λ1 > λ2 ³ λ3 ³ ... ³ λn ,
где λ1 – наибольшее по модулю собственное число.
88

Численные методы решения задач линейной алгебры
Тогда для нахождения приближенного значения корня используется следующая схема:
1)выбирают произвольно начальный вектор Х,
2)составляют последовательные итерации:
Х(1)=АХ, Х(2) =ААХ=А2Х,
Х(3)=АА2Х=А3Х,
…………………..
Х(т) =ААт-1Х=АтХ, Х(т+1) =ААтХ=А т+1Х,
3) выбирают из последовательности два последних значения
Х(т) = АтХ |
и |
|
Х(т+1) = А т+1Х. |
|
x(m+1) |
|
|
||
|
λ = lim |
x(m+1) |
|
λ ≈ |
|
|
|||
Тогда |
i |
или |
i |
, |
(2.62) |
||||
|
|
||||||||
|
|
1 |
m→∞ |
x(m) |
|
1 |
x(m) |
|
|
|
|
|
|
i |
|
|
i |
|
|
где x(m+1) и x(m) |
– соответствующие координаты векторов Х(т+1) и |
||||||||
i |
i |
|
|
|
|
|
|
|
|
Х(т) (i=1,2,…,n).
Таким образом, взяв достаточно большой номер итерации т, можно с любой степенью точности вычислить наибольший по модулю корень λ1 характеристического уравнения матрицы. Для
нахождения этого корня может быть использована любая координата вектора Х(т), в частности, можно взять среднее
арифметическое соответствующих отношений для разных координат.
Скорость сходимости этого процесса зависит от выбора начального вектора Х. При неудачном выборе формула (2.62) может не дать нужного корня или даже вообще не иметь смысла,
т.е. предел отношения xi(m+1)  xi(m) может не существовать.
xi(m) может не существовать.
Последнее легко заметить по «прыгающим» значениям этого отношения. В таких случаях следует изменить начальный вектор.
В качестве первого собственного значения можно взять Х(т+1). В задачах на собственные колебания вектор Х выбирается исходя из предположения о моде колебаний, в основе которого
89

Численные методы решения задач линейной алгебры
лежат предположения о физическом явлении или знание результатов модельных испытаний.
nПример 2.12. Найти минимальную частоту собственных колебаний системы с тремя степенями свободы, рассмотренной в примере 2.11.
Определение частот свободных колебаний сводится к решению системы однородных уравнений, которую в матричной форме можно записать:
Ау = λ у . |
(2.63) |
Применим метод последовательных приближений, описанный выше.
Введем обозначение ρ = EJm λ , тогда с учетом того, что т1=т3=т
и т2=2т, вместо (2.63) получим
|
А1 у = ρ у , |
|
|
|
|
|
|
|
|
(2.64) |
||||
é 72 |
252 |
|
54 ù |
|
|
|
|
|
|
|
|
|||
ê |
|
|
486 |
|
|
ú |
|
|
|
|
|
|
|
|
где А1 = ê126 |
121,5ú . |
|
|
|
|
|
|
|
|
|||||
ê |
54 |
243 |
|
90 |
ú |
|
|
|
|
|
|
|
|
|
ë |
|
û |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
é0,5ù |
|
|
|
|
|
|
|
|
|
Зададимся начальным значением у0 |
|
ê |
ú |
. Подставив |
у0 в левую часть |
|||||||||
= ê 1 |
ú |
|||||||||||||
|
|
|
|
|
ê0,5ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
û |
|
|
|
|
|
|
|
|
|
é 72 |
252 |
54 |
ù |
é0,5ù |
é315ù |
é0,517ù |
|||||||
уравнения (2.64), получим: |
ê |
|
486 |
|
|
ú |
ê |
ú |
ê |
ú |
ê |
1 |
ú |
|
ê126 |
121,5ú × ê 1 |
ú |
= ê609ú |
= 609ê |
ú . |
|||||||||
|
ê |
54 |
243 |
90 |
ú |
ê0,5ú |
ê315ú |
ê0,517ú |
||||||
|
ë |
|
|
|
|
|
û |
ë |
û |
ë |
û |
ë |
|
û |
|
|
|
|
|
é0,517ù |
|
|
|
|
|
|
|||
В первом приближении ρmax |
= 609 , |
|
ê |
1 |
ú |
|
|
|
|
|
|
|||
y1 = ê |
ú . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
ê |
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
ë0,517û |
|
|
|
|
|
|
|||
90
Численные методы решения задач линейной алгебры
|
|
é0,5166ù |
|
||
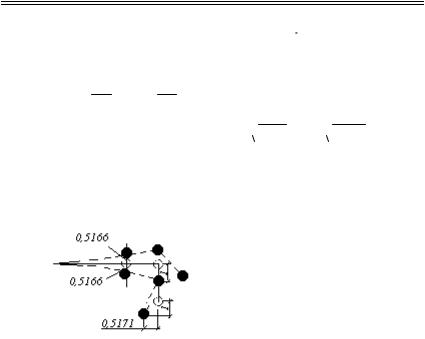
Проделав три итерации, получим ρmax = 614 , |
y |
ê |
1 |
ú |
; |
3 = ê |
ú |
||||
|
|
ê |
0,5171ú |
|
|
|
|
ë |
|
û |
|
λmax = mEJρ = 0,614 EJm , что совпало с решением в примере 2.11.
Минимальная частота колебаний: ωmin = 1

 λmax = 0,04
λmax = 0,04
 EJ
EJ m .
m .
Отложив по направлениям Х1, Х2 и Х3 ординаты собственного вектора, получим соответствующие перемещения масс и форму изгиба стержней, показанные на рис.2.4.
Рис.2.4. Перемещения масс
и форма изгиба стержней при минимальной частоте колебаний системы
2.9.Примеры решения задач линейной алгебры
сиспользованием электронных таблиц Microsoft Excel
2.9.1. Реализация метода Гаусса средствами приложения Excel
Рассмотрим решение системы линейных алгебраических уравнений (пример 2.1) методом Гаусса, используя таблицы Excel.
2x1 |
+ 4x2 |
+ 3x3 = 4, ü |
|
|
3x1 |
+ x2 - 2x3 = -2, |
ï |
(2.65) |
|
ý |
||||
4x1 +11x |
|
ï |
|
|
2 + 7x3 = 7.þ |
|
|||
Последовательность действий
Введем расширенную матрицу системы, как показано на рис.2.5, в ячейки А3:D5.
91

Численные методы решения задач линейной алгебры
Рис.2.5 Реализация метода Гаусса в MS Excel
Первый этап (прямой ход метода Гаусса).
Поделим элементы первой строки на а11 .Для этого в ячейку А7 введем формулу «=А3/A$3$». Далее аналогичные действия
будем записывть в виде
А7=А3/A$3$*
и скопируем ее вправо до конца строки.
Умножим элементы первой строки на (–а21 ) и прибавим ко
2-й строке. Для этого введем формулу А8=А7(-А$4$)+А4
и скопируем ее вправо до конца строки.
Умножим элементы первой строки на (–а31 ) и прибавим к
3-й строке. Для этого введем формулу А9=А7(-А$5$)+А5
и скопируем ее вправо до конца строки.
Таким образом исключили неизвестное х1 из 2-го и 3-го уравнений системы (смотри 1-й шаг рис.2.5).
* - данная запись означает, что в ячейку А7 вводится формула, начинающаяся со знака «=» (равно).
92
