Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ

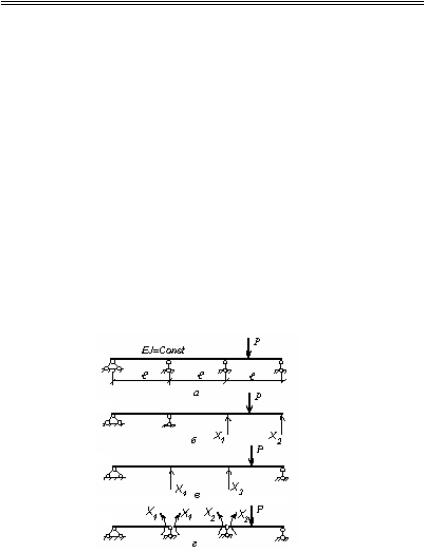
Численные методы решения задач линейной алгебры

A = max {8, 12, 11, 11}=12; A−1 = max {0,291; 0,258; 0,292; 0,249}=0,292;

m(A)=12´0,292=4,506, то есть m(A) невелика и матрица А хорошо обусловлена,

B = max {21,21,21,1}=21; B −1 = max {8421, 421, 21, 1}=8421

m(B) =21´8421=176841, то есть величина m(B) очень большая и матрица В плохо обусловлена.

nПример 2.9. Рассмотрим три варианта основной системы метода сил для трехпролетной неразрезной балки (рис.2.1).

Рис.2.1. Основные системы для неразрезной балки

В методе сил важным критерием оценки выбранной основной системы является обусловленность коэффициентов системы канонических уравнений. Запишем матрицы податливости и значения меры обусловленности для этих вариантов (табл. 2.1).

73

Численные методы решения задач линейной алгебры

Таблица 2.1

Из сравнения величин меры обусловленности m ясно, что вариант основной системы г) является лучшим, а вариант б) – худшим из трех.

2.6. Вычисление определителя

Как уже говорилось выше, вычислительные затраты на

вычисление определителя соизмеримы с затратами на решение системы линейных алгебраических уравнений.

На примере вычисления определителя можно убедиться в экономичности хороших численных методов.

Вспомним формальное определение определителя, как

суммы всевозможных произведений элементов, взятых из разных строк и столбцов. Таких произведений n! И прямое их вычисление уже при небольшом n ≈30 требует астрономического числа действий > 1030, что вряд ли под силу ЭВМ. А метод исключения Гаусса, например, легко позволяет вычислить определитель сотого и более порядка. В самом деле, в процессе прямого хода, приводя матрицу к треугольному виду и получая эквивалентную матрицу,

мы для этой матрицы получим нулевые значения всех произведений элементов, кроме диагональных. То есть величина

определителя треугольной матрицы равна произведению всех диагональных элементов:

i=1

74

Численные методы решения задач линейной алгебры

При этом мы производим следующие операции:

1)деление строки матрицы на ведущий элемент (который предполагается отличным от нуля), что уменьшает величину определителя в такое же число раз, следовательно, вычисляя определитель, надо домножить его на это число;

2)умножение строки матрицы на число и сложение ее с другой строкой, что не влияет на величину определителя;

3)знак определителя может измениться, если производилась

перестановка строк.

Таким образом, величина определителя может быть

вычислена по формуле

det A = ±a11(1) ×a22(2) Kann(n) ,

то есть, определитель равен произведению ведущих элементов для соответствующей схемы Гаусса. Знак ± зависит от того, четной или нечетной была суммарная перестановка строк.

n Пример 2.8. Для матрицы А вычислить определитель методом Гаусса.

В практических задачах редко возникает необходимость в явном виде вычислять значение определителя. Однако иногда они оказываются весьма полезны, например, при исследовании

геометрической неизменяемости сооружений. В курсе

строительной механики рассматриваются геометрические принципы образования неизменяемых систем, которые удается

75

Численные методы решения задач линейной алгебры

применить далеко не для всех конструкций (см. пример 2.9.). В таких случаях следует использовать аналитическое решение,

записав определяющую систему уравнений:

–для статически определимых систем – уравнения равновесия,

–для статически неопределимых –- канонические уравнения какого-либо метода.

Если Det A → 0, система стремится к мгновенно изменяемой,

при Det A=0 система геометрически изменяема. Достаточным

условием геометрической неизменяемости системы является выполнение неравенства Det A ¹ 0.

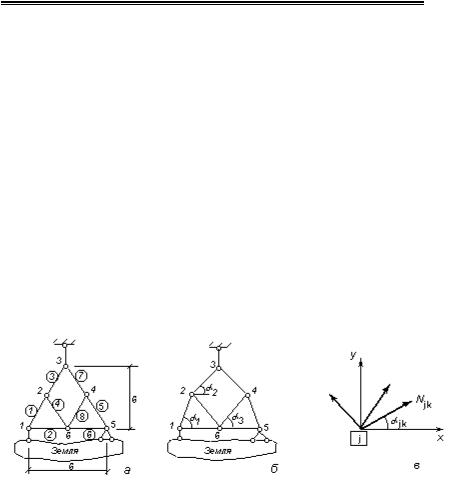
n Пример 2.9. Стержневые системы, изображенные на рис.2.2, статически определимы, имеют одинаковое число стержней и узлов. Число связей достаточно, чтобы они были геометрически неизменяемыми (2У–С–Соп= 2*6–8–4=0). По внешнему виду системы мало отличаются одна от другой. Но первая является геометрически изменяемой а вторая –-

неизменяемой системой.

Рис. 2.2. К примеру 2.9

Установить это с помощью известных геометрических принципов образования систем вряд ли удастся. В подобных случаях приходится применять аналитическое решение.

Составляя уравнения равновесия узлов в виде проекций сил на оси Х и У при нулевой нагрузке в виде

76

Численные методы решения задач линейной алгебры

где суммы содержат столько слагаемых, сколько стержней примыкает к рассматриваемому j-му узлу, получим следующую однородную систему линейных алгебраических уравнений:

AN = 0 ,

которая в случае Det A ¹ 0 должна иметь только нулевое решение, т.е. при нулевой нагрузке все усилия в стержнях фермы должны равняться нулю.

Здесь N – вектор неизвестных усилий в стержнях системы (включая опорные стержни), а элементами матрицы А являются синусы и косинусы углов наклона стержней к оси Х (рис.2.2,в).

Вид матрицы А зависит от нумерации узлов и стержней, но если ферма геометрически неизменяема, то определитель отличен от нуля при любой нумерации.

Для вариантов, показанных на рис.2.2, определитель матрицы А

имеет вид

77

Численные методы решения задач линейной алгебры

Номер столбца соответствует номеру стержня. Для каждого узла составлено по два уравнения равновесия, т.е. занято по две строки. С учетом того, что:

определитель матрицы А для системы а) получается равным нулю, а для б) detA=0,192– отличен от нуля. Следовательно, первая стержневая система является геометрически изменяемой, а вторая – геометрически неизменяемой системой.

2.7. Вычисление обратной матрицы

Пусть дана неособенная матрица А=[aij] (i,j=1,2,..., n). Для

нахождения ее обратной матрицы используем основное соотношение:

где Е –- единичная матрица.

Обозначим элементы обратной матрицы αij . Тогда это

соотношение можно записать

Каждый столбец обратной матрицы можно считать вектором неизвестных

78

Численные методы решения задач линейной алгебры

и для того, чтобы найти все элементы обратной матрицы, надо решить n систем линейных алгебраических уравнений, с одной и

той же матрицей коэффициентов А и разными векторами правой

части B j , содержащими одну единицу (при i=j), а остальные нули.

Следует отметить, что при решении этих n систем, например,

методом Гаусса, приведение матрицы А к треугольному виду делается только один раз. Поэтому обращение матрицы этим методом требует лишь в три раза больше действий, чем решение одной системы уравнений (обратный ход выполняется намного быстрее, чем прямой).

n Пример 2.10 Методом Гаусса найти обратную матрицу А -1 для

матрицы

Для нахождения элементов αij надо решить 3 системы линейных

é1 1 2ù

алгебраических уравнений с одинаковой матрицей А= êê3 4 1úú :

êë0 1 2úû

79

Численные методы решения задач линейной алгебры

Приводя матрицу коэффициентов к треугольному виду и выполняя обратный ход для каждой системы, получаем:

2.8. Нахождение собственных значений и собственных векторов матриц

Собственные векторы и собственные значения являются характеристиками матрицы и играют большую роль в решении технических задач, в частности, задач динамики и устойчивости зданий и сооружений [12].

2.8.1. Вводные замечания

Пусть А = [aij] – квадратная матрица n-го порядка с действительными элементами и λ – некоторое неизвестное. Тогда матрица А–λЕ называется характеристической матрицей матрицы

А (здесь Е – единичная матрица):

80

Численные методы решения задач линейной алгебры

Определитель этой матрицы называется

характеристическим определителем и равен

В развернутом виде det (A −λE) есть многочлен (полином) n-й степени от λ :

называемый характеристическим многочленом матрицы А. Числа

р1,р2,..., р n называются коэффициентами характеристического многочлена. λ1, λ2,..., λn, называются характеристическими числами или собственными значениями матрицы А.

Ненулевой вектор X = (x1, x2 ,K, xn ) называется собственным

вектором матрицы А, если эта матрица переводит вектор X в

вектор

Таким образом, каждому собственному значению λi матрицы соответствует свой собственный вектор Xi (i=1,2,...,n).

Для определения координат собственного вектора составим уравнение

81

Численные методы решения задач линейной алгебры

Переписав его в виде

и выполнив умножение, получим систему линейных однородных

уравнений

Данная система имеет нетривиальное (ненулевое) решение только в том случае, когда определитель, составленный из коэффициентов при неизвестных х1, х2,…, хn, равен нулю, т.е.

Уравнение (2.57a) называется характеристическим (частотным –

в теории колебаний) или вековым (это название возникло в связи с

задачами небесной механики о периодических отклонениях планет от своих орбит). Искомой величиной в нем является собственное значение l.

При решении задач о собственных колебаниях системы с n

степенями свободы обычно получается система

82