Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ

Матричное исчисление

Расчет статически неопределимых систем в

строительной механике обычно производится с помощью

классических методов строительной механики: метода сил и метода перемещений.

Расчет систем любым из этих методов в матричной форме производится в два этапа:

первый этап включает в себя выбор основной системы и составление исходных матриц, описывающих упругие свойства системы, ее геометрию и условия внешнего воздействия;

второй этап расчета состоит в последовательности матричных операций, которая одинакова для всех задач, решаемых одним и тем же методом.

1.5.3. Матричная форма метода сил

Пусть задана стержневая система, имеющая n лишних связей. Требуется рассчитать эту систему методом сил на t различных видов загружения.

Система канонических уравнений метода сил в матричной форме запишется в виде

33

Матричное исчисление

1.5.4. Матричная форма метода перемещений

При расчете системы, степень кинематической неопределимости которой равна n на t видов загружений,

канонические уравнения метода перемещений в матричной форме имеют вид

− или матрица единичных реакций во введенных связях основной системы метода перемещений.

34

Матричное исчисление

1.5.5. Связь между матрицей податливости и матрицей жесткости

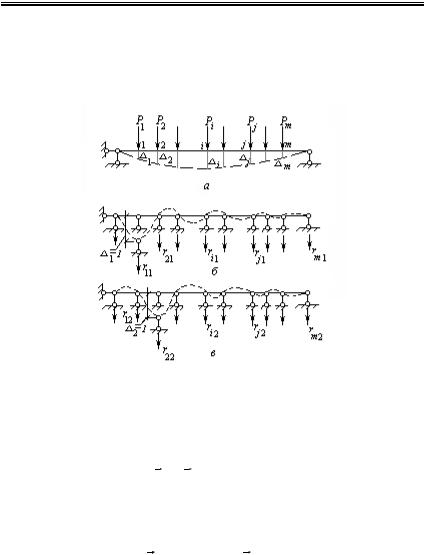
Рассмотрим какую-либо деформируемую систему и приложим к ней систему сил Р1, Р2, …,Рm (рис. 1.5, а).

Рис.1.5. Деформируемая балка

Возникающие при этом перемещения 1, 2,…, т

определяются на основании обобщенного закона Гука

где δ – матрица единичных перемещений;

Потребуем, чтобы все перемещения, кроме 1, равнялись нулю

(рис. 1.5,б):

35

Матричное исчисление

é1ù ê0ú D1 = êêêMúúú

ë0û

и будем разыскивать соответствующий вектор нагрузок

P = δ−1 D1 .

Эту задачу можно трактовать как нахождение реакций в т связях при смещении одной из них на единицу (рис. 1.5,б ).

Тогда из первого уравнения, получим

r1 = δ−1 D1 .

Затем сместим на единицу вторую связь (рис. 1.5,в) и найдем так

же

r2 = δ−1 D2 .

36

Матричное исчисление

где

т.е. матрица жесткости и матрица податливости взаимно

обратны.

1.6. Матрицы в расчетах инженерных сетей

Матричная форма расчета является удобной и при расчете инженерных сетей. Для иллюстрации рассмотрим гидравлическую сеть, изображенную на рис. 1.6.

Рис. 1.6. Гидравлическая сеть

37

Матричное исчисление

В случае медленных (ламинарных) течений поток Q через

поперечное сечение трубы пропорционален разности давлений в начале и конце трубы. Таким образом, для элемента е6 (рис. 1.7) потоки в эту трубу в узлах 2 и 3 соответственно будут

Q2 и Q3 – потоки в тех же узлах,

с – постоянная, зависящая от свойств жидкости, диаметра и длины трубы.

Рис. 1.7. Элемент (труба) е6

В матричной форме уравнения (1.32) можно записать

Уравнение (1.32 б) – это матричное уравнение для элемента e6. Оно также может быть записано в виде расширенного матричного уравнения, включающего все узлы сети:

38

Предположим, что жидкость поступает в сеть в узлах 1, 2, …, 8 с расходами R1, R2 ,…, R8 соответственно. Уравнение неразрывности для узла 2, например, имеет вид

Система уравнений типа (1.33) может быть записана следующим образом:

Подстановка уравнений типа (1.32 г) в (1.34) приводит к

матричному уравнению системы

Для заданных подводимых потоков узловые давления могут быть найдены путем решения уравнения (1.35). После этого расходы

39

Матричное исчисление

через каждую трубу можно вычислить с помощью уравнений типа

(1.32).

nПример 1.6. Пусть сеть труб, показанная на рис. 1.6, является частью системы водоснабжения поселка. Из-за повреждения дамбы давление в системе мало и поток в трубах считается ламинарным. Основываясь на этом, вычислим вытекающие потоки в узлах 6, 7 и 8 для следующих данных:

Перепад давления D р для ламинарного потока в трубе диаметром d и длиной l вычисляется по уравнению Гагена – Пуазейля

где m – динамическая вязкость и v – средняя скорость, с использованием согласованной системы физических единиц.

Предполагается, что вода в системе имеет постоянную температуру

16°С, динамическая вязкость равна 1,1×10-4 кг·с/м2, все трубы горизонтальны и утечка в стыках пренебрежимо мала.

Из эксперимента известно, что поток в трубе ламинарный, если

число Рейнольдса Re = pvd/m, не превышает 2000. Для болыших значений

числа Рейнольдса связь между перепадом давления и расходом становится нелинейной.

Принимая плотность воды 10-3 кг/см3, проверим корректность предположения о ламинарности потоков в трубах. Расходы на выходе из узлов 6, 7 и 8 равны 830, 350 и 480 см3/С; числа Рейнольдса изменяются от 3100 в элементе е5, до 40000 в элементе е6 и, следовательно, предположение о ламинарности потока некорректно.

40

Матричное исчисление

1.7. Функции Excel для операций над матрицами

Для выполнения операций с матрицами используются матричные функции Excel.

Категория: математические. Функции:

МУМНОЖ(<матрица1>;<матрица2>) – возвращает произведение матриц.

МОБР(<матрица>) – возвращает матрицу, обратную к данной.

МОПРЕД(<матрица>) – вычисляет определитель исходной квадратной матрицы.

Категория: ссылки и массивы. Функция: ТРАНСП(<матрица>) – транспонирует исходную прямоугольную матрицу, поворачивая ее относительно главной диагонали.

При выполнении операции следует:

ØВыделить блок, где будет размещен результат матричной операции.

ØВ мастере функций выбрать нужную категорию и нужную функцию.

ØУбрать окно соответствующей функции (с помощью кнопки

) или отбуксировать в сторону от исходных данных.

ØВыделить исходную матрицу (бегущая пунктирная линия).

ØОдновременно нажать клавиши Shift+Ctrl+Enter.

41

Численные методы решения задач линейной алгебры

Глава 2. Численные методы решения задач линейной алгебры

«75% всех расчетных математических

задач приходится на решение систем линейных алгебраических уравнений»

Е. Валях

Применение численных методов, в принципе, сводит все задачи к алгебраическим. Традиционно выделяют четыре основных задачи линейной алгебры:

∙решение систем линейных алгебраических уравнений (СЛАУ);

∙вычисление определителя;

∙нахождение обратной матрицы;

∙определение собственных значений и собственных векторов матрицы.

2.1. Системы линейных алгебраических уравнений

Системы линейных алгебраических уравнений могут либо непосредственно составлять задачу, которую необходимо решить

(канонические уравнения метода сил, метода перемещений, смешанного, комбинированного методов – в расчетах статически неопределимых систем; уравнения равновесия (баланс сил) – в расчетах статически определимых систем и др.), либо задача

сводится к решению системы линейных алгебраических уравнений той или иной структуры (краевые задачи, описываемые дифференциальными уравнениями, вариационные задачи и др.).

Система линейных алгебраических уравнений в общем случае имеет вид

42