Файловый архив студентов. Файловый архив студентов.
1306 вузов, 5174 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Пермский национальный исследовательский политехнический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ

.pdf
Скачиваний:
334
Добавлен:
29.03.2015
Размер:
2.5 Mб
Скачать
☆

Численные методы оптимизации

Во втором подходе используются методы, специально

разработанные для решения задач нелинейного программирования с ограничениями.

Мы рассмотрим лишь первый подход к решению этих задач, а именно методы сведения задач условной оптимизации к безусловной.

Эта операция выполняется с учетом прямых и функциональных ограничений. Устранение прямых ограничений

при переходе к безусловной оптимизации осуществляется соответствующим нормированием управляемых параметров.

При прямом ограничении а <ui< b нормирование можно выполнить, например, по формуле

é

u

i

- (b + a) / 2ù

 

 

xi = tgêp

 

 

ú

,

(8.106)

 

 

b - a

ë

 

 

û

 

 

преобразовав ограниченный параметр ui в неограниченный xi.

Функциональные ограничения устраняются путем конструирования обобщенной функции оптимизации с учетом типа ограничений. Так, если все ограничения представлены в

аналитическом виде и являются функциональными зависимостями типа равенств, то переход к задаче безусловной оптимизации

часто осуществляется с помощью метода неопределенных множителей Лагранжа [2, 20].

Метод множителей Лагранжа

В этом методе новая целевая функция – функция Лагранжа Ф(Х , L) —формируется из исходной целевой функции Z(X ) и всех функциональных ограничений типа равенств следующим образом:

 

m

 

ф( X , L) = Z(X ) + åλ jψ j (X ) ,

(8.107)

 

j=1

 

где L = (λ1,λ2 ,...,λm ) -

вектор неопределенных

множителей

Лагранжа; y j (X ) = 0 -

j-е ограничение типа равенства; т -

количество ограничений.

 

 

333

Численные методы оптимизации

Чтобы найти значения п неизвестных управляемых параметров x1, x2, ..., xп и m множителей Лагранжа l1 ,l2 ,...,lm ,

решается система алгебраических уравнений, выражающая необходимые условия экстремума функции Лагранжа:

ф(Х , L)

 

Z(X )

 

m

 

 

 

¶yi (X )

 

 

 

=

 

 

 

+ ål j

 

 

= 0 при i=1,2,…,n.

хi

xi

 

xi

 

 

 

j=1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(8.108)

ф(Х , L) = y j (X ) = 0

 

при j=1,2,…,m.

 

(8.109)

¶l j

 

 

 

 

 

 

 

 

 

 

 

 

 

Система уравнений разрешима, причем единственным

образом, относительно множителей Лагранжа, если

 

 

¶y1

L

¶y1

 

 

 

 

 

 

 

 

 

 

 

 

 

х

х

n

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

¹ 0 .

 

 

(8.110)

 

 

L

L

L

 

 

 

 

 

¶ym

 

L

¶ym

 

 

 

 

 

 

 

х

х

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

Функция Лагранжа Φ(Х , L) и целевая функция Z(X ) в

допустимой области

W совпадают,

так как здесь

Y( Х ) = 0 .

Поэтому если оптимальное значение функции Лагранжа найдено,

то оно будет одновременно и условным оптимумом целевой функции Z(X ) .

n Пример 8.11. Вернемся к задаче проектирования контейнера, оптимального с точки зрения затрат материала, т.е., имеющего минимальную поверхность (задача 8.1), и будем учитывать только ограничение-равенство, т.е математическая модель задачи нелинейного программирования имеет вид:

минимизировать

Zmin = 2(x1 x2

+ x2 x3 + x1 x2 )

при ограничении

х1х2 х3

=1.

Составим функцию Лагранжа для этой задачи:

Φ(Х , λ1 ) = 2(х1 х2 + х2 х3 + х1х3 ) + λ1 (х1х2 х3 −1) .

(8.111)

334

Численные методы оптимизации

В соответствии с (8.108) и (8.109) запишем необходимые условия минимума функции Лагранжа (8.111):

Φ(Х ,l1)

 

= 2х2 + 2х3 + l1х2 х3 = 0;

 

 

 

х1

 

 

 

 

 

 

 

 

Φ(Х ,l1)

 

= 2х

+ 2х

3

+ l

1

х х

3

= 0;

(8.112)

 

1

 

 

1

 

 

х2

 

 

 

 

 

 

 

 

Φ(Х , l1 )

= 2х + 2х

2

+ l

1

х х

2

= 0;

 

 

 

1

 

 

1

 

 

х3

 

 

 

 

 

 

 

 

Φ(Х , λ1 ) = х х

2

х

3

-1 = 0

1

 

 

λ1

 

 

 

 

Решение этой системы дает х1=х2=х3=1 м. Минимальное значение целевой функции равно 6 м2. Конструктивное ограничение - неравенство

(х1³1,5) в данном решении не удовлетворено, и следовательно, данное решение неприемлемо.

Кун и Таккер обобщили метод множителей Лагранжа на случай общей задачи нелинейного программирования (8.103) – (8.105) и построили необходимые условия оптимальности с ограничениями как в виде равенств, так и неравенств. Эти условия

оптимальности можно сформулировать в виде задачи нахождения решения некоторой системы нелинейных уравнений и неравенств, или, как иногда говорят, задачи Куна – Таккера. [2].

Найти векторы Х , u и L , удовлетворяющие следующим условиям:

m

l

 

ÑZ(X ) - åu j Ñg j (X ) - ålk Ñhk (X ) = 0 ,

 

j=1

k =1

 

g j (X ) ³ 0 ,

j=1,2,…,m;

 

hk (X ) = 0 ,

k=1,2,…,l;

(8.113)

u j g j (X ) = 0 ,

j=1,2,…,m;

 

u j ³ 0 ,

j=1,2,…,m.

 

335

Численные методы оптимизации

Решая систему уравнений и неравенств (8.113), находим

как искомые переменные Х , так и вспомогательные переменные – множители Лагранжа uj и lk.

При этом для активных ограничений-неравенств, выполняемых в точке оптимального решения в виде равенств gj=0,

множители Лагранжа u j ³ 0 , а для неактивных ограничений (gj>0)

выполняются условия ujgj=0, то есть, для этих ограничений uj=0. Если существует возможность обнаружить ограничения,

которые неактивны в точке оптимума, до непосредственного решения задачи, то эти ограничения можно исключить из модели и тем самым уменьшить ее размеры.

n Пример 8.12. Снова обратимся к задаче проектирования контейнера, имеющего минимальную поверхность (задача 8.1), но с учетом всех ограничений:

минимизировать

 

 

 

 

Zmin

= 2(x1 x2

+ x2 x3

+ x1 x2 )

 

при ограничении – равенстве

 

 

х1х2 х3

=1

 

 

и ограничениях – неравенствах: х1 ³ 1,5; х2 ³ 0; х3 ³ 0.

 

 

 

 

 

 

Составим задачу Куна – Таккера (8.113):

 

 

Z

 

 

 

æ ¶g j

ö

 

h

 

 

 

 

 

 

 

 

 

 

- åu j çç

 

 

 

 

÷÷

- ålk

 

k

 

= 2x2 + 2x3 -u1

- lx2 x3 = 0 ,

 

 

x

 

 

x

 

 

x

 

1

 

 

 

è

 

 

1

ø

 

1

 

 

 

 

 

 

Z

 

 

 

æ ¶g j ö

 

 

h

k

 

 

 

 

 

 

 

 

-

åu j çç

 

 

 

÷÷

- ålk

 

 

= 2x1 + 2x3 -u2

- lx1x3 = 0 ,

 

 

x2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

è

 

x2 ø

 

 

x2

 

 

 

 

 

 

Z

 

 

 

æ ¶g j ö

 

 

h

k

 

 

 

 

 

 

 

 

-

åu j çç

 

 

 

÷÷

- ålk

 

 

 

= 2x1 + 2x2 - u3

- lx1x2 = 0 ,

(8.114)

 

x3

 

 

 

 

 

x3

 

 

 

 

 

è

 

 

x3 ø

 

 

 

 

 

 

 

х1 - 1,5³0; x2>0;

 

 

 

x3>0;

 

 

 

 

 

 

 

 

 

х1х2 х3 -1 = 0 ;

 

 

 

 

 

 

 

 

 

 

 

 

 

u1 ³ 0 ; u2=0;

 

u3=0.

 

 

 

 

 

 

 

 

Решая данную систему уравнений и неравенств, получаем х1=1,5; х2=х3=0,816. Целевая функция при этих значениях Zmin=6,232.

336

Численные методы оптимизации

Метод штрафных функций

Основная идея метода штрафных функций состоит в

преобразовании задачи нелинейного программирования с

ограничениями [3, 33]

Z= Z(X ) , Х Ω

Ω: g j (X ) ≤ 0,

( j =1,2,...,m) ,

(8.115)

h j (X ) = 0

, (j=1,2,…l)

 

либо в одну задачу без ограничений (эквивалентную исходной),

либо в эквивалентную последовательность задач поиска минимума без ограничений функции

F(X ) = Z(X ) + ϕk (X ) → min , Х Еп ,(k=1,2,…,),

(8.116)

где ϕk (X ) – функция, которая называется штрафной функцией.

G Замечание. Ограничение вида "меньше или равно", g (х) ≤ 0, всегда может быть записано как –g (х) ³ 0, поэтому в приведенной выше формулировке нет потери общности.

Штрафная функция строится таким образом, чтобы при нарушении ограничений эта функция "штрафовала" функцию

F(X ) , т. е. увеличивала ее значение. Функция ϕk (X ) , удовлетворяющая этому условию, может быть не единственной.

Среди методов штрафных функций выделяют методы

внешней точки и методы внутренней точки (которые иногда еще называют методами барьерных функций).

В методах внешней точки в качестве функции штрафа выбирают функцию, которая с ростом k во все большей степени учитывает ограничения, определяющие множество Ω исходной

задачи, например,

 

 

 

 

ϕk (X ) = kϕ(X ) ,

 

(8.117)

 

l

m

2

 

где

ϕ(X ) = åg 2j

( X ) + å[g +j (X )]

,

 

j=1

j=l +1

 

 

337

Численные методы оптимизации

g +j

При

больших

ì

 

если

g j (X ) £ 0

 

ï0,

 

 

(X ) = í

 

(X ),если

g

 

(X ) > 0

 

ïg

j

j

 

î

 

 

 

 

определенных условиях, а именно, при

достаточно

k последовательность решений задач

безусловной

минимизации (8.116), (8.117) сходится к решению Х * задачи (8.115), поэтому полагают Х * » Х k , Z * » Z(X (k) ) .

Критерием достижения требуемой точности решения задачи

(8.115) может служить неравенство:

 

x(k ) - x(k / 2) £ e

(8.118)

где e>0 – число, характеризующее точность, k – четное число.

n Пример 8.13. Решить задачу 8.3 методом штрафных функций,

математическая модель которой имеет вид

 

Z min =

x1

+ cx2 ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x2

 

 

 

 

 

 

 

 

 

 

х1–1 ³0;

 

 

 

 

 

 

 

 

 

 

х1х2–1 ³ 0;

 

 

 

 

 

 

 

 

 

 

х1 ³ 0,

 

х2 ³ 0.

 

 

 

 

 

 

Составим вспомогательную функцию F(X )

(8.115) в соответствии

с выражением (8.117) для случая с=0,5:

 

 

 

 

 

 

F(X ) =

x1

+ 0,5x

2

+ k(x

-1)

2 + k(x x

2

-1)2 .

 

 

 

x2

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В табл. 8.6 приведено решение для некоторых k. Точное решение

задачи: х1=1; х2=1; Z=1,5.

 

 

 

 

 

 

 

 

Таблица 8.6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

 

 

x1

 

 

 

 

x2

 

 

 

F(x1,x2)

1

 

0,708

 

 

 

 

 

1,319

 

 

 

1,286

2

 

0,798

 

 

 

 

 

1,255

 

 

 

1,345

50

 

0,985

 

 

 

 

 

1,019

 

 

 

1,488

100

 

0,993

 

 

 

 

 

1,01

 

 

 

1,498

500

 

0,998

 

 

 

 

 

1,002

 

 

 

1,499

1000

 

0,999

 

 

 

 

 

1,001

 

 

 

1,499

338

Численные методы оптимизации

Использование методов внутренней точки позволяет удерживать траекторию поиска внутри допустимой области с

помощью так называемой барьерной функции ϕk (X ) , которую часто выбирают в виде [3]:

 

1

m

1

 

 

ϕk (X ) =

å

.

(8.119)

k

 

 

j=1

g j (X )

 

В этом случае важен выбор начальных значений вектора X и параметра k, что представляет непростую задачу и является главным недостатком этого метода.

Преимущество применения метода штрафных функций для решения задач нелинейного программирования состоит в том, что

поиск минимума может осуществляться методами безусловной оптимизации, такими, например, как метод покоординатного или градиентного спуска.

8.5. Решение задач оптимизации с помощью электронных таблиц Excel

Решение задач оптимизации в Microsoft Excel производится с

помощью надстройки «Поиск решения». В процедуре поиска решения Excel используется алгоритмы нелинейной оптимизации

методов сопряженных градиентов и Ньютона, описанные выше,

а также алгоритмы симплексного метода и метода «branch-and- bound» для решения линейных и целочисленных задач с

ограничениями

Принципы построения схемы задачи в таблице и решения задач линейного и нелинейного программирования практически совпадают.

При поиске оптимального решения задачи можно изменять условия и варианты поиска решения для линейных и нелинейных задач, ипользуя диалоговое окно «Параметры поиска решения». Пользователь при этом может сам выбрать алгоритм оптимизации.

Рассмотрим процесс решения задач оптимизации на прмерах двух задач: задачи планирования производства, и

339

Численные методы оптимизации

транспортной задачи (пример 8.8), используя возможности таблиц Excel.

8.5.1. Решение задачи планирования производства

Рассмотрим задачу, приведенную в примере 8.6.

Целевая функция

zmin = 1− x1 − x2 ,

 

x1 - x2 +1 ³ 0

Ограничения:

3x1 + 2x2 - 6 ³ 0,

- 3x1

- x2

+ 9 ³ 0,

 

x1 ³ 0,x2 ³ 0.

Порядок решения

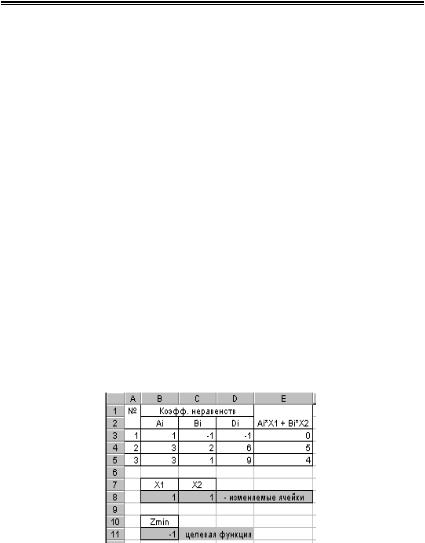
1. Подготовим таблицу как показано на рис.8.21. Ячейки, содержащие целевую функцию (В11) и изменяемые ячейки (проектные параметры Х1, Х2) В8:С8 тонируем. Для контроля счета в ячейки В8:С8 введем единицы. Значения проектных параметров х1=1 и х2=1 можно рассматривать как нулевое приближение решения задачи.

Рис.8.21. Схема задачи

2.В ячейки В3:D5 введем коэффициенты системы ограничений

3.В ячейку E3 введем формулу для вычисления левой части 1- го ограничения, т.е. E3=СУММПРОИЗВ($B$8:$C$8;B3:C3), и

340

Численные методы оптимизации

после ввода скопируем ее вниз до конца таблицы. Будет не лишним проверить результаты счета для заданных значений х1=1 и х2=1.

4.Формулу целевой функции запишем в ячейке В11: =1-В$8-

С$8.

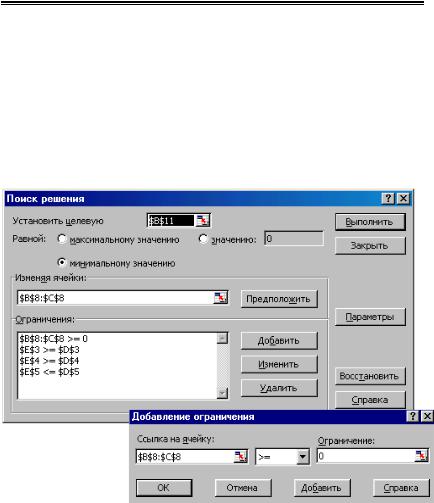
5.Выберем команду меню Сервис\Поиск решения и в появившемся окне сделаем соответствующие установки. Ограничения устанавливаются с помощью кнопки Добавить, которая вызывает окно для ввода этих ограничений (рис.8.22).

Рис.8.22. Окно «Поиск решения»

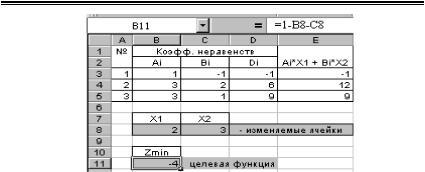
6. После щелчка на кнопке Выполнить при условии, что введено все верно, результат решения будет иметь вид, как показано на рис.8.23.

341

Численные методы оптимизации

Рис.8.23. Результаты решения

Результаты можно сохранить или отказаться от них (восстановив исходные значения). Можно получить один из видов отчетов (Результаты, Устойчивость, Пределы). Отчет можно оформить на отдельном листе Книги с соответствующим именем.

8.5.2. Решение транспортной задачи

Рассмотрим задачу, приведенную в примере 8.8.

Целевая функция:

zmin =3x11+5x12+7х13+11х14+x21+4x22+6x23+3x24+5x31+8x32+12x33+7x34.

Ограничения:

x11 +x12 +х13+х14=150, x21 +x22 +x23+x24=130,

x31 +x32.+x33+x34=170, x11 +x21 +х31=150,

x12 +x22 +x32=120, x13 +x23.+x33=80, x14 +x24.+x34=50,

xij³0 (i=1,2,3; j=1,2,3,4).

Порядок решения

1. Подготовим таблицу, как показано на рис.8.24. Ячейки, содержащие целевую функцию J10 и изменяемые ячейки

(проектные параметры xij, i=1,2, j=1,2,3) D4:D6, F4:F6; Н4:Н6, J4:J6, тонированы. Для контроля счета в изменяемые ячейки введем

342

Соседние файлы в папке Информатика 2 сессия
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности