Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ

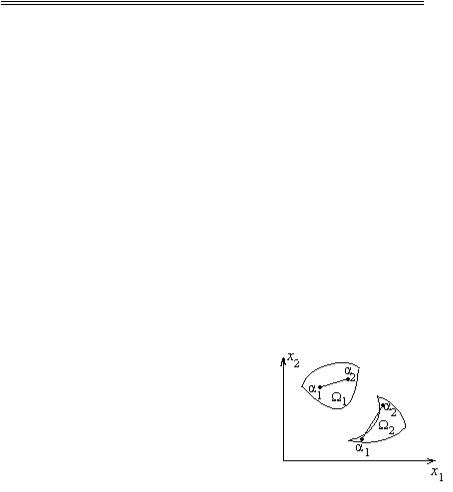
Численные методы оптимизации

8.4. Нелинейные задачи оптимизации

Большинство практических задач оптимизации приводит к

нелинейным целевым функциям и ограничениям.

Для решения нелинейных задач оптимизации предложено достаточно много алгоритмов, но ни один из этих алгоритмов не имеет по отношению к другим таких преимуществ, чтобы его можно было считать универсальным средством решения (как в линейном программировании – симплекс-метод). Это связано с тем, что при решении нелинейных задач оптимизации может получиться много локальных экстремумов (см. рис.8.1), из которых надо выбирать глобальный. Во многих практических задачах для определения того, при каких условиях локальное оптимальное решение является также и глобальным, оказываются полезными такие понятия, как выпуклость и вогнутость функций и множеств.

8.4.1. Выпуклые множества и выпуклые функции

Множество Ω называется выпуклым в n-мерном пространстве, если для любой пары точек α1 и α2, принадлежащих этому множеству, отрезок прямой, соединяющей их, также полностью принадлежит этому множеству. На рис.8.15 множество Ω1 является выпуклым, а множество Ω2 – невыпуклым.

основании которой лежит правильный многоугольник.

Выпуклые функции играют большую роль во многих вопросах оптимизации в связи с тем, что всякий локальный минимум выпуклой функции является одновременно и глобальным.

Функцию назовем выпуклой книзу, если она определена на

выпуклом множестве и значение ее в любой промежуточной точке

313

Численные методы оптимизации

любого отрезка [х1 х2]Ω связано со значениями на концах

отрезка неравенством

Z(xi ) ≤ (1 − ν)Z(x1 ) + νZ(x2 ) , где 0 ≤ ν ≤1 . (8.88)

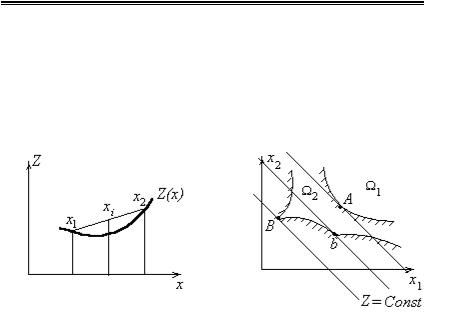
На рис.8.16 поясняется свойство выпуклости функции одного переменного: график функции проходит всегда не выше отрезка прямой, соединяющей вершины любой пары ее ординат.

Если целевая функция линейна, а допустимая область выпукла Ω1, то существует единственный глобальный минимум на границе области (на рис.8.17 точка А). Если же допустимая область – невыпуклое множество, то на границе могут иметь место локальные экстремумы. И если строить алгоритм движения вдоль невыпуклой границы допустимой области Ω2 к оптимальной системе, то можно попасть в точку локального минимума (точка b), не отличая ее от глобального минимума (точка В). Сходимость такого метода часто нельзя обосновать.

8.4.2. Классификация численных методов решения нелинейных задач оптимизации

По ряду признаков методы поиска экстремума могут быть отнесены к тому или иному классу.

- В зависимости от типа искомого экстремума различают методы глобальной и локальной оптимизации.

314

Численные методы оптимизации

-В зависимости от того, как при поиске экстремума функции учитываются ограничения на переменные, различают методы безусловной и условной оптимизации.

-В зависимости от количества управляемых параметров

целевой функции различают методы одномерного и многомерного поиска.

Методы поиска глобального экстремума в настоящее время являются предметом интенсивных исследований.

Надежные и одновременно экономичные методы поиска глобального экстремума в настоящее время неизвестны.

Надежным, но крайне неэкономичным методом глобального поиска является метод сканирования (или метод

сеток). При его применении область определения Z(X ) в

пространстве управляемых параметров разбивается на k подобластей, в центре каждой из которых вычисляется значение целевой функции. Если функция зависит от n параметров, то необходимо выполнить kn вариантов расчетов. Чтобы получить

достоверную картину поведения гиперповерхности отклика целевой функции, необходимо сканировать допустимую область с достаточно малым шагом. Поэтому даже для сравнительно

несложных задач потери машинного времени на поиск становятся очень большими.

Этот недостаток характерен и для методов случайного поиска глобального экстремума. Однако затраты ресурсов на случайный поиск можно сделать приемлемыми, если не

предъявлять высоких требований к надежности определения экстремума. Чаще всего данный метод применяют для задач, содержащих не более трех управляемых переменных.

Большинство используемых методов, как правило, являются

методами локального поиска. На практике предположение о том, что локальный экстремум является глобальным, может быть

проверено путем использования нескольких начальных векторов (точек). Но даже если в каждом из этих случаев получится одно и то же локальное решение, в общем случае нельзя показать, что это решение обязательно является глобальным оптимумом. К счастью для задач, соответствующих реальным физическим процессам,

315

Численные методы оптимизации

целевая функция обычно является "хорошей" и обладает единственным экстремумом. Поэтому для большинства практических целей использование численных процедур, дающих локальный экстремум, не является большим недостатком.

Наиболее многочисленную группу методов локального поиска составляют методы безусловной оптимизации.

Некоторое представление о широко применяемых методах этой группы дает рис. 8.18.

Взависимости от порядка используемых производных

целевой функции по управляемым параметрам методы безусловной оптимизации делят на методы нулевого, первого и второго порядков.

Вметодах нулевого порядка (прямых методах) информация

опроизводных не используется.

Для методов первого порядка необходимо вычислять как значение целевой функции, так и ее первые частные производные

(градиентные методы).

В методах второго порядка организация поиска экстремума ведется с учетом значений целевой функции, ее первых и вторых производных.

Одномерный поиск может рассматриваться как самостоятельная задача, если аргументом целевой функции является один параметр Z=Z(x).

Этот же поиск может использоваться в качестве части процедуры многомерной оптимизации (когда количество управляемых параметров два и более) в тех случаях, когда необходимо найти оптимальный шаг в выбранном направлении.

Часто задачи условной оптимизации преобразуют в задачи

безусловной оптимизации с помощью методов Лагранжа или

штрафных функций. После этого к ним можно применять методы безусловной оптимизации.

316

Численные методы оптимизации

Локальные методы безусловной оптимизации

Рис.8.18. Классы методов безусловной оптимизации

Известны также методы условной оптимизации, например, такие как методы проекции градиента, допустимых направлений, метод Заутендайка [44] и др.

Основные этапы поиска экстремума

Для конкретизации дальнейшего изложения будем считать, что в процессе оптимизации ищется минимум целевой функции.

Практически во всех методах оптимизации стремятся

обеспечивает сходимость и можно надеяться, что минимум функции будет найден.

317

Численные методы оптимизации

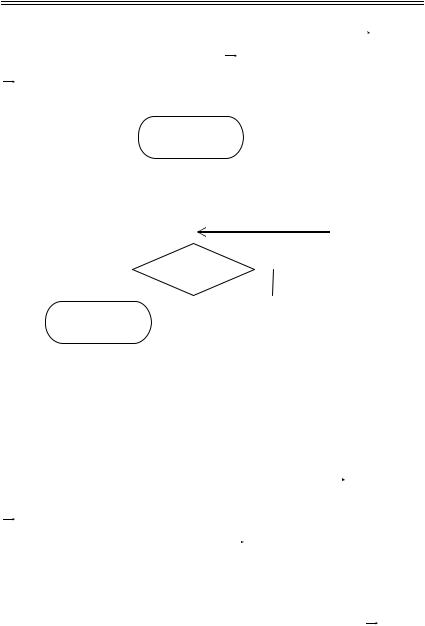
Численные методы поиска оптимума позволяют построить такую последовательность шагов от начальной точки Х 0 через некоторые промежуточные точки Х k к локальному экстремуму

Х * . Схема алгоритма поиска для общего случая показана на рис.8.19.

1. Начало

поиска

Рис. 8.19. Основные этапы алгоритма поиска экстремума

Как отмечалось выше, выбор исходной точки Х 0 поиска во многом определяет успех решения всей задачи. Очевидно, что

Х0 должна принадлежать области определения целевой функции,

ичем ближе к экстремуму выбрана Х 0 , тем быстрее и с большей вероятностью экстремум будет найден.

Сущность метода оптимизации определяется этапами 4 и 5 алгоритма, на которых выбирается направление дальнейшего

поиска и вычисляются координаты очередной точки Х k+1 на

318

Численные методы оптимизации

траектории поиска. Далее в точке Х k+1 вычисляются значения целевой функции Z(Х k +1 ) и функций-ограничений, т. е.

определяется информация, позволяющая судить о достигнутом успехе. Исследователь может назначить различные условия прекращения поиска, и в зависимости от степени их выполнения поиск будет продолжен или прекратится.

Важной характеристикой методов является их скорость сходимости. Однако оценка сходимости того или иного метода

обычно базируется на некоторых теоретических предпосылках относительно особенностей целевой функции (например, функция дважды непрерывно дифференцируема или сильно выпукла), а также зависит от выбора начальной точки поиска.

8.4.3. Численные методы одномерного поиска

Рассмотрение методов оптимизации удобно начинать с одномерного случая, т.е. функций, аргументом которых является один параметр Z=Z(x).

Существование локальных минимумов функции Z(x), отличных от глобального, почти всегда затрудняет поиск решения х*, поэтому многие приближенные (численные) методы минимизации применимы только тогда, когда любой локальный минимум Z(x) является одновременно и глобальным. Один из классов функций, удовлетворяющих этому условию, составляют

унимодальные (одноэкстремальные) функции.

Методы, рассматриваемые далее, строятся в предположении унимодальности функции Z(x) на заданном интервале отрезка [а,b]. Обозначим через х* искомое значение управляемого параметра, доставляющего минимум целевой функции Z(x). К

функции не предъявляются требования дифференцируемости или непрерывности. Предполагается, что для любого х [а,b] значение Z(x) может быть вычислено, т. е. найдено путем вычислительного эксперимента.

Методы одномерного поиска можно разделить на:

319

Численные методы оптимизации

1.Методы последовательного поиска (методы перебора,

дихотомии, золотого сечения и др.);

2.Методы, использующие аппроксимацию функции

(методы квадратичной и кубической интерполяции и др.).

Рассмотрим некоторые из этих методов.

Метод перебора или равномерного поиска

Данный метод является простейшим из прямых методов минимизации и состоит в следующем:

Отрезок [a,b] разбивается на n равных частей точками

Вычислив значения Z(x) в точках xi, путем сравнения находится точка xm (где m – число от 1 до n) такая, при которой Z(xm)=minZ(xi) для всех i от 1 до n.

Погрешность ε определения точки минимума xm функции Z(x) методом перебора не превосходит величины ε=(b-a)/n.

Метод дихотомии (или половинного деления)

Идея метода заключается в том, чтобы на каждом шаге итерации (n = 1, 2,…) целевая функция Z(х) вычислялась только в двух точках, и при этом вдвое уменьшалась интервал неопределенности (ИН).

Исходя из свойства унимодальности функции, можно

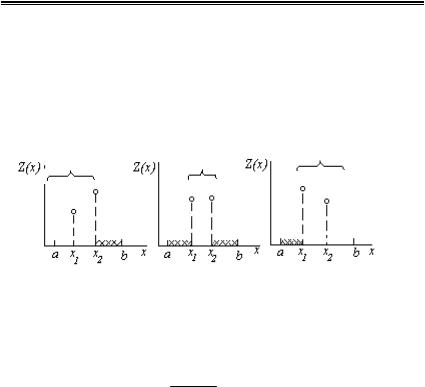
построить такую стратегию последовательного поиска точки минимума х*, при которой любая пара опытов (вычислений Z(х)) позволяет сузить область поиска (или интервал неопределенности). В самом деле, вычисляя Z(x) в точках x1 и х2 таких, при которых а < x1 < х2 < b, можно локализовать интервал

неопределенности путем анализа полученных значений функции

(рис.8.20) [20]:

320

Численные методы оптимизации

При этом можно построить последовательность вложенных

отрезков [a, b] É [a1, b1] É … É [an-1, bn-1] É [an, bn], каждый из которых содержит точку минимума х* функции Z(x).

Стратегия выбора значений x1 и x2 для проведения опытов с

учетом предыдущих результатов определяет сущность различных методов последовательного поиска.

Рис.8.20. Влияние парного эксперимента на определение области поиска.

В частности, в методе дихотомии этот выбор производится следующим образом:

1) Вычисляется срединная точка интервала

xm = an + bn

2

2) Определяются координаты двух точек слева и справа вблизи

где e>0 – требуемая точность определения точки х*.

3)Вычисляются значения целевой функции в этих точках Z(x1) и Z(x2) и сравниваются в соответствии с условиями (8.90).

4)Если (bn-аn)< e, то поиск прекращается, в противном случае выполняется следующая итерация.

Для n = 0, 1, 2,… можно записать последовательности вычисления {an}, {bn}, {x1(n)}, {x2(n)}, используя рекуррентные

формулы:

321

Численные методы оптимизации

Используя условие εn <ε, из последнего выражения можно найти необходимое число шагов n для обеспечения требуемой точности ε. Однако на практике часто поступают иначе: определив границы отрезка [an, bn], вычисляют εn по формуле (8.92) и сравнивают с заданной точностью ε.

n Пример 8.8. Найти минимальное значение Zmin и точку минимума х* функции Z(x) = x4 − 5x2 + e− x на отрезке [1,5; 2]. Точку х* найти с погрешностью ε = 0,05.

Решение. Построим последовательность вложенных отрезков [an, bn] по формулам (8.91), записывая результаты вычислений в табл. 8.4.

Таблица 8.4

322