Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ

Матричное исчисление

1.3. Действия над матрицами

Действия над матрицами определяются с помощью действий над их элементами.

1) Сумма (разность) двух матриц одинакового типа А±В есть матрица С того же типа:

C= A ± B = [aij ± bij ].

2)Произведение матрицы A = [aij ]на число a есть матрица,

элементы которой получены умножением всех элементов на число a: αA = [αaij ].

3) Произведением матрицы A = [aij ] размера [m´n] на матрицу B = [bij ] размера [n´r] называется матрица C = [cij ] размера

n

[m´r], элементы которой вычисляются по формуле cij = åaik bkj .

k =1

То есть , чтобы получить элемент cij , стоящий в i -й строке и в j-м

столбце матрицы С, нужно элементы i -й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить.

Произведение А×В двух матриц в указанном порядке возможно в том и только в том случае, когда число столбцов

матрицы А равно числу строк матрицы В.

4) Произведение матрицы А на вектор X – частный случай произведения матрицы на матрицу, когда второй сомножитель является матрицей-столбцом (или вектором), причем

количество элементов вектора X должно быть обязательно равно количеству столбцов матрицы А. Результатом перемножения

n

является вектор B (А X = B , где bi = åaij × x j ).

j=1

23

Матричное исчисление

5) Дифференцирование матриц выполняется посредством дифференцирования каждого ее элемента, т.е.

Действия над матрицами подчиняются следующим законам:

1)А+В = В+А;

2)А+(В+С) = (А+В)+С;

3)a(А+В)= aА+aВ;

4)a(bА)=( ab)А;

5)A(BC) = (AB)C;

6)(А+В)С = АС + ВС;

7)С(А+В) = СА + СВ ;

8)α(АВ) = (αА)В=А(aВ).

Основной особенностью матричного исчисления является некоммутативность произведения матриц:

АВ ¹ ВА,

т.е. произведение двух матриц не обладает свойством

переместительности и из существования произведения АВ вовсе не следует существование произведения ВА. Покажем это на примере.

nПример 1.1. Вычислить произведение двух матриц А и В.

24

Матричное исчисление

1.4. Нормы матрицы и вектора

Норма – это одна из важнейших скалярных характеристик векторов и матриц. Существуют различные способы измерения нормы матрицы и вектора соответственно. В дальнейшем для анализа решений нам потребуется умение вычислять эти нормы.

Матрица A = [aij ]определяется тремя нормами:

– максимальная сумма модулей элементов матрицы по строкам;

– максимальная сумма модулей элементов матрицы по столбцам;

– корень квадратный из суммы квадратов модулей всех элементов.

nПример 1.2. Для матрицы А вычислить нормы A1 , A 2 , A 3 .

Решение:

A1 = max (3+2+4, 5+2+6, 0+7+1) = max (9, 13, 8) =13;

A 2 = max (3+5+0, 2+2+7, 4+6+1) = max (8, 11, 1) = 11;

25

1.5. Матрицы в задачах строительной механики

Расчет реальных строительных сооружений чаще всего производится с применением ЭВМ. Использование матричного

языка линейной алгебры позволяет компактно в виде матричного алгоритма излагать методы строительной механики, а также

помогает инженеру более широко смотреть на многие проблемы расчетов, видеть их существо, не вдаваясь в детали, в смысл каждой арифметической операции.

Расчет в матричной форме является универсальным, приемлемым для любого вида конструкций. В состав сооружения

26

Матричное исчисление

могут входить такие конструктивные элементы, как стержни, пластины и оболочки различной формы, массивные тела. Использование матриц требует дискретизации расчетной схемы. С

этой точки зрения матричная формулировка задачи особенно удобна при расчете стержневых систем, для которых дискретная расчетная схема является наиболее естественной.

Удобство представления конструкции дискретной расчетной схемой при использовании ЭВМ привело к тому, что эту схему распространили и на расчет континуальных систем типа пластин, оболочек и массивных тел. Широкая реализация этой идеи привела к методу конечных элементов (глава 7), который появился в начале пятидесятых годов ХХ столетия. Примерно в это же время активно стала внедряться матричная форма расчета.

Поясним смысл матричных операций на простейших задачах строительной механики.

1.5.1.Матрицы влияния внутренних сил

Врасчетах стержневых систем нас всегда интересует связь между внешними силами, действующими на систему, и внутренними усилиями, возникающими в отдельных сечениях или элементах конструкции.

Для линейно деформируемых систем справедлив принцип независимости действия сил (суперпозиции) и любое внутреннее усилие Si, (в i-м сечении или элементе конструкции) от действия нескольких нагрузок P1, P2, ..., Pn может быть представлено в виде алгебраической суммы усилий от каждой нагрузки Pj в отдельности:

Поскольку, по правилам линейной алгебры произведение строки на

столбец равно алгебраической сумме попарных произведений их элементов, выражение (1.10) можно записать в виде

27

Матричное исчисление

Вычисляя внутренние усилия в нескольких (m) сечениях или элементах от действия той же группы внешних нагрузок P1, P2, ..., Pn, можно записать следующие выражения (линейные преобразования):

Sm = sm1P1 + sm2P2 +K+ smn Pn .

Здесь sij представляют собой усилия, возникающие i -м сечении от силы Pj=1.

Эти же уравнения также могут быть записаны в виде

Таким образом, формулы (1.10), (1.11) являются различными формами записи линейного преобразования вектора нагрузки P в

вектор внутренних усилий S . Матрица этого преобразования LS

называется матрицей влияния внутренних сил и является полной характеристикой линейного преобразования (1.11 б).

Составление этой матрицы эквивалентно решению в общем виде задачи вычисления внутренних усилий (изгибающих

28

Матричное исчисление

моментов M, поперечных сил Q, продольных сил N) в заданной конструкции от нагрузки заданного вида.

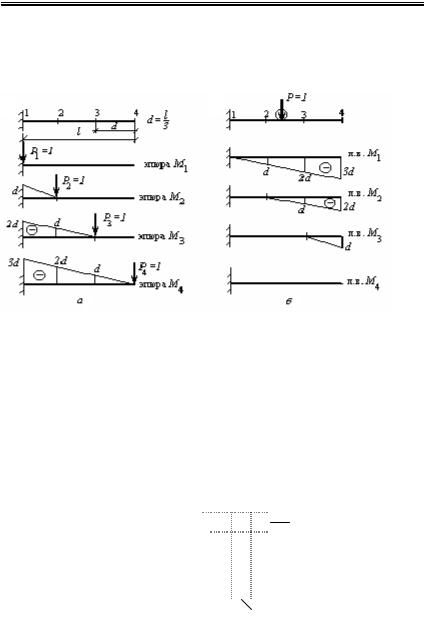
nПример 1.4. Построим матрицу влияния изгибающих моментов в

консольной балке от сосредоточенной нагрузки (рис.1.1,а).

Рис.1.1. К построению матрицы влияния изгибающих моментов в

балке

Поделив пролет l на три равные части длиной d, построим эпюры изгибающих моментов, прикладывая единичную силу последовательно в сечениях 1, 2, 3 и 4 (рис.1.1,а).

Поскольку элементы sij матрицы влияния Lm – это усилия, возникающие в i-м сечении от силы Pj=1, то первый столбец этой матрицы состоит из ординат единичной эпюры M1, второй – из ординат

29

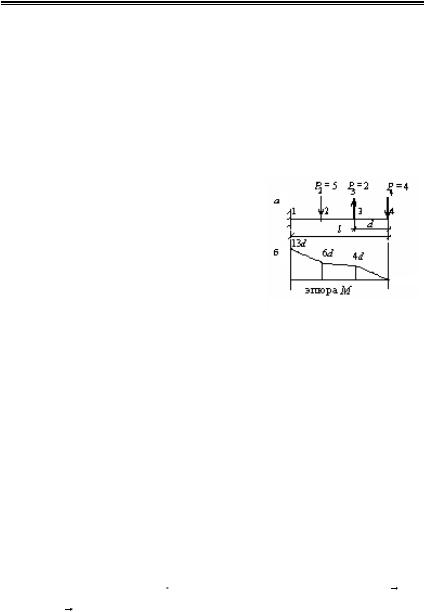
Матричное исчисление

Таким образом, столбцы матрицы влияния представляют собой

ординаты эпюр, а строки этой же матрицы являются ординатами линий влияния М1, М2, М3 и М4, соответственно. Это видно из рис.1.1,б.

Спомощью матрицы влияния можно вычислить внутренние усилия

врассмотренных сечениях от любой вариации приложенных внешних нагрузок.

nПример 1.5. Определим изгибающие моменты при действии на балку нагрузки, показанной на рис.1.2, а.

Рис.1.2.Нагрузки , действующие

на балку

Эпюра изгибающих моментов, соответствующая данному случаю, показана на рис.1.2,б.

Для более сложных конструкций матрицы влияния будут более громоздкими. Однако ход их построения аналогичен. Следует отметить, что если матрица влияния L составлена для нагрузки из сосредоточенных сил, приложенных к сооружению на одной линии, то элементы каждой строки этой матрицы представляют собой ординаты соответствующих линий влияния.

При расчетах сложных систем на ЭВМ это можно использовать для получения линий влияния Si по точкам.

В строительной механике часто решаются взаимно обратные задачи. Например, наряду с задачей вычисления

изгибающих моментов М (или других внутренних усилий S ) от нагрузки Р можно поставить задачу вычисления сил Р1, Р2,…, Рn

30

Матричное исчисление

по заданным внутренним усилиям, т.е. вычислить коэффициенты следующего линейного преобразования:

P1 = b11S1 + b12S2 +K+ b1nSn ;

P2 = b21S1 + b22S2 +K+ b2nSn ;

............................................. (1.12)

Pn = bn1S1 + bn2S2 +K+ bnnSn .

Преобразование (1.12) называется обратным по отношению к (1.11), а его матрица В является обратной по отношению к матрице

1.5.2. Матричная форма расчета статически определимых ферм

При расчете ферм матрицу влияния удобнее получать, составляя вначале уравнения (1.12), которые представляют собой

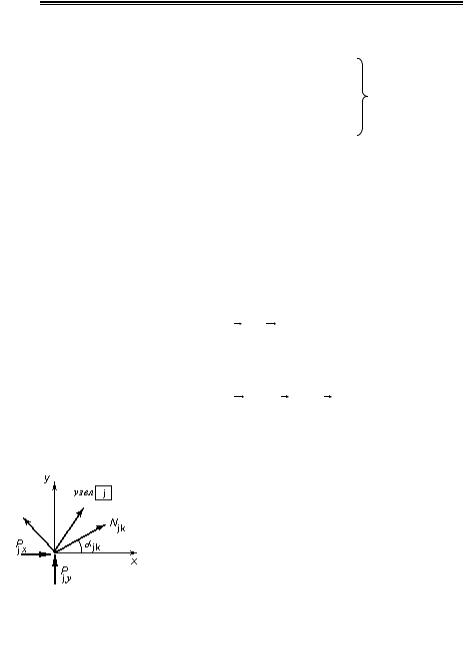
Уравнения равновесия узлов фермы (1.15) составляются в виде проекций сил на оси Х и У для каждого узла (рис. 1.3 ):

всего 2k уравнений (k – число узлов).

Рис.1.3. К условию равновесия j-го узла

фермы

31

Матричное исчисление

Здесь суммы содержат столько слагаемых, сколько стержней примыкает к рассматриваемому j-му узлу;

N – вектор неизвестных усилий в стержнях системы (включая опорные стержни), а элементами матрицы В являются синусы и косинусы углов наклона стержней к оси Х (рис.1.3).

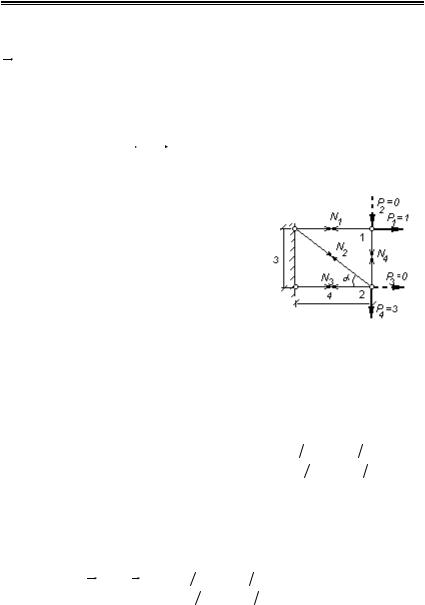
nПример 1.6. Для фермы (рис.1.4) составим матрицу В обратного

Тогда внутренние усилия в стержнях фермы от действия внешней нагрузки легко определятся по формуле (1.16)

32