
Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ
.pdf
Численные методы оптимизации
две группы выходных параметров. В первую группу входят выходные параметры, значения которых в процессе оптимизации
нужно увеличивать yi+ (X ) , во вторую – выходные параметры, значения которых следует уменьшать yi− (X ) .
Например, при проектировании какого-либо микрорайона решается ряд задач:
1)проектирование жилой застройки, где в качестве критерия выбран
максимум числа поселяемых жителей; проектирование торговых центров, где критерием выбран максимум пропускной способности магазинов и т.д.;
2)прокладка транспортных маршрутов, где в качестве критерия выбрано минимальное время нахождения пассажиров в пути; проектирование сетей теплоснабжения, где критерием является
минимум теплопотерь на трассе.
Объединение нескольких выходных параметров, имеющих в общем случае различную физическую размерность, в одной
скалярной целевой функции требует предварительного нормирования этих параметров. Способы нормирования параметров будут рассмотрены ниже. Пока будем считать, что все
y(X ) безразмерны и среди них нет таких, которым соответствуют
условия работоспособности типа равенства. Тогда для случая
минимизации целевой функции свертка векторного критерия
будет иметь вид
q |
m |
|
Z(X ) = åa j y−j (X ) − |
åa j y+j (X ) , |
(8.9) |
j=1 |
j=q+1 |
|
где aj >0 –весовой коэффициент, определяющий степень важности j-го выходного параметра (обычно aj выбираются
проектировщиком и в процессе оптимизации остаются постоянными).
В случае, когда все или основные условия работоспособности (8.8) имеют вид равенств, целевую функцию
(8.1), выражающую аддитивный критерий, можно записать
273

Численные методы оптимизации
m |
|
Z(X ) = åa j [ y j (X ) − yTTj (X )]2 . |
(8.10) |
j=1
Вэтом случае целевая функция определяет среднеквадратичное приближение yi (X ) к заданным техническим требованиям TTj.
Мультипликативный критерий [44] может применяться в тех случаях, когда отсутствуют условия работоспособности типа
равенств и выходные параметры не могут принимать нулевые значения. Тогда минимизируемая мультипликативная целевая
функция имеет вид
q |
m |
|
Z(X ) = Õ y−j |
( X ) / Õ y+j (X ) . |
(8.11) |
j=1 |
j=q+1 |
|
Наиболее существенными недостатками как аддитивного,
так и мультипликативного критерия является неучет в постановке задачи технических требований, предъявляемых к выходным параметрам, а также то, что здесь в принципе недостаток в одном критерии может быть скомпенсирован за счет другого. Например, недостаточная комфортность жилища за счет стоимости здания.
Критерии подобного типа напоминают предложенный в шутку Л.Н.Толстым "критерий для оценки человека", в виде дроби: в
числителе дроби стоят действительные достоинства человека, а в знаменателе – его мнение о себе. Несостоятельность такого критерия очевидна, так как по нему человек, почти не имеющий достоинств, но совсем не обладающий самомнением, будет иметь бесконечно большую ценность.
Критерий формы функции обычно используют, когда ставится задача наилучшего совпадения заданной (эталонной)
характеристики уТТ (Х ,ω) с соответствующей выходной характеристикой у (Х ,ω) проектируемого объекта. Здесь ω –
некоторая переменная (например: прогиб, внутреннее усилие,
частота, время, запас прочности и т.п.). К таким задачам относится, например, поиск параметров сечений балки, значения
274

Численные методы оптимизации
которых приводят к наилучшему совпадению заданной эпюры напряжений с расчетной, и т. п.
В этом случае использование частного критерия оптимизации сводится к замене непрерывных характеристик конечным множеством узловых точек и выбору одной из следующих целевых функций, подлежащих минимизации [20]:
p |
|
||
Z(X ) = åa j | y(X ,ω j ) − yTT (X ,ω j ) | ; |
(8.12) |
||
j=1 |
|
||
Z(X ) = max a j | y( X ,ω j ) − yTT (X ,ω j ) | ; |
(8.13) |
||
j [1:p] |
|
||
|
|
|
|
|
p |
|
|
Z(X ) = åa j [ y(X ,ω j ) − yTT (X ,ω j )]2 / n , |
(8.14) |
||
|
j=1 |
|
|
где: р – количество узловых точек ωj на оси переменной ω; аj – весовые коэффициенты, значения которых тем больше, чем
меньшее отклонение y(X , ω j ) − yTT (X , ω j ) нужно получить в j-й точке.
Максиминные (минимаксные) критерии позволяют достичь одной из целей оптимального проектирования – наилучшего удовлетворения условий работоспособности (8.8).
Введем количественную оценку степени выполнения j-го условия работоспособности, обозначим ее через vj и будем называть запасом работоспособности параметра yj. Расчет запаса по j-му выходному параметру можно выполнить различными способами [20], например,
|
|
|
æ TT |
j |
- y |
jном |
ö |
|
|
|
v |
j |
= a |
ç |
|
|
-1÷ |
, |
(8.15) |
||
|
|
|
|
|||||||
|
|
j ç |
|
d j |
|
÷ |
|
|
||
|
|
|
è |
|
|
|
ø |
|
|
|
где aj – весовой коэффициент; yj ном – номинальное значение j-го выходного параметра; δj – величина, характеризующая разброс j-гo выходного параметра.
Здесь предполагается, что все соотношения сведены к виду
275

Численные методы оптимизации
уj< ТТj.
Если уj>ТТj, то
–уj< –ТТj,.
G Рекомендуется [20] принимать: 1) aj > 1 (рекомендуемые значения 5≤ aj ≤20), если желательно достичь выполнения j -го технического требования с заданным допуском, т.е. уj= ТТj ± yj; 2) aj = 1, если необходимо получить максимально возможную оценку vj.
Качество функционирования технической системы характеризуется вектором выходных параметров и,
следовательно, вектором V = (v1, v2 ,...,vm ) . Поэтому целевую
функцию следует формировать как некоторую функцию ϕ(V )
вектора оценок. Например, если в качестве целевой функции рассматривается запас только того выходного параметра, который
в данной точке Х является наихудшим с позиций выполнения требований ТЗ, то
Z(X ) = min v j (X ) , |
(8.16) |
1≤ j≤m
где т – количество запасов работоспособности.
Естественно теперь поставить задачу о выборе такой
стратегии поиска Х , которая максимизировала бы минимальный из запасов, т.е.
max Z(X ) = max |
min v j (X ) |
(8.17) |
X Xd |
1≤ j≤m |
|
где Xd – допустимая область для поиска.
Критерий оптимизации с целевой функцией (8.17) называют
максиминным критерием.
8.2.3. Назначение ограничений
Ограничения объективно появляются при проектировании технических объектов и объектов управления и вытекают из
276

Численные методы оптимизации
конкретной физической и технологической реализуемости внутренних параметров элементов, ограниченности ресурсов и т.п.
При постановке задачи оптимизации учет ограничений иногда бывает принципиально необходим. Так, если целевая функция имеет вид Z(x) = а + bх и не наложены ограничения на параметр х, то задача поиска экстремального значения Z(x) становится некорректной. Ограничения суживают область решений, и искомый экстремум становится условным.
Различают прямые и функциональные ограничения.
Прямые ограничения имеют вид |
|
xнi ≤ xi ≤ xвi при i [1:n], |
(8.18) |
где xнi, xвi – минимально и максимально допустимые значения i-го управляемого параметра; п – размерность пространства управляемых параметров. Например, для многих объектов параметры элементов не могут быть отрицательными: xнi,> 0 (геометрические размеры, массы и т. п.).
Функциональные ограничения, как правило,
представляют собой условия работоспособности выходных параметров, не вошедших в целевую функцию.
Они представляют собой математическое описание требований, обеспечивающих функционирование
проектируемого объекта на всех этапах его существования и устанавливающих основные взаимосвязи оптимизируемых параметров [2]:
−экономические, включающие в себя ограничения ресурсов, требования к сбыту, торговле, организационной системе;
−прочностные, обеспечивающие работоспособность конструкции в целом, отдельных ее узлов из условий прочности, жесткости,
устойчивости, долговечности; условия равновесия, совместности деформаций, формула Мора для определения прогиба и т.п.;
277

Численные методы оптимизации
−конструктивно-технологические, описывающие специальные
конструктивные или технологические требования;
−геометрические, позволяющие по полученным значениям искомых
оптимизируемых параметров х1, х2, х3,….хn, а также по совокупности параметров а1, а2, …аm, заданных в качестве исходной информации, воспроизвести объект с той степенью детализации,
которая необходима исследователю при решении конкретной задачи;
−механические, описывающие кинематические и динамические характеристики объекта (взаимное расположение узлов и элементов конструкции, внешние усилия, инерционные силы, массу конструкции и т.п.).
Функциональные ограничения могут иметь вид:
1)равенств (8.2) и (или)
2)неравенств (8.3).
Прямые и функциональные ограничения формируют допустимую область поиска. Если ограничения (8.2) и (8.3) совпадают с условиями работоспособности (8.8), то допустимую
область называют также областью работоспособности.
8.2.4. Нормирование управляемых и выходных параметров
Пространство управляемых параметров – метрическое.
Поэтому при выборе направлений и величин шагов поиска следует вводить ту или иную норму, отождествляемую с расстоянием между двумя точками. Последнее предполагает, что
все управляемые параметры имеют одинаковую размерность или являются безразмерными.
Возможны различные способы нормирования. В качестве примера рассмотрим способ логарифмического нормирования,
достоинством которого является переход от абсолютных приращений параметров к относительным. В этом случае i-й управляемый параметр ui преобразуется в безразмерный xi
следующим образом [20]: |
|
xi = ln(ui ξi ) , |
(8.19) |
278

Численные методы оптимизации
где ξi – коэффициент, численно равный единице параметра ui.
Нормирование выходных параметров можно выполнить с помощью весовых коэффициентов, как в аддитивном критерии, или переходом от yj к запасам работоспособности vj по (8.15).
8.2.5. Примеры постановок задач оптимального проектирования
Теорию оптимального проектирования отличает большое разнообразие постановок задач. Минимизация веса конструкций при ограничениях по прочности, жесткости, задачи отыскания
оптимальных форм поперечных сечений элементов конструкций являются основными в теории оптимального проектирования строительных сооружений. При этом для различных типов конструктивных элементов (балки, колонны, фермы, пластинки, оболочки) уравнения связи, ограничения, а также действующие нагрузки существенно отличаются.
Рассмотрим некоторые характерные примеры построения математических моделей задач оптимального проектирования.
n Задача 8.1. Пусть требуется спроектировать прямоугольный контейнер (рис.8.5.) объемом 1 м3 для перевозки какого-то вида продукции. Желательно, чтобы на изготовление контейнера затрачивалось как можно меньше материала. При условии постоянства толщины стенок это означает, что площадь поверхности
должна быть минимальной.
Чтобы контейнер было удобно брать автопогрузчиком, его ширина должна быть не менее 1,5 м.
Составим математическую модель задачи.
Проектные параметры: х1, х2, х3 – длина, ширина и высота контейнера.
279
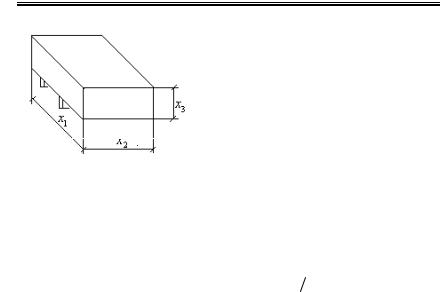
Численные методы оптимизации |
|
|
Целевая |
функция |
должна |
описывать |
площадь |
боковой |
поверхности |
контейнера |
(м2), |
которую |
требуется |
|
минимизировать:
|
Zmin = 2(x1 x2 + x2 x3 + x1 x2 ) |
(8.20) |
|
|
Ограничение - равенство (объем |
||
|
|||
Рис.8.5. Проектируемый контейнер |
контейнера (м3) |
х1 х2 х3 =1 |
(8.21) |
|
Ограничения – неравенства: |
||
|
х1 ³ 1,5; х2 ³ 0; |
х3 ³ 0. |
(8.22). |
Внимательный конструктор заметит, что ограничение – равенство, благодаря своей простоте, позволяет уменьшить размерность задачи.
Действительно, если |
выразить х3 =1 х1 х2 , |
то |
х3 можно |
|||||||||||||
исключить из проектных параметров. |
|
|
|
|
|
|||||||||||
Формулируя задачу вновь, мы будем иметь: |
|
|
||||||||||||||
Проектные параметры: х1, х2, |
|
|
1 |
|
1 |
|
|
|
||||||||
Целевая функция: |
|
Z |
min |
= 2(x x |
2 |
+ |
+ |
) |
|
(8.23) |
||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
х1 |
|
х2 |
|
|
||||
Ограничений - равенств |
нет; |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||
Ограничения - неравенства: |
|
х1 ³1,5; х2 ³ 0. |
|
(8.24) |
||||||||||||
Целевая функция и ограничения задачи - нелинейны, |
||||||||||||||||
следовательно, |
мы |
|
|
|
получили |
задачу |
нелинейного |
|||||||||
программирования. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если воспользоваться обычным определением минимума и |
||||||||||||||||
принять |
¶Z |
= 0; |
|
¶Z |
= 0, то |
|
будет получен |
результат: |
||||||||
|
|
|
||||||||||||||
|
¶x |
|
¶x |
2 |
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
х1=х2=х3=1м. Однако при таком решении не удовлетворено ограничение - неравенство, и следовательно, такое решение неприемлемо, т.е. требуется другой подход к решению данной задачи, которое мы получим позднее при рассмотрении методов решения задач нелинейного программирования.
280

Численные методы оптимизации
Если при проектировании контейнера поставить другую цель – сделать минимальным объем сварочных работ, т.е.
получить минимальную длину сварочных швов, то целевая функция будет иметь вид:
Z(min)= 4 (x1 + x2 + x3) |
(8.25) |
и соответственно решение задачи будет иным.
Вообще, выбор целевой функции носит субъективный характер, и поэтому объект может быть оптимален только в смысле данного критерия.
n Задача 8.2. Требуется спроектировать произвольную ферму (в общем случае – статически неопределимую), имеющую минимальный
теоретический вес при действии на нее нескольких несовместимых
(взаимоисключающих) нагрузок.
Пусть n число стержней фермы; m – число лишних стержней; t – число несовместимых нагрузок.
Целевую функцию – теоретический вес фермы можно записать [10] как
n |
|
Zmin = åci Fi . |
(8.26) |
i=1
Обозначим Sik – усилие в i-м стержне от k-й нагрузки. Усилия в m
лишних стержнях принимаем за лишние неизвестные в основной системе метода сил.
Тогда уравнения связи (ограничения – равенства) в задаче оптимизации можно записать в виде [11]
|
m |
|
|
Sik |
= NikP + åN ij S jk |
(i=1,2,…,n), |
(8.27) |
|
j=1 |
|
|
где NikP и N ik – |
усилия в i -м стержне от k-й нагрузки и от |
||
единичного усилия Хj =1 в основной системе метода сил. |
|
||
281

Численные методы оптимизации
Введем в рассмотрение вспомогательные переменные особого рода "запасы площадей сечений стержней по растяжению и сжатию" [10]:
u |
ik |
= F - |
Sik |
|
, |
(8.28) |
||
|
||||||||
|
i |
s |
|
|
|
|||
|
|
|
|
|
|
|
||
v |
ik |
= F + |
Sik |
|
, |
(8.29) |
||
|
|
|||||||
|
i |
sji |
|
|
|
|||
|
|
|
|
|
|
|
||
где Fi – площадь поперечного сечения стержня; ji – коэффициенты продольного изгиба.
GЗамечание. Величины "запасов системы" могут быть полезны при расчете и других оптимальных систем.
Вкачестве проектных параметров принимаем площади поперечных сечений Fi и запасы по растяжению uik и сжатию vik .
Впрочной системе эти параметры должны быть неотрицательны.
И еще одна группа ограничений – неравенств: |
|
Fi ³ 0; uik ³ 0; vik ³ 0. |
(8.30) |
Выразим усилия через площади и запасы по растяжению:
|
Sik |
|
= F - u |
ik |
. |
|
|
|
||
|
|
|
|
|
|
|||||
|
s |
|
i |
|
|
|
|
|
||
Подставляя это выражение в (8.27) и (8.29), получим |
|
|||||||||
m |
|
|
|
|
|
1 |
|
|
||
Fi - uik - åN ij (Fj - u jk |
) = |
NikP , |
(8.31) |
|||||||
s |
||||||||||
j=1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
Fi (ji +1) - uik |
- ji vik |
= 0 |
|
|
(8.32) |
|||||
(i=1,2,…,n; k=1,2,…,t).
Теперь задача сводится к минимизации целевой функции
(8.26) при условиях (8.31) и (8.32) и требованиях (8.30).
Эта задача записана в стандартной форме задачи линейного программирования. Эта постановка отличается тем, что допускает
282
