
Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ
.pdf
Численные методы решения дифференциальных уравнений
Обозначим величину зависимой переменной f(x,y).
По аналогии с обыкновенными производными частную производную f(x,y) принято представлять в виде (центрально- разностная формула производной от f по x при постоянном y)
∂f |
≈ |
f (xi + h, y j ) − f (xi − h, y j ) |
. |
(6.64) |
|||
∂x |
2h |
|
|||||
|
|
|
|
|
|||
Аналогично можно записать производную от f по y при |
|||||||
постоянном x: |
|
|
|
|
|
|
|
∂f |
≈ |
|
f (xi , y j + k) − f (xi , y j − k) |
. |
|
(6.65) |
|
∂y |
|
|
2k |
|
|||
|
|
|
|
|
|
||
Здесь также можно использовать левые и правые разности. Шаг по осям x и y может быть принят и одинаковым, например h.
Для удобства обозначения f (xi + h, y j ) заменим на fi+1, j , а f (xi , y j + k) на fi, j+1 и т.п.
Тогда, выражения для частных производных первого и второго порядка в узле c координатами xi и yj можно записать:
|
|
|
∂f |
≈ |
fi+1, j − fi−1, j |
|
; |
|
|
∂f |
≈ |
fi, j+1 − fi, j−1 |
; |
|
(6.66) |
||||||
|
|
|
∂x |
|
2h |
|
|
∂y |
|
2k |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∂2 f |
≈ |
fi+1, j − 2 fi, j |
+ fi−1, j |
|
; |
∂2 f |
≈ |
fi, j+1 |
− 2 fi, j |
+ fi, j−1 |
. |
(6.67) |
|||||||||
∂x2 |
|
|
|
|
|
h2 |
|
|
|
∂y2 |
|
|
|
k 2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Смешанная производная |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
∂2 f |
|
≈ |
fi+1, j+1 − fi−1, j+1 − fi+1, j−1 |
+ fi−1, j−1 |
. |
|
|
|
(6.68) |
|||||||||
|
|
|
∂x∂y |
|
|
|
|
|
4hk |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Далее дифференциальные операторы в определяющем уравнении задачи заменяют их разностными аналогами. При этом решаемое
уравнение в частных производных записывают в наиболее удобной системе координат и, представляя производные в конечно-
183
Численные методы решения дифференциальных уравнений
разностной форме, приводят его к виду разностного уравнения.
Полученное разностное уравнение используют в дальнейшем для описания связи между соседними узлами сетки. Разностное уравнение записывают для всех внутренних узлов сетки. При
переходе от дифференциальной задачи к разностной необходимо также аппроксимировать граничные условия. Совокупность
разностного уравнения и разностных краевых условий называется
разностной схемой краевой задачи, которая представляет собой систему n уравнений с n неизвестными значениями искомой функции в узлах.
Полученную систему алгебраических уравнений решают одним из численных методов (см. главу 2).
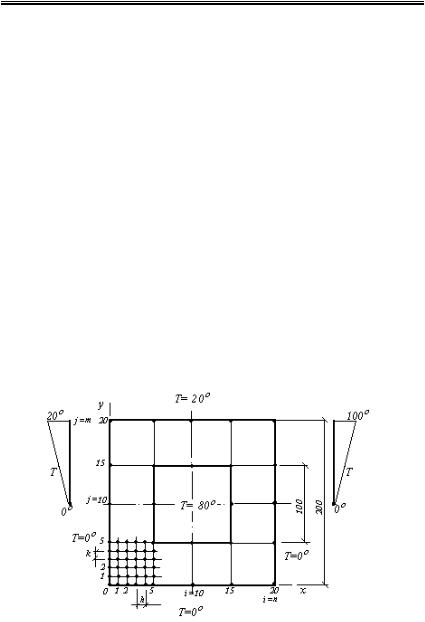
n Пример 6.12. Рассмотрим длинную квадратную трубу с квадратным отверстием, по которой течет горячая жидкость. Труба наполовину погружена в ледяную ванну, так что температура нижней половины поверхности трубы равна 0оС. Верхняя плоскость трубы находится при постоянной температуре 20оС. Кроме того, предположим, что температура наружной поверхности трубы линейно изменяется от 0оС до 20оС на участке между ледяной ванной и верхней плоскостью трубы. Жидкость внутри трубы имеет температуру 80 оС. Наружный размер трубы равен 200 мм, внутренний – 100 мм. Поперечное сечение трубы изображено на рис.6.14.
Рис.6.14. Сечение трубы в примере 6.12
184

Численные методы решения дифференциальных уравнений
Распределение температуры в теле трубы удовлетворяет уравнению в частных производных
∂2Т |
+ |
∂2Т |
= а |
∂Т |
, |
(6.69) |
∂x2 |
|
∂y2 |
|
∂t |
|
|
где постоянная а учитывает теплоемкость, теплопроводность и плотность материала трубы.
В этой задаче будем считать, что жидкость течет достаточно долго, чтобы все переходные процессы успели закончиться, т.е. тепловой режим
трубы стал стационарным. |
Тогда |
∂Т |
= 0 и |
уравнение приобретает |
|||
∂t |
|||||||
следующий вид: |
|
|
|
|
|
||
|
|
|
|
|
|
||
∂2Т |
+ |
∂2Т |
= 0 . |
|
(6.70) |
||
∂x2 |
|
∂y2 |
|
|
|
|
|
Этому уравнению удовлетворяет распределение температур внутри трубы, а распределение температур на границах трубы задано граничными условиями:
T=f(x,y). |
(6.71) |
Таким образом, наша задача представляет собой краевую задачу
Дирихле для уравнения Лапласа.
Нанесем на сечение трубы сетку, разделив ее в направлении х на n интервалов каждый, размером h, а в направлении у – на m интервалов каждый, размером k .Порядок нумерации узлов показан на рис. 6.14.
.Начало координат совпадает с точкой 0,0.
Заменим частные производные в уравнении (6.70) их разностными аналогами в соответствии с формулами (6.66):
|
Ti+1, j − 2Ti, j +Ti−1, j |
+ |
Ti, j−1 − 2Ti, j +Ti, j+1 |
= 0 . |
(6.72) |
|
|
|
|
||||
|
h2 |
k 2 |
|
|||
Если обозначить |
λ = k h , |
то дифференциальное |
уравнение |
|||
сведется к разностному уравнению |
|
|
|
|||
λ2Ti+1, j + λ2Ti−1, j |
+Ti, j+1 +Ti, j−1 − 2(1+ λ2 )Ti, j = 0 |
(6.73) |
||||
|
для i=1,2,3,…,n–1 и j=1,2,3,…,m–1. |
|
||||
185

Численные методы решения дифференциальных уравнений
Этому уравнению удовлетворяет распределение температур внутри трубы, а распределение температур на границах задается граничными условиями.
Пусть h=k, т.е. интервалы разбиения в направлениях х и у примем одинаковыми, тогда λ=1 и разностные уравнения можно записатькак
|
4Ti, j −Ti+1, j −Ti−1, j −Ti, j+1 −Ti, j−1 |
= 0 |
(6.74) |
|
для i=1,2,3,…,n–1 и j=1,2,3,…,m–1. |
|
|
Предположим, что по наружному размеру в направлениях х и у |
|||
сделано разбиение на 20 интервалов, так что h=k=10 мм. |
|
||
Тогда граничные условия запишутся так: |
|
|
|
Ti,0=0, |
i=0,1,…,20. |
|
|
Ti,20=20, |
i=0,1,…,20. |
|
|
Ti,5= Ti,15=80, |
i=5,6,…,15. |
(120 уравнений) |
(6.75) |
T5,j= T15,j=80, |
j=6,7,…,14. |
|
|
|
|
ì0, |
|
j=1,2,…10, |
|
T0, j |
= T20, j |
ï |
|
|
|
= í20 |
( j -10), |
j=11,12,…19. |
|||
|
|
ï |
|
||
|
|
|
|||
|
|
î10 |
|
|
|
Запишем подробнее несколько разностных уравнений (6.74):
При |
j =1 |
−T2,1 −T1,2 |
= Т |
|
+Т |
|
|
|
|
|||
i=1 |
4T1,1 |
0,1 |
1,0 |
, |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
i=2 |
−T1,1 |
+ 4T2,1 −T3,1 −T2,2 = |
Т |
2,0 |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
……………………………..
i=19 |
−T18,1 + 4T19,1 −T19,2 = Т |
19,0 |
+Т |
20,1 |
. |
(6.76) |
|||
|
|
|
|
|
|
|
|||
При |
j =2 |
|
|
|
(240 уравнений) |
||||
|
|
|
|
|
|
||||
i=1 |
−T1,1 + 4T1,2 −T2,2 −T1,3 = Т |
0,2 |
, |
|
|
|
|||
i=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
−T2,1 −T1,2 + 4T2,2 −T3,2 −Т2,3 |
= 0 , |
|
|||||||
i=19 |
…………………………….. |
|
. |
|
|||||
−T19,1 −T18,2 + 4T19,2 −Т19,3 |
= Т |
20,2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
……………………………..
Продолжая и далее таким же образом, т.е. увеличивая каждый раз j и проходя значения i=1,2,…,19 до j=19, получим систему 240 линейных
186

Численные методы решения дифференциальных уравнений
алгебраических уравнений. Дополнив ее граничными условиями (6.75), окончательно имеем систему уравнений относительно 360 неизвестных. Эта СЛАУ обладает двумя важными свойствами, которые помогут выбрать для нее метод решения.
Свойства эти следующие:
1.Система разреженная, т.е. подавляющая часть коэффициентов равна нулю.
2.В каждом уравнении один из коэффициентов равен 4, сумма же остальных коэффициентов меньше или равна 4 по модулю.
Таким образом, в этой системе выполнены условия сходимости
итерационного метода и наиболее рациональным методом решения полученной системы уравнений является метод Гаусса – Зейделя.
Метод Гаусса – Зейделя в применении к эллиптическим
разностным уравнениям называется методом Либмана или
методом последовательных смещений [26].
Итерационный процесс по полученным формулам (6.75), (6.76) продолжают до тех пор, пока для двух соседних итераций n и n+1 не будет выполняться условие:

 T n+1 − T n
T n+1 − T n 
 ≤ ε ,
≤ ε ,
где ε > 0 – заданная погрешность.
В данном примере рассмотрено уравнение Лапласа. Вообще говоря, любое эллиптическое уравнение без членов, содержащих смешанную производную, приводит к системе разностных уравнений, удовлетворяющей условиям сходимости.
Существуют и другие способы решения разностных уравнений (6.75) – (6.76). Наиболее часто используются методы
линейной релаксации, блочной релаксации и метод чередующихся направлений [25]. Часто они оказываются более эффективными, нежели метод Либмана.
Сходимость метода конечных разностей
При использовании приближенных методов очень важным является вопрос о сходимости.
187
Численные методы решения дифференциальных уравнений |
|||||
Понятие сходимости может быть сформулировано по- |
|||||
разному. Ранее отмечалось, что при h→0 и k→0 разностное |
|||||
уравнение приближается к дифференциальному уравнению. |
|||||
Однако при решении практических задач нас обычно интересует |
|||||
другой вопрос: приближается ли при h→0 и k→0 решение |
|||||
разностного уравнения к решению дифференциального уравнения? |
|||||
Для эллиптических уравнений на этот вопрос можно дать |
|||||
положительный ответ, хотя мы и не будем воспроизводить здесь |
|||||
доказательство. |
|
|
|
|
|
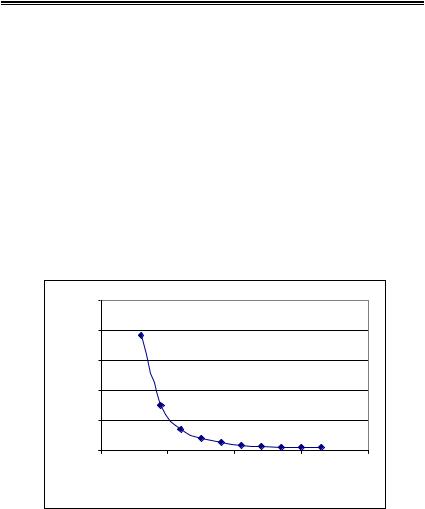
В частности, для примера 6.12. с увеличением числа |
|||||
разбиений норма разности двух решений стремится к нулю, т.е. |
|||||
разностная задача сходится к точному решению (см. рис.6.15). Для |
|||||
относительной погрешности ε=0,001 карта изотерм (линий |
|||||
постоянной температуры) приведена на рис.6.16. |
|
||||
ε |
2,5 |
|
|
|
|
|
2 |
|
|
|
|
|
1,5 |
|
|
|
|
|
1 |
|
|
|
|
|
0,5 |
|
|
|
|
|
0 |
|
|
|
N |
|
|
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
Рис.6.15. Сходимость разностной задачи (в зависимости от числа |
|||||
|
|
|
разбиений N) |
|
|
188

Численные методы решения дифференциальных уравнений
Рис.6.16. Карта изотерм для трубы из примера 6.12.
В случае параболических и гиперболических уравнений требуется соблюдать некоторые ограничения, которые обеспечили бы такого рода сходимость [25].
Для гиперболических уравнений достаточным, но не необходимым условием сходимости является условие k< h , а для
параболических k < |
h2 |
, т.е. здесь накладываются довольно |
|
||
2 |
|
|
серьезные ограничения на выбор шага k по времени.
189

Численные методы решения дифференциальных уравнений
На практике оценка сходимости разностной схемы, как и в задачах Коши, производится методом половинного шага, т.е. находится численное решение задачи на сетке Ωn с шагом h и на сетке Ω2n с шагом h/2. Если значения полученных решений (двух сеточных функций) в одинаковых узлах отличаются друг от друга не более чем на 1-5%, то полученную сеточную функцию на сетке Ω2n принимают за приближенное решение задачи. В противном случае шаг уменьшают еще в два раза. Понятие сходимости
разностной схемы тесно связано с понятием точности и устойчивости.
Точность аппроксимации и устойчивость решения можно оценить следующим образом. Известно, что ошибка, возникающая при замене производных конечными разностями, пропорциональна квадрату шага h2 (т.е. ~ch2 ). Производя расчет на двух, трех сетках с различными шагами h , сравнивают решения. Если при убывании h все решения близки между собой и стремятся к некоторому пределу со скоростью, соответствующей порядку c(h2) точности схемы, то это свидетельствует о хорошей сходимости и устойчивости.
6.5. Вариационный подход к решению краевых задач
Вариационный подход – это применение вариационных методов к решению краевых задач. Он получил широкое распространение после того, как немецкий математик Ритц в 1908
году предложил удобный прием построения приближенного решения вариационной задачи.
Прежде чем рассматривать вариационные методы решения краевых задач, введем некоторые основные понятия теории вариационного исчисления.
6.5.1. Основные понятия вариационного исчисления
Основным объектом изучения вариационного исчисления является функционал [46].
190

Численные методы решения дифференциальных уравнений
Функционал – это функция, зависящая от функции, т.е.
аргументом функционала является функция. Примером
функционала может служить определенный интеграл J = òb f (x)dx ,
a
который принимает некоторое числовое значение при подстановке каждой конкретной функции в подынтегральное выражение.
Функционал может зависеть от нескольких функций или от функций нескольких независимых переменных.
В вариационном исчислении изучаются методы нахождения экстремальных значений функционалов. Задачи, в
которых требуется исследовать функционал на максимум или минимум, называются вариационными задачами.
Методы решения вариационных задач весьма сходны с методами исследования функций на максимум или минимум.
В дифференциальном исчислении [9, 28] рассматривается
доказательство теоремы:
Если дифференцируемая функция f(x) достигает максимума или минимума во внутренней точке x=x0 области определения функции, то в этой точке df = 0 .
Следовательно, для нахождения экстремума функции, вычисляется 1-я производная этой функции и приравнивается к нулю. В результате определяется значение аргумента х0, при котором функция f максимальна или минимальна.
При исследовании функционалов вариация функционала δJ играет такую же роль, как и дифференциал df при исследовании функций.
В вариационном исчислении [46] доказывается аналогичная теорема:
Если функционал J[ y(x)] , имеющий вариацию, достигает максимума или минимума при y=y0(x), где y(x) – внутренняя точка области определения функционала, то при y=y0(x) δJ = 0 .
191

Численные методы решения дифференциальных уравнений
Значит, необходимым условием экстремума функционала является обращение в нуль вариации функционала. Процесс
варьирования функционалов производится аналогично дифференцированию сложных функций.
Поскольку аргументом функционала является функция, то именно функция y=y0(x), которая называется эстремалью, доставляет экстремум функционалу.
Отметим, что если y(x) доставляет функционалу J минимум, тоδ 2J ³ 0 , а если максимум , то δ 2 J ≤ 0.
6.5.2. Связь решения краевой задачи с нахождением минимума функционала
Многие законы механики и физики сводятся к утверждению, что некоторый функционал, связанный с физическим процессом, должен достигать минимального или максимального значения. В
такой формулировке эти законы называются вариационными принципами механики или физики.
Например, вариационный принцип возможных перемещений
Лагранжа формулируется так
Из всех возможных перемещений упругой системы, только
действительные перемещения сообщают полной потенциальной энергии минимальное значение,
или упругая система находится в равновесии, если сумма работ всех
внешних и внутренних сил на любых возможных перемещениях равна 0.
Аналитически это можно записать δП = δ(U −Т ) = 0 .
Здесь: П – полная потенциальная энергия системы (функционал),
U – потенциальная энергия упругой деформации, Т – работа внешних сил.
В вариационном исчислении [46] рассматривается доказательство того, что если функция y = y(x) доставляет
192
