Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ

.pdf

Скачиваний:

333

Добавлен:

29.03.2015

Размер:

2.5 Mб

Скачать

☆

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 3518 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Численные методы решения дифференциальных уравнений

Степень точности метода оценивается с помощью алгоритма

половинного шага, описанного выше.

Реализация данного метода с использованием таблиц Microsoft Excel приведена в подразделе 6.6.2.

6.4. Численные методы решения краевых задач

Точное решение краевых задач удается получить лишь для немногих частных случаев. Поэтому общий способ их решения заключается в использовании различных приближенных методов.

В настоящее время наиболее широкое распространение получили численные методы, в основе которых лежит метод сеток.

Сущность метода сеток состоит в аппроксимации искомой непрерывной функции совокупностью приближенных значений, рассчитанных в некоторых точках области – узлах. Совокупность узлов, соединенных определенным образом, образует сетку. Сетка,

в свою очередь, является дискретной моделью области определения искомой функции.

Применение метода сеток позволяет свести дифференциальную краевую задачу к системе алгебраических (линейных или нелинейных) уравнений относительно неизвестных узловых значений функций.

Наиболее часто на практике используются два метода сеток:

1)метод конечных разностей (МКР);

2)метод конечных элементов (МКЭ) (глава 7).

Воснове МКР лежит конечно-разностная аппроксимация

производных в определяющих уравнениях задачи.

Воснове МКЭ лежит вариационный подход, т.е. решение основной вариационной задачи – исследование экстремума функционала, связанного с физической сущностью задачи.

Существуют и другие подходы к построению численного решения краевых задач, например, переход от исходного

дифференциального уравнения в частных производных к

173

Численные методы решения дифференциальных уравнений

эквивалентному интегральному уравнению, подлежащему дальнейшим преобразованиям. Примером указанного подхода служит метод интегральных граничных элементов (МГЭ) [20],

который в данном пособии не рассматривается.

Численные методы можно применять только к корректно поставленным задачам. Задача считается корректной, если для нее

существует решение, оно единственно и непрерывно зависит от входных данных. Таким образом, численное решение задачи считается корректным, если ее дискретный аналог сохраняет свойства корректности, т.е. получаемая система алгебраических

уравнений имеет единственное решение и оно устойчиво к входным данным (коэффициентам дифференциального уравнения, начальным или граничным условиям).

Если поведение конструкции или явления описывается единственным дифференциальным уравнением, то приближенное решение можно получить как методом конечных элементов, так и методом конечных разностей. Если же конструкция в целом

неоднородна и состоит из большого числа отдельных конструктивных элементов, поведение каждого из которых описывается своим дифференциальным уравнением, то в этом случае, как правило, применяют метод конечных элементов или метод граничных элементов.

6.4.1 Метод конечных разностей решения краевых задач

Метод конечных разностей является универсальным и наиболее распространенным численным методом решения краевой задачи. При реализации МКР:

§Область непрерывного аргумента заменяется дискретным множеством точек, разностной сеткой Ωn (6.43).

§Искомая непрерывная функция заменяется сеточной функцией, для чего все производные, входящие в дифференциальное уравнение, и краевые условия заменяются конечно- разностными аналогами, выраженными через значения искомой

174

Численные методы решения дифференциальных уравнений

функций в узлах сетки. Этот процесс называется конечно-

разностной аппроксимацией (КРА).

§В результате КРА краевая задача заменяется системой линейных алгебраических уравнений, решение которой дает значения сеточной функции yi.

Конечно-разностная аппроксимация для функций одной

переменной

Конечно-разностная аппроксимация – основное понятие теории разностных схем. Это наиболее распространенный прием численного интегрирования как обыкновенных, так и дифференциальных уравнений в частных производных.

Начнем с КРА функций одной переменной.

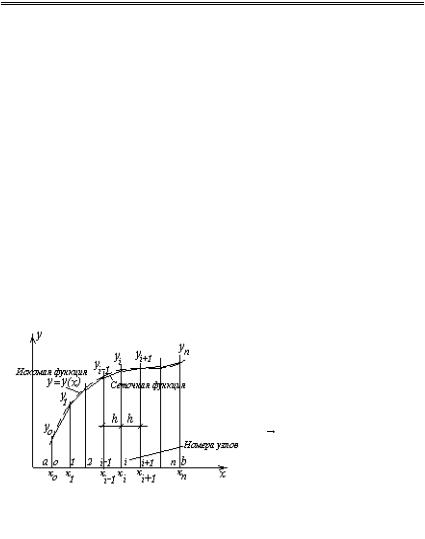
Рассмотрим функцию y = y(x), непрерывную на отрезке [a,b]. На область непрерывного аргумента x нанесем разностную сетку

Ωn (6.43) (рис.6.8).

Функцию непрерывного

аргумента		y=y(x)
заменим		функцией
дискретного		аргумента
на	данной	сетке
сеточной		функцией
Y{y0 , y1 ,.., yn },		где

yi=y(xi), i=0,1,..,n.

Рис.6.8. КРА функции одной

переменной

Производная функции y= y(x), по определению, есть предел

отношения приращения функции	y к приращению аргумента x
при x → 0 :	y .
y/ = lim	y .
x→0	x

175

Численные методы решения дифференциальных уравнений

В численных расчетах с достаточной степенью точности для

малых значений x можно принять
y / ≈	y	.

	x
Рассмотрим аппроксимацию производной функции y = y(x)
для сетки с постоянным шагом h, т.е. полагаем x ≈ h .
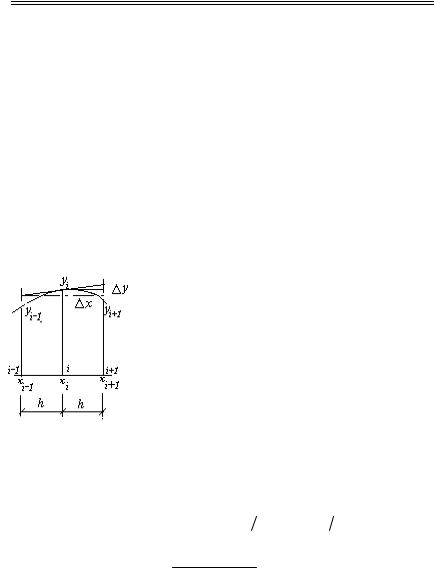
Геометрический смысл производной – тангенс угла наклона
касательной в точке (рис. 6.9).

Запишем выражения для первой производной функции в точке xi. В зависимости от способа вычисления конечных разностей

получаются разные формулы для вычисления производной в одной

и той же точке, а именно:
		y'	=		yi+1 − yi−1		–	(6.50)
		y'	=				–	(6.50)
		i				2h
						2h
		центральная разностная формула,
			y'	=		yi − yi−1	–	(6.51)
			y'	=			–	(6.51)
			i			h
						h
		левая разностная формула,

	Рис.6.9 Аппроскимация		y'	=		yi+1 − yi	–	(6.52)
	производной функции					yi+1 − yi

			i			h
						h
		правая разностная формула.
		правая разностная формула.

Можно найти также выражения для старших производных:

− y/

− y ) h − (y − y

) h

= (y

)

≈

i+1

i i−1

(6.53)

= yi−1 − 2yi + yi+1 . h2

Аналогично определяются производные высших порядков в конечных разностях.

176

Численные методы решения дифференциальных уравнений

Разностная схема краевой задачи для обыкновенного дифференциального уравнения 2-го порядка

Рассмотрим линейное дифференциальное уравнение 2-го

порядка:

y// + p(x)y/ + q(x) y = f (x)

(6.54)

с линейными краевыми условиями:

a0 y(a) + a1 y' (a) = A,

(6.55)

b0 y(b) + b1 y' (b) = B,

где

p(x), q(x), f(x) – непрерывные на [a,b] функции;

a0 , a1 , A, b0 , b1 , B

– заданные

числа, не равные

нулю

одновременно, причем

¹ 0,

¹ 0 .

Краевые условия (6.55) в общем случае задают линейную

связь между значением искомого решения и его производной на концах отрезка [a,b] в отдельности.

В частном случае, если a1 = b1 = 0 , то на концах отрезка

[a,b] задано значение искомого решения. Такое краевое условие является краевым условием I рода.

Если a0 = b0 = 0 , то на концах отрезка заданы значения производной решения. Это краевое условие II рода.

Вобщем случае, когда a j ¹ 0 , b j ¹ 0 , условие называются

краевым условием III рода.

Вотличие от имеющей всегда единственное решение задачи Коши, в которой только на одном конце задаются условия для искомой функции и ее производной, краевая задача (6.54), (6.55)

может иметь или одно решение, или бесконечное множество решений, или, наконец, может совсем не иметь решений. Не акцентируя внимание на этой проблеме, будем считать, что линейная краевая задача (6.54), (6.55) имеет единственное решение,

177

Численные методы решения дифференциальных уравнений

непрерывное на отрезке [a,b] вместе с производными до 2-го порядка включительно.

Область изменения аргумента x [a, b] заменяем разностной сеткой (дискретной сеточной областью) Ωn, (6.43), (рис.6.8).

и вводим обозначения:

pi = p(xi ),	qi = q(xi ),	fi = f (xi ),
yi = y(xi ),	yi' = y' (xi ),	yi'' = y'' (xi ), (i = 0,1,...,n).

Конечно-разностные выражения (6.50) – (6.53) подставляем в дифференциальное уравнение (6.54) и краевые условия (6.55). При этом во внутренних узлах сетки производные y', y" заменяем их конечно-разностными отношениями (6.50), (6.53), а в граничных точках x0 = a, xn = b , чтобы не выходить за пределы отрезка [a,b],

соответственно

y0' =	y1 − y0	,	yn' =	yn − yn−1	.
	h
				h

В результате этого решение краевой задачи сведено к решению системы линейных алгебраических уравнений относительно (n+1) неизвестных y0 , y1 ,..., yn .

yi−1 − 2yi

+ yi+1

+ pi

yi+1 − yi−1

+ qi yi = fi ,

(i =1,2,....,n −1),

y1 − y0

α0 y0

+ α1

= A,

(6.56)

+ β

yn − yn−1

= B.

Переход от краевой задачи (6.54) – (6.55) к системе линейных алгебраических уравнений (6.56) – есть аппроксимация краевой задачи, в которой искомой является сеточная функция

Y{y0 , y1 ,.., yn } на сетке Ωn . При этом полученная краевая задача

178

Численные методы решения дифференциальных уравнений

(6.56) называется разностной схемой для дифференциальной задачи.

После соответствующих преобразований систему (6.56)

можно привести к виду

b0 y0 + c0 y1 = A,

i =1,2,..,n −1 ,

yi−1 + bi

yi + ci yi+1 = fi ,

(6.57)

an yn−1 + bn yn = B,

где

−

= qi

−

, ci =

i =1,2,..,n −1,

(6.58)

α0 h − α1

c0 =

α1

an = −

β1

β0h + β1

(6.59)

В матричной форме система (6.57) имеет вид

A×

= D,

(6.60)

где

éb0		c0
êa	1	b	c	1
ê	1	1		1
ê		a2	b2		c2
A = ê
êK		K	K		K
ê			an−1		bn−1
ê			an−1		bn−1
ê					a	n
ë						n

ú,

K ú cn−1 úú

bn úû

é		A	ù
ê		f1	ú
ê		f1	ú
ê		f 2	ú	_
= ê	K		ú, Y
ê	K		ú
ê f		n−1	ú
ê		n−1	ú
ê		B	ú
ë			û

é	y0			ù
ê		y1		ú
ê		y1		ú
ê	y2			ú
= ê	K			ú.	(6.61)
ê	K			ú	(6.61)
ê y		n−1		ú
ê		n−1		ú
ê	y		n	ú
ë			n	û

a b c

Матрица А системы (6.57) является трехдиагональной. Система решается методом прогонки (см. подраздел 2.2.3)

относительно неизвестных y0, y1,..., yn−1, yn , т.е. значений искомой функции y=y(x) в узлах равномерной сетки заданного отрезка [a,b].

179

Численные методы решения дифференциальных уравнений

nПример 6.11. Методом конечных разностей найти решение краевой задачи.

y” +(1+x2) y = -1,

y(0) = 0,	(6.62)
y/(1) = 0.

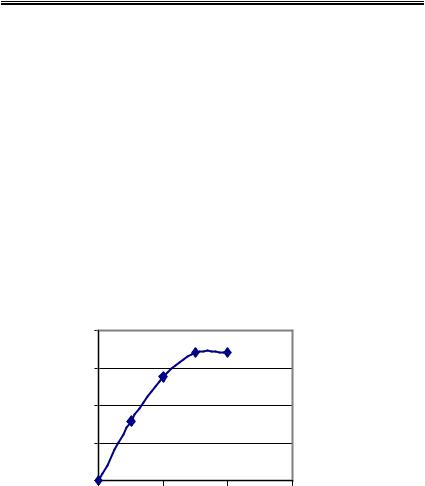
Рис.6.10. К примеру 6.11

Данная краевая задача представляет собой дифференциальное уравнение для изгибающего момента балки с переменным поперечным сечением и шарнирно закрепленным левым и жестко заделанным правым концами (рис. 6.10).

Для грубого решения построим сеточную область с шагом h = 0,25:

Ω5{0; 0,25; 0,5; 0,75; 1}.

Введем обозначения:

y0 =y(0); y1 =y(0,25); y2=y(0,5); y3=y(0,75); y4=y(1).

Таким образом, нужно определить пять значений неизвестной функции:

y0 , y1 , y2 , y3, y4 Используя конечноразностные отношения (6.50) – (6.53)

запишем

для i=0 (х =0)	y0 = 0 ,
для i=1 (х =0,25)	y0	− 2y1 + y2			+ (1+ 0,252 )y	= −1 ,

		0,252		1

для i=2 (х =0,5)	y1 − 2y2 + y3				+ (1+ 0,52)y2 = −1 ,

		0,252
для i=3 (х =0,75)	y2	− 2y3 + y4			+ (1+ 0,752 )y	= −1 ,

		0,252		3

для i=4 (х =1)	y4	− y3	= 0 .
	0,25

После подстановки в систему (6.57) и приведения подобных

систему пяти линейных алгебраических уравнений с пятью неизвестными можно записать:

180

Численные методы решения дифференциальных уравнений

é 1		0	0	0	0	ù
ê		- 30,94	16	0	0	ú
ê16						ú
ê	0	16	- 30,75	16	0	ú´
ê	0	0	16	- 30,43	16	ú
ê						ú
ê	0	0	0	- 4	4	ú
ë						û

é y0 ù êê y1 úú êê y2 úú = ê y3 ú êë y4 úû

é 0 ù êê-1úú ê-1ú

ê ú (6.63)

ê-1ú êë 0 úû

Результат решения системы уравнений, соответствующий приближенному решению краевой задачи, можно записать в виде таб.6.1.

					Таблица 6.1

xi	0	0,25	0,5	0,75	1
уi	0	0,319	0,555	0,684	0,684

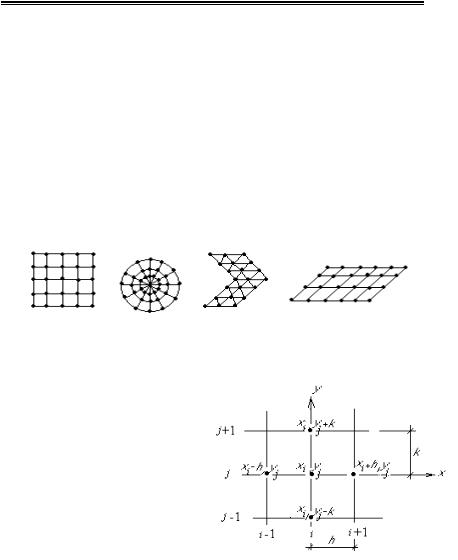
Или представить в виде графика (рис.6.11).

0,8	y	0,6840,684
0,6		0,555
0,6
0,4	0,319
0,4

0,2

		х
		х

0,5	1	1,5

Рис. 6.11. График изменения изгибающего момента по длине балки

В подразделе 6.6.3 решение этой задачи с использованием электронных таблиц Excel приведено для двух сеточных областей

(h=0,25 и h=0,125).

181

Численные методы решения дифференциальных уравнений

Конечно-разностная аппроксимация функций двух

переменных

Конечно-разностная аппроксимация для частных

производных во многом напоминает рассмотренную выше для

обыкновенных дифференциальных уравнений.

В область решения вводят равномерную сетку «узловых точек», соответствующую характеру задачи и граничным условиям. Виды сеток, наиболее часто используемых при

численном решении дифференциальных уравнений в частных производных, показаны на рис.6.12. Обычно в МКР используют правильные (регулярные) сетки, шаг которых либо одинаковый по осям х и у, либо разный.

Рис. 6.12 Виды сеток: а – прямоугольная; б – полярная; в – треугольная;

г– скошеная

Вслучае двух независимых переменных х и

уобласть является двухмерной. Она покрывается

сеткой прямоугольных клеток шириной h в направлении ОХ и высотой k в направлении

ОУ.

Пусть какая-то точка

прямоугольной сетки имеет координаты xi,yj.

Рис. 6.13. Фрагмент сетки

Индекс i присваивается переменной x, а индекс j – переменной y.

182

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 3518 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Соседние файлы в папке Информатика 2 сессия

#
29.03.201513.23 Кб87литература.docx
#
29.03.2015860.79 Кб125Раздел1.Решение нелинейных уравнений.docx
#
29.03.2015354.02 Кб87Раздел2.Методы численного интегрирования.docx
#
29.03.2015572.5 Кб113Раздел3.Решение СЛАУ.docx
#
29.03.201572.69 Кб88Раздел4.Задания.docx
#
29.03.20152.5 Mб333Численные методы решения задач строительства на ЭВМ.pdf