
Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ
.pdf
Аппроксимация
L (4) = 1× |
(4 - 2)(4 - 3)(4 - 5) |
+ 5× |
(4 -1)(4 - 3)(4 - 5) |
+14 |
× |
(4 -1)(4 - 2)(4 - 5) |
+ |
||||
|
|
|
|
||||||||
3 |
(1 |
- 2)(1 |
- 3)(1- 5) |
|
(2 -1)(2 - 3)(2 - 5) |
|
(3 -1)(3 - 2)(3 - 5) |
|
|||
|
|
|
|
||||||||
|
|
|
+ 81× |
(4 -1)(4 - 2)(4 - 3) |
= 43. |
|
|
|
|||
|
|
|
(5 -1)(5 - 2)(5 - 3) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Далее, при изучении метода конечных элементов мы еще обратимся к интерполяционным полиномам Лагранжа.
Известны и другие формулы интерполяции, например,
интерполяционная формула Ньютона [9, 12], применяемая при
интерполяции в случае равноотстоящих узлов или интерполяционный полином Эрмита [9].
4.2.3. Интерполяционный полином Эрмита
При решении некоторых практических задач (например, в методе конечных элементов) более целесообразно бывает
использовать в качестве узловых параметров не только значения самой функции, но и значения ее производных. Т.е.
интерполяционный полином должен удовлетворять условиям непрерывности, как самой функции, так и ее производных до порядка т-1 включительно (где т-порядок полинома) В этом
случае в качестве аппроксимирующих полиномов вместо полиномов Лагранжа используют полиномы Эрмита.
Рассмотрим задачу интерполирования функции y=f(x) в общей постановке. Пусть функция y=f(x) задана в n узлах отрезка [a, b ] и пусть в этих же точках известны производные этой функции, т.е. на отрезке [a, b] заданы:
Значения: |
y , y' |
в узле x1, |
|
|
|
1 |
1 |
|
|
……………………………………… |
(4.9) |
|||
Значения: |
yn , yn' |
в узле xn, |
|
|
Задача ставится следующим образом: построить многочлен H(x) максимальной степени 2n-1, такой, при котором
H (xi ) = yi ; |
H ' (xi ) = yi' , i =1,2,..,n. |
(4.10) |
123

Аппроксимация
Если все xi различны, то существует единственное решение, которое находится способом, аналогичным методу Лагранжа.
Многочлен H(x) называется интерполяционным многочленом Эрмита, а совокупность условий (4.10) – условиями эрмитовой интерполяции.
В общем виде построение интерполяционного многочлена Эрмита Hn(x) является непростой задачей, требующей знаний теории комплексных переменных. Полиномы Эрмита, представляющие практический интерес, будут приведены далее в главе 7.
4.2.4. Сплайн-интерполяция
Следует заметить, что использование большого числа узлов интерполяции требует применения полиномов высокого порядка, что, в свою очередь, приводит к проблемам, связанным с ошибками округления. Чтобы выполнить интерполирование, не прибегая к алгебраическим многочленам высокого порядка, используют специальный прием – кусочно-полиномиальную интерполяцию,
когда функция интерполируется полиномом степени т между любыми соседними узлами сетки.
Введем понятие сплайна.
G Сплайн1 – кусочно-полиномиальная функция, определенная на отрезке [a,b], которая при некотором разбиении a=x0<x1<…<xn=b может быть на каждом интервале (xi, xi+1) представлена в виде полинома. Иногда требуется еще и непрерывность в точках xi .
Чаще всего для кусочно-полиномиальной интерполяции
используются сплайны порядка т=1 (линейный сплайн), соответствующие аппроксимации графика функции у(х) ломаной, проходящей через точки (xi, уi), или порядка т=3 (кубический сплайн) [40].
1 Сплайн (англ) – приспособление, позволяющее плавно соединять дуги разных кривых и аналогичное по роли лекалу.
124

Аппроксимация
Рассмотрим случай, когда функция y=f(x) интерполируется кубическим полиномом (4.11) (кубическая сплайн – интерполяция)
между любыми соседними узлами сетки (рис. 4.2):
Hi (x) = ai + bi x + ci x2 + di x3 (i=1,2,…,n-1). (4.11)
Рис.4.2. Кубическая сплайн-интерполяция
Коэффициенты этого полинома на каждом интервале
определяются из условий сопряжения в узлах: |
|
|
Hi−1 (xi ) = yi |
i = 2,3,...,n , |
(4.12) |
Hi (xi ) = yi |
i =1,2,...,n −1. |
(4.13) |
Из условия непрерывности второй, а следовательно, и первой производных в точках сопряжения многочленов (при i=1,2,…,n-1) будем иметь:
Hi'−1 |
(xi ) = Hi' (xi ) , |
(4.14) |
|
Hi''−1 |
(xi ) = Hi'' (xi ) . |
(4.15) |
|
Кроме того, на границе при х=х0 и х=хn ставятся условия: |
|
||
H1'' (x0 ) = 0 , |
H n''−1 (xn ) = 0 . |
(4.16) |
|
Таким образом, получено 4(n-1) уравнений для определения всех коэффициентов (ai, bi, ci, di) кубических четырехчленов (4.11). Вместо условий (4.16) могут быть использованы и какие-либо другие краевые условия.
125

Аппроксимация
Кубическому сплайну (4.11) соответствует простая механическая аналогия – уравнение изогнутой оси стержня,
проходящего под воздействием сосредоточенных сил через заданные точки.
4.3. Среднеквадратичное приближение функций
Среднеквадратичное приближение функций – это другой подход к получению аналитических выражений функций. Особенностью таких задач является тот факт, что исходные данные
для построения тех или иных закономерностей имеют заведомо приближенный характер. Эти данные содержат погрешности измерительной аппаратуры, погрешности условий эксперимента, случайные ошибки и пр.
Предположим, что при обработке результатов какого-либо
эксперимента обнаружена некая функциональная зависимость у=f(x) между независимой переменной х и зависимой переменной у. Эта зависимость представлена в виде табл. 4.1 значений yi (i=1,2,…,n), полученных в ходе эксперимента.
Таблица 4.1
xi |
x1 |
x2 |
… |
xn |
yi |
y1 |
y2 |
… |
yn |
Если аналитическое выражение функции у=f(x) неизвестно или весьма сложно, то возникает задача найти функцию y=ϕ(х), значения которой при x=xi, возможно, мало отличалось бы от опытных данных yi, (i=1,..,n). Таким образом, исследуемая зависимость аппроксимируется функцией y=ϕ(х) на отрезке [x1,xn]:
f(x) ϕ(х). |
|
(4.17) |
|
Аппроксимирующая |
функция |
y=ϕ(х) |
называется |
эмпирической формулой или уравнением регрессии.
Эмпирические формулы не претендует на роль законов природы, а являются лишь гипотезами, более или менее адекватно описывающими опытные данные. Однако значение их весьма
126
Аппроксимация
велико. В истории науки известны случаи, когда полученная
удачная эмпирическая формула приводила к большим научным открытиям.
Для чего же нужна эта зависимость?
Если приближение (4.17) найдено, то можно:
§ просчитать значение y для любого |
x [x1 , xn ] |
(интерполяция);
§сделать прогноз о поведении исследуемого объекта вне отрезка [ x1 , x n ] (экстраполяция);
§выбрать оптимальное направление развития исследуемого процесса.
Уравнение регрессии может иметь различный вид и различный уровень сложности в зависимости от особенностей исследуемого объекта и необходимой точности представления.
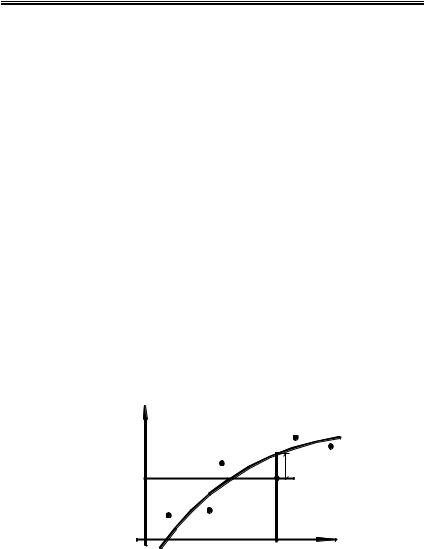
Геометрически задача построения уравнения регрессии состоит в проведении кривой L: y=ϕ(х) «возможно ближе» примыкающей к системе экспериментальных точек Mi (xi, yi), i=1,2,..,n, заданной табл. 4.1 (рис.4.3).
y |
|
|
yi |
σi |
|
M(xi,yi) |
||
|
||
|
x |
|
|
xi |
|
Рис. 4.3. Геометрический смысл задачи |
||
среднеквадратичного приближения. |
||
При нахождении уравнения регрессии интерполяционный подход заведомо является неудачным, т.к. не требуется, чтобы
127

|
Аппроксимация |
|
|
|
|
значения |
эмпирической |
функции |
ϕ(xi) |
совпадали |
с |
экспериментальными значениями yi .Достаточно, чтобы разность их [ϕ(xi)-yi] , i=1,2,..,n была мала в известном смысле.
Построение уравнения регрессии (эмпирической функции) состоит из 2 этапов:
1)выбора общего вида уравнения регрессии,
2)определения его параметров.
Удачный выбор уравнения регрессии во многом зависит от опыта экспериментатора, исследующего какой-либо процесс, явление.
Часто в качестве уравнения регрессии выбирают полином
m |
|
ϕ(x) = a0 + a1 x + a2 x2 +...+ am xm = åak xk . |
(4.18) |
k =0
Вторая задача, нахождение параметров уравнения регрессии
– более легкая и решается регулярными методами, например,
методом наименьших квадратов (МНК), который широко используется при изучении какой-либо закономерности на основе наблюдений или экспериментов.
Разработка этого метода связана с именами математиков прошлого – К.Гаусса и А.Лежандра.
4.3.1. Метод наименьших квадратов
Допустим, что результаты эксперимента представлены в виде табл. 4.1. И уравнение регрессии записывается в виде (4.18), т.е. зависит от (m+1) параметра a 0 , a1 , a 2 ,..., a m :
m |
|
ϕ(x, a0 , a1 ,a2 ,...,am ) = åak xk . |
(4.19) |
k=0
Эти параметры и определяют расположение графика эмпирической формулы относительно экспериментальных точек Mi (xi, yi), i=1,2,..,n (рис.4.3). Однако эти параметры определяются
128

Аппроксимация
не однозначно. Требуется подобрать параметры так, чтобы график
уравнения регрессии был расположен как можно ближе к системе экспериментальных точек.
Введем понятие отклонения значения уравнения регрессии (4.19) от табличного значения yi для xi :
σ i = ϕ ( x i , |
a 0 , a 1 , a 2 ,..., |
a m ) − |
y i , |
i = 1, 2 ,..., |
n .(4.20) |
|
Рассмотрим сумму квадратов отклонений |
|
|||||
|
n |
|
|
|
n |
|
S (a0 , a1 ,..., am ) = å [ϕ( xi , a0 , a1 ,..., am ) − yi ]2 = å σ i2 |
. (4.21) |
|||||
|
i=1 |
|
|
|
i=1 |
|
Согласно |
МНК |
[9,12] |
наилучшими |
коэффициентами ai |
||
(i=0,1,..,m) являются |
те, |
которые |
минимизирует |
функцию |
||
S ( a 0 , a 1 , a 2 ,..., a m ) .
Используя необходимые условия экстремума функции
нескольких переменных, получим так называемую нормальную
систему для определения неизвестных коэффициентов a0 , a1 , a 2 ,..., am :
∂ S |
|
= |
0 ; |
∂ S |
= 0 ;...; |
|
∂ S |
|
= 0 . |
(4.22) |
∂ a |
|
∂ a 1 |
∂ |
a |
|
|||||
0 |
|
|
|
m |
|
|||||
Для аппроксимирующей функции (4.19) система (4.22)
является системой линейных алгебраических уравнений относительно неизвестных a0 , a1 , a 2 ,..., am .
Если m ³ n , то существует бесконечно много многочленов (4.19), минимизмрующих функцию (4.21). Если m=n–1, то существует только один многочлен (4.19), минимизирующий функцию (4.21). Будем считать, что m<n–1.
Чем меньше m, тем проще эмпирическая формула, но это не всегда лучше.
129

Аппроксимация
4.3.2. Линейная эмпирическая формула
Самой простой и популярной является аппроксимация (приближение) прямой линией, так называемой линейной регрессией. Рассмотрим МНК для такого случая, когда эмпирическая формула (уравнение регрессии) имеет вид
y = j(x, a, b) = a + bx. |
(4.23). |
Согласно МНК наилучшими параметрами функции j(x,a,b) считаются те, для которых сумма квадратов отклонений S(a, b) является минимальной:
n |
n |
S(a, b) = å(ϕ(xi , a, b) − yi )2 |
= å(a + bxi − yi )2 (4.24) |
i=1 |
i=1 |
Для минимизации функции S=S(a,b) достаточно
продифференцировать ее по параметрам a и b и приравнять производные нулю.
В результате чего получим систему линейных алгебраических уравнений, из которой определим параметры a и b.
ì |
|
n |
n |
|
ïn × a + båxi = |
å yi , |
|
||
ï |
|
i=1 |
i=1 |
(4.25) |
í |
n |
n |
n |
|
ïïaåxi + båxi2 = åxi × yi . |
|
|||
î |
i=1 |
i=1 |
i=1 |
|
Решив эту систему относительно неизвестных а и в, получим:
|
|
n |
|
n |
n |
|
|
|
|
|
nåxi yi - åxi |
å yi |
|
|
|
||
b = |
|
i=1 |
|
i=1 |
i=1 |
, |
|
|
|
n |
|
n |
n |
|
|||
|
|
|
|
|
|
|||
|
|
nåxi2 - |
åxi |
åxi |
|
|
|
|
|
|
i=1 |
|
i=1 i=1 |
|
|
(4.26) |
|
|
|
n |
n |
n |
|
n |
||
|
|
|
|
|||||
|
|
åxi2 |
å yi - åxi yi åxi |
|
||||
a = |
i=1 |
i=1 |
i=1 |
i=1 |
. |
|
||
|
|
|
n |
n |
n |
|
|
|
|
|
nåxi2 - åxi åxi |
|
|||||
|
|
i=1 |
i=1 |
i=1 |
|
|
|
|
130
|
|
|
|
Аппроксимация |
|
|
|
||
Подставив значения а и в |
в линейную формулу |
(4.23), |
|||||||
получим математическую модель исследуемого процесса, |
|||||||||
которую можно использовать для определения значения y для |
|||||||||
любого значения x. |
|
|
|
|
|
|
|
|
|
Степень точности аппроксимации исследуемого процесса с |
|||||||||
помощью полученной функциональной зависимости может быть |
|||||||||
оценена по значению среднего квадратичного отклонения. |
|
||||||||
Под средним квадратичным отклонением функций y=f(x) |
|||||||||
и y=ϕ(x) на |
множестве |
точек |
{x1 , x2 ,.., xn } [a,b] |
понимается |
|||||
число |
|
|
|
|
|
|
|
|
|
n |
= |
1 |
ån |
[ y i |
− |
ϕ ( x i )] 2 |
, |
|
(4.27) |
|
|
n |
i = 1 |
|
|
|
|
|
|
где yi – экспериментальное значение, ϕ (xi)– значение, вычисленное |
|||||||||
по формуле (4.23) для xi. ( i=1, 2,..,n). |
|
|
|
||||||
В численных методах анализа [13] доказывается, что если |
|||||||||
среднее квадратичное отклонение |
n мало для “подавляющего |
||||||||
большинства” значений x [a, b] (т.е. в “среднем” на [a, b]), то |
|||||||||
абсолютная величина f(x)-ϕ(x) также мала на отрезке [a, |
b], т.е. |
||||||||
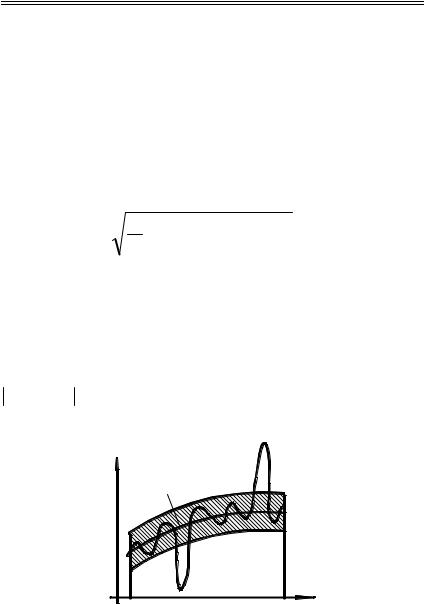
f (x) − ϕ(x) <ε для x [a, b] (рис.4.4). |
|
|
|
||||||
|
y |
|
|
|
|
y=f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=ϕ(x) |
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
0 |
a |
|
|
|
b |
|
|
|
|
Рис.4.4. Геометрический смысл степени |
|
|
||||||
|
|
|
точности аппроксимации |
|
|
|
|||
131

Аппроксимация
4.3.4. Квадратичное (параболическое) приближение
Чаще всего линейная аппроксимация является достаточно грубым приближением. При решении технических задач возникает
необходимость использования более сложной аппроксимирующей функции.
Ограничимся случаем m=2. Эмпирическая формула
(уравнение регрессии 2-го порядка) в этом случае называется
квадратичной (или параболической) и имеет вид y=ϕ(x,a,b,c)=a+bx+cx2 . (4.28)
Неизвестные параметры a, b, c согласно МНК находим из условия минимизации функции S(a,b,c), суммы квадратов
отклонений
n |
n |
S(a,b, c) = å(ϕ(xi , a,b, c) − yi )2 = å(a +bxi + cxi2 − yi )2 . |
|
i=1 |
i=1 |
|
(4.29) |
После дифференцирования и соответствующих преобразований получим нормальную систему для определения неизвестных параметров a, b, c.
|
n |
n |
n |
|
an + b å xi + cå xi2 = å yi , |
|
|||
|
i=1 |
i=1 |
i=1 |
|
n |
n |
n |
n |
|
aå xi |
+ bå xi2 |
+ cå xi3 = å yi xi , |
(4.30) |
|
i=1 |
i=1 |
i=1 |
i=1 |
|
n |
n |
n |
n |
|
aå xi2 + bå xi3 + cå xi4 = å xi2 yi . |
|
|||
i=1 |
i=1 |
i=1 |
i=1 |
|
Решая систему (4.30), получим эмпирическую формулу 2-го порядка, степень точности такого приближения для исследуемого
процесса оценивается по величине среднеквадратичного отклонения (4.27).
Если точность этого приближения не устраивает, повышают степень аппроксимирующей функции m (но надо помнить, что m<n–1).
132
