Информатика 2 сессия / Численные методы решения задач строительства на ЭВМ

Численные методы решения задач линейной алгебры

Осталось исключить неизвестное х2 из 3-го уравнения системы. Для этого реализуем описанный выше алгоритм для 2-й и 3-й строк (смотри 2-й шаг рис.2.5).

На этом первый этап метода Гаусс закончен, матрица системы приведена к треугольному виду.

На втором этапе (обратный ход метода Гаусса) последовательно найдем неизвестные, начиная с последней строки. Для этого в ячейки G12:G14 запишем формулы:

G2=D11-C11*G4-B11*G3 (для вычисления x1).

2.9.2. Решение СЛАУ с помощью надстройки «Поиск решения»

Систему линейных алгебраических уравнений можно также решить, используя надстройку «Поиск решения». При

использовании данной надстройки строится последовательность

приближений X (i) , i=0,1,…n.

Назовем вектором невязок следующий вектор:

приближение X (i) , при котором вектор невязок был бы нулевым,

т.е. добиться совпадения значений правых и левых частей системы AX=B. В качестве примера используем ту же СЛАУ.

Последовательность действий:

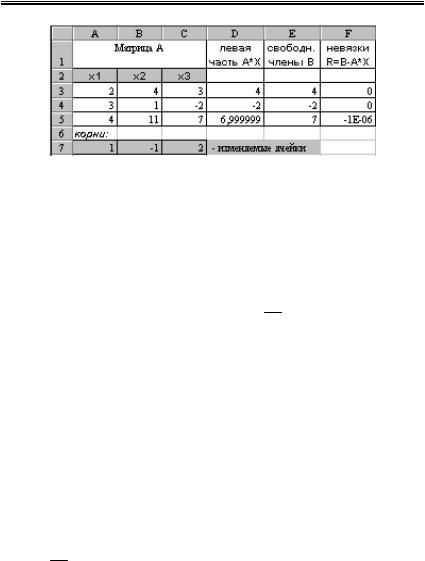
1. Заготовим таблицу, как показано на рис.2.6. Введем коэффициенты системы (матрицу А) в ячейки А3:С5.

93

Численные методы решения задач линейной алгебры

Рис.2.6. Решение СЛАУ с помощью надстройки «Поиск решения»

2. Заготовим ячейки А7:С7, где будет сформировано решение системы (х1, х2, х3). В дальнейшем будем их называть изменяемыми ячейками. Первоначально они остаются пустыми, т.е. равными нулю. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например, единицы. Эти значения можно рассматривать как

нулевое приближение решения системы, X ( 0 ) = (1,1 ,1) .

3. В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейку D3 введем и затем скопируем вниз до конца таблицы формулу:

D3=СУММПРОИЗВ (A3:C3;$A$7:$C$7).

Используемая функция СУММПРОИЗВ принадлежит категории

Математические.

4.В столбец Е запишем значения правых частей системы (матрицу В).

5.В столбец F введем невязки в соответствии с формулой (I.2), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.

6.Будет не лишним проверить правильность вычислений для

случая X ( 0 ) = (1,1 ,1) .

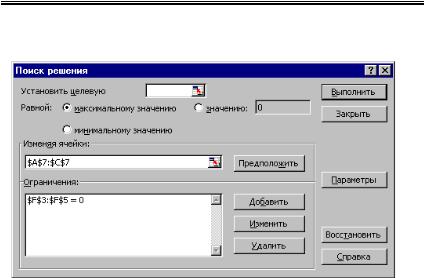
7. Зададим команду меню Сервис\Поиск решения. В окне Поиск решения (рис.2.7) в поле Изменяемые ячейки укажем блок $А$7:$С$7, а в поле Ограничения – $F$3:$F$5=0. Для этого

94

Численные методы решения задач линейной алгебры

надо щелкнуть на кнопке Добавить и ввести эти ограничения.

Щелкнем на кнопке Выполнить.

Рис. 2.7. Окно надстройки «Поиск решения»

Полученное решение систем (2.65) х1=1; х2=–1 х3=2 записано в ячейках А7:С7, рис.2.6.

2.9.3. Реализация метода Якоби средствами приложения Excel

В качестве примера рассмотрим систему уравнений (2.36), решение которой методом Якоби получено выше (пример 2.2)

8x1 + x2 - 4x3 = 6, ü 2x1 - 6x2 + x3 = -9,ïý - x1 + x2 + 4x3 = 5. ïþ

Приведем эту систему к нормальному виду:

95

Численные методы решения задач линейной алгебры

Последовательность действий

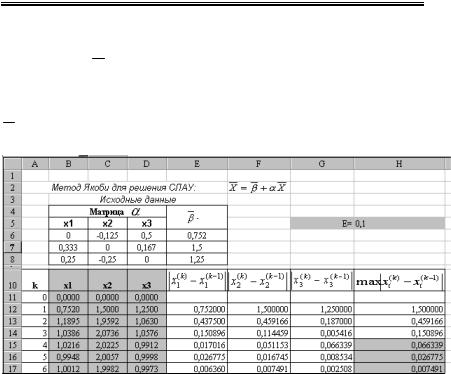
1.Заготовим таблицу, как показано на рис.2.8. Исходные данные,

матрицы α и β (2.33), введем в ячейки В6:Е8. Значение ε – в Н5.

Номер итерации k сформируем в столбце А таблицы с помощью автозаполнения. В качестве нулевого приближения выберем вектор

X (0) = {0,0,0} и введем его в ячейки В11:D11.

Рис.2.8. Схема решения СЛАУ методом Якоби

2.Используя выражения (2.67), в ячейки В12:D12 запишем формулы для вычисления первого приближения (см. раздел 2.3.1):

B12=$E$6+B11*$B$6+C11*$C$6+D11*$D$6, C12=$E$7+B11*$B$7+C11*$C$7+D11*$D$7, D12=$E$8+B11*$B$8+C11*$C$8+D11*$D$8.

Эти формулы можно записать иначе, используя функцию Excel СУММПРОИЗВ (см. раздел 2.9.2)

3.В ячейку Е12 введем формулу: E12=ABS(B11-B12) и скопируем ее вправо, в ячейки F12:G12.

4.В ячейку Н12 введем формулу для вычисления M(k), используя выражение (2.35), Н12= МАКС (E12:G12). Функция МАКС

находится в категории статистические.

96

Численные методы решения задач линейной алгебры

5.Выделим ячейки В12:Н12 и скопируем их вниз до конца таблицы. Таким образом, получим k приближений решения СЛАУ.

6.Определим количество итераций, необходимое для

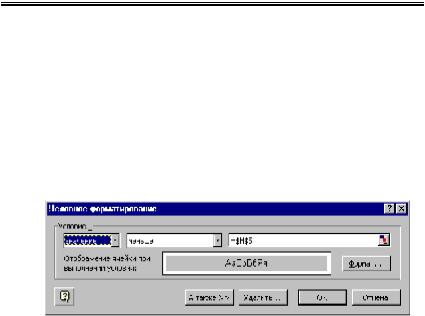
достижения заданной точности ε, и приближенное решение системы. Для этого оценим степень близости двух соседних итераций по формуле (2.35). В ячейках столбца Н установим Условный формат. Для этого выделим ячейки Н12:Н20 и

выполним команду меню Формат\Условное форматирование и в открывшимся окне сделаем установки, как показано на рис.2.9. Щелкнув по кнопке Формат, установим цвет заливки (тонирования).

Рис.2.9. Окно «Условное форматирование»

Результат такого форматирования виден на рис.2.8. Ячейки столбца Н, значения которых удовлетворяют условию (2.35), т.е. меньше ε=0,1, тонированы.

Анализируя результаты, за приближенное решение исходной

системы с заданной точностью ε=0,1 принимаем четвертую

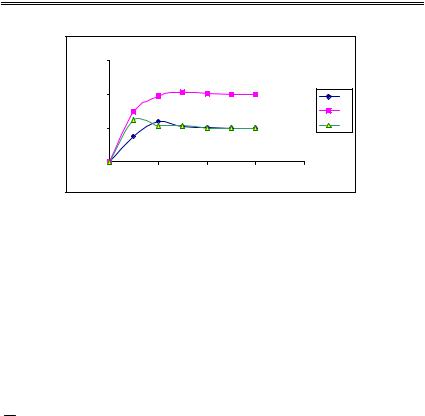
Исследуем характер итерационного процесса. Для этого выделим блок ячеек А10:D20 и, используя Мастер диаграмм, построим графики, отражающие сходимость итерационного процесса. Приведенные графики (рис.2.10) подтверждают сделанный ранее вывод о сходимости итерационного процесса.

Изменяя значение ε в ячейке Н5, получим новое приближенное решение исходной системы с новой точностью.

97

Численные методы решения задач линейной алгебры

Рис.2.10. Исследование сходимости итерационного процесса

2.9.4. Реализация метода Зейделя средствами приложения Excel

Решение той же системы линейных алгебраических уравнений получим методом Гаусса – Зейделя.

Последовательность действий:

1.Заготовим таблицу, как показано на рис.2.11.

2.В качестве нулевого приближения выберем нулевой вектор

X (0) = (0,0,0) и введем его в ячейки В11:D11.

3.В ячейках В12:D12 запишем формулы для вычисления первого приближения в соответствии с пунктом 2.3.2: B12=$E$6+B11*$B$6+C11*$C$6+D11*$D$6, C12==$E$7+B12*$B$7+C11*$C$7+D11*$D$7, D12==$E$8+B12*$B$8+C12*$C$8+D11*$D$8.

4.В столбце Н сформируем вычисление M(k) , как в предыдущем

примере

5.Установим «условный формат» в ячейках Н12-H20, это наглядно покажет количество итераций, необходимое для

достижения заданной точности ε, и приближенное решение системы.

98

Численные методы решения задач линейной алгебры

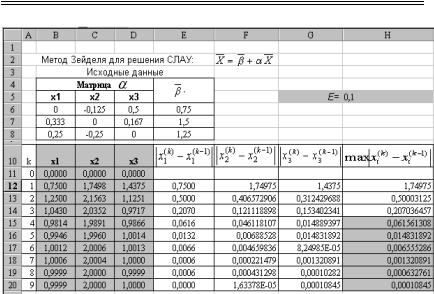
Рис.2.11. Схема решения СЛАУ методом Зейделя

Анализируя результаты, принимаем за приближенное

решение исходной системы с заданной точностью ε=0,1 вектор

99

Численные методы решения нелинейных уравнений

Глава 3. Численные методы решения нелинейных уравнений

Решение некоторых строительных задач сводится к решению достаточно сложных нелинейных уравнений, которые могут представлять собой самостоятельную задачу (например, при проектировании очистных сооружений зависимости, связывающие

проектные параметры процесса очистки являются чаще всего нелинейными) или являться составной частью более сложных задач

(например, частью расчета сооружения на устойчивость). Корни

таких уравнений сравнительно редко удается найти точными методами. Кроме того, в некоторых случаях и коэффициенты уравнения, полученные в процессе эксперимента или как результаты предварительных расчетов, известны лишь приблизительно. Следовательно, сама задача о точном определении

корней уравнения теряет смысл и важное значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности.

Нелинейные уравнения бывают алгебраическими, содержащими только алгебраические функции, например,

x2 + 5,4x −1,34 = 0, x −1 + 0,87x − 6,76 = 0

или трансцендентными, содержащими кроме алгебраических функций и другие функции, например,

где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале A < x < B.

Всякое значение x*, обращающее уравнение (3.1) в тождество, называется корнем этого уравнения, т.е. f(x*) = 0.

100

Численные методы решения нелинейных уравнений

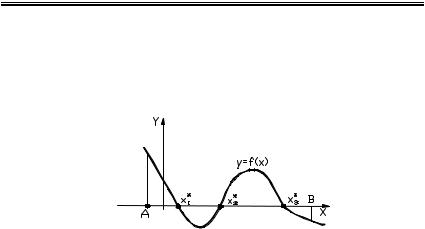
С геометрической точки зрения задача нахождения корней уравнения (3.1) эквивалентна задаче нахождения нулей функции у=f(x) или абсцисс точек пересечения графика функции c осью Х, т.е. значений xi , для которых выполняется условие f (xi) = 0 (для i=1, 2,……), рис.3.1.

Рис.3.1.Схема локализации корней

Исходя из специфики строительных задач, будем рассматривать только действительные корни уравнения (3.1).

Методы решения нелинейных уравнений делятся на прямые

(точные) и итерационные (приближенные).

Прямые методы позволяют записать корни уравнения в аналитическом виде, т.е. в виде некоторой формулы. На практике класс таких уравнений весьма невелик.

Итерационные (приближенные) методы – это методы последовательных приближений.

Алгоритм нахождения приближенных значений корней уравнения (3.1) складывается из двух этапов.

Первый этап – отделение или локализация корней. На этом этапе необходимо решить следующие задачи:

∙исследовать количество, характер и расположение

корней;

∙найти их приближенные значения (нулевые итерации).

Второй этап – уточнение приближенного корня до заданной степени точности.

101

Численные методы решения нелинейных уравнений

3.1. Отделение корней

Отделить (локализовать) корни – это значит выделить из области допустимых значений функции f(x) отрезки, в каждом из которых содержится единственный корень.

Для функции общего вида не существует универсальных методов решения задачи локализации корней. Отделить корни уравнения f(x)=0 можно разными способами:

1)Строится таблица значений функции у=f(x) на некотором отрезке x [a, b] (табулирование функции). Если окажется, что для

соседних значений аргумента значения функции имеют разные знаки, то корень функции может находиться между ними (пример

3.1).

2)Графический метод. Если удается построить график функции y=f(x), то можно определить количество и расположение нулей функции, выделяя те промежутки оси Х, где график y=f(x) пересекается с осью.

Если построение графика y=f(x) затруднительно, то исходное уравнение f(x)=0 заменяется эквивалентным ему уравнением

ϕ(x)=ψ(x) и строятся графики функций у1=ϕ(x) и у2=ψ(x).

Искомый корень является абсциссой точки пересечения этих графиков.

3) Исходя из физического смысла задачи. Убедиться в том,

что на данном отрезке x [a, b] (например, грубо определенном графическим способом) действительно имеется единственный корень уравнения (3.1), можно аналитическим способом, в основе которого лежит известная теорема математического анализа [12]:

4 Теорема 3.1. Если непрерывная на отрезке [a b] функция f(x) принимает на концах его противоположные знаки, т.е. f(a) f(b)<0 , то

внутри этого отрезка содержится по меньшей мере один корень уравнения (3.1). Корень заведомо будет единственным, если производная f'(x) существует и сохраняет постоянный знак внутри интервала (a, b), т.е. если f'(x) >0 (или f'(x<0)) при a<x<b.

102