
Информатика_2 / Раздел2.Методы численного интегрирования
.docx
|
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
Вычисления могут сопровождаться значительными погрешностями. Для снижения погрешности следует уменьшить шаг интегрирования (метод половинного шага), либо использовать более точные методы. |
|||||||||||||||||||||||||||||||||||||
|
2.2. Реализация методов в MS Excel |
|||||||||||||||||||||||||||||||||||||
|
Пример.
Вычислить площадь криволинейных
трапеций, ограниченной функцией
Последовательность действий |
|||||||||||||||||||||||||||||||||||||
|
|
D6, D7 и D8 значения нижнего и верхнего пределов интегрирования а, b и количество узлов n, соответственно. Изменяя в дальнейшем значения этих ячеек, можно вычислить значение интеграла с любой точностью e и для различных пределов интегрирования. Изменение значений этих ячеек должно привести к автоматическому пересчету всей таблицы Excel.
D9 =(D7-D6)/D8 (формулу для шага h=(b-a)/n). В12 =B6 (т.е значение а). В13 =B12+$B$9 и скопируйте ее вниз до значения нижнего предела интегрирования b. (т.е. в столбце В формируются n - значений независимой переменной х, по формуле xi+1=xi+h, i=0,1,2,….…) С12 =В12^2 (наша функция f(x) =x2) и скопируйте ее вниз.
D26 =СУММ(С12:С21)*D9 (т.е формулу для вычисления площади фигуры по методу входящих прямоугольников); D27 =СУММ(С13:С22)*D9 (т.е формулу для вычисления площади фигуры по методу выходящих прямоугольников); D28 =СУММ(E12:E21)*D9 (т.е. формулу для вычисления площади фигуры по методу средних прямоугольников); D29 =СУММ(С13:С21)*D9+(С12+С22)*D9/2 (т.е. формулу для вычисления площади фигуры по методу трапеций).
|
||||||||||||||||||||||||||||||||||||
|
В данном случае не составляет труда найти точное значение этого интеграла, используя формулу Ньютона-Лейбница:
Изменяя значения ячеек В6 (нижний предел интегрирования a), В7 (верхний предел интегрирования b), В8 (количество узлов n), С12 (формула подынтегральной функции f(x)) вы можете использовать эту таблицу для вычисления любого определенного интеграла с необходимой точностью.
Например.
Увеличьте количество узлов, т.е.
введите в ячейку В8
величину 20.
Вычислив интегральные суммы
Если
|
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||

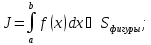
 (2.1)
(2.1) (2.2)
(2.2)

 (2.3)
(2.3) (2.4)
(2.4)

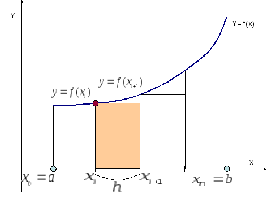








 на
отрезке [1, 3].
на
отрезке [1, 3].

 и
сравнить с полученными результатами.
и
сравнить с полученными результатами. ,
можно
оценить точность вычисления интеграла
,
можно
оценить точность вычисления интеграла

 ,
то итерационный процесс можно
закончить.
,
то итерационный процесс можно
закончить.