
Информатика_2 / Раздел1.Решение нелинейных уравнений
.docx
|
|||||||||||||||||||
|
|||||||||||||||||||
|
|||||||||||||||||||
|
Решение некоторых строительных задач сводится к решению достаточно сложных нелинейных уравнений, которые могут представлять собой самостоятельную задачу. Корни таких уравнений сравнительно редко удается найти точными методами. Кроме того, в некоторых случаях и коэффициенты уравнения, полученные в процессе эксперимента или как результаты предварительных расчетов, известны лишь приблизительно. Следовательно, сама задача о точном определении корней уравнения теряет смысл и важное значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности. Нелинейными (трансцендентными) уравнениями называют уравнения, содержащие всевозможные элементарные функции (алгебраические, логарифмические, тригонометрические или показательные). В общем виде нелинейное уравнение с одним неизвестным можно представить в виде f (x) = 0, (1.1) где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале a < x < b . |
|||||||||||||||||||
|
|
Всякое значение x*, обращающее уравнение y=f(x) в тождество, называется корнем этого уравнения, т.е. f(x*)º 0.
С геометрической точки зрения задача нахождения корней уравнения эквивалентна задаче нахождения нулей функции у=f(x) или абсцисс точек пересечения графика функции c осью Х, т.е. значений xi , для которых выполняется условие f (xi) = 0 (для i=1, 2,……).
Исходя из специфики строительных задач, будем рассматривать только действительные корни уравнения. |
||||||||||||||||||
|
Убедится в том, что на данном отрезке xÎ [a, b] (например, грубо определенном графическим способом) действительно имеется единственный корень уравнения f(x)= 0 , можно аналитическим способом, в основе которого лежит известная теорема1 математического анализа.
Методы решения нелинейных уравнений делятся на 2 группы:
Точные методы позволяют записать корни уравнения в аналитическом виде, т.е. в виде некоторой формулы. Однако, многие уравнения не имеют аналитического решения. Итерационные (приближенные) методы - это методы последовательных приближений, алгоритм которых состоит из двух этапов. 1-ый этап - отделение или локализация корней. 2-ой этап - уточнение приближенного значения корня до заданной точности e. |
|||||||||||||||||||
|
1.2. 1-ый этап решения – локализация корней |
|||||||||||||||||||
|
На этом этапе необходимо решить следующие задачи:
Принимая во внимание, что для функции общего вида не существует универсальных методов решения задачи локализации корней, рассмотрим некоторые из этих способов. 1. Строится таблица значений функции у=f(x) на некотором отрезке xÎ [А, В] (табулирование функции). Отыскивается отрезок, на концах которого функция имеет разные знаки, тогда на этом отрезке находится хотя бы один корень уравнения. 2. Графический метод. Принимая во внимание, что действительные корни уравнения f(x)=0 — это абсциссы точек пересечения графика функции y=f(x) с осью Х, достаточно построить график этой функции и отметить точки её пересечения с осью Ох. 3. Убедится в том, что на данном отрезке xÎ [a, b], определенным 1 или 2-ым способом действительно имеется единственный корень уравнения f(x)= 0 , можно аналитическим способом, в основе которого лежит известная теорема1 математического анализа. |
|||||||||||||||||||
|
1.3. Реализация 1-го этапа в MS Exсel |
|||||||||||||||||||
|
Пример.
Решить нелинейное уравнение
Задание 2.1. На 1-ом этапе необходимо
Для
этого протабулируем функцию
|
|||||||||||||||||||
|
|
Разобьем это задание на несколько более мелких заданий, выполняя их последовательно друг за другом.
Введите в ячейки:
А6 текст конец отрезка, А7 текст число отрезков, А8 текст шаг табулирования
С6: b=, D6 = 3, С7: n=, D7 = 10, С8: h=, D8 = (D6-D5)/D7
Числовые значения для Х заполняем следующим образом:
Числовые значения для f(x):
|
||||||||||||||||||
|
Поскольку
производная нашей функции
|
|||||||||||||||||||
|
1.4. 2-ой этап - уточнение корня до заданной точности |
|||||||||||||||||||
|
Этап уточнения корня заключается в построении последовательности приближенных значений корня уравнения (1.1), исходя из начального приближения - x0 : x0 , x1, x2,……xn…. (1.3) где x0 - нулевая (начальная) итерация xi - i = 1, 2,…- i-ое приближенное значения корня ( i- ая итерация)
Если эта последовательность (итерационная последовательность) имеет предел, то итерационный процесс (1.3) сходится и сходится к точному решению x* уравнения (1.1)
Таким образом, точное решение можно получить только в результате бесконечного процесса. На практике итерационный процесс должен быть ограничен конечным числом шагов (итераций) n. Количество итераций зависит от требуемой точности нахождения корня. Для прекращения итерационного процесса применяются различные критерии, зависящие от вида функции y=f(x) в окрестности корня.
|xn-1 - xn|< e (1.4)
|f(xn)|<e (1.5) Если хоты бы одно из условие (1.4) или ( 1.5) выполняется, то в качестве приближенного решения уравнения (1.1) с точностью e принимается n-я итерация, т.е. .
Если ни одно из этих условий не выполняется, то итерационный процесс (1.3) необходимо продолжить. Рассмотрим несколько итерационных методов решения нелинейных уравнений. Использование приближенных методов для решения уравнения f (x) = 0 возможно лишь в том случае, когда функция f(x) удовлетворяет следующим условиям Теоремы1:
т.е отрезок [a, b] содержит только один корень уравнения. Рассмотрим несколько итерационных методов решения нелинейных уравнений.
|
|||||||||||||||||||
|
1.5. Метод касательных. Реализация метода |
|||||||||||||||||||
|
Пусть уравнение f ( x ) = 0, на отрезке [a,b] удовлетворяет условиям теоремы 1, т.е. имеет единственный корень, и 2-ая производная f’’(x) имеет постоянный знак. Геометрически метод Ньютона заключается в замене небольшого участка дуги кривой y=f(x) касательной, проведенной в некоторой точке к этой кривой.
Рассмотрим случай, когда f ’’(x)>0 для xÎ [a, b], f(a)<0 и f(b)>0. Напомним, что знак второй производной функции легко определить из графика самой функции. Если график функции выпуклый внизу, то вторая производная функции больше нуля (f ’’ (x)>0). Если график функции выпуклый кверху , то вторая производная меньше нуля (f ’’ (x)<0). Алгоритм метода касательных |
|||||||||||||||||||
Начальное приближение x0 выбирается, исходя из условия f(x0) f ’’(x0) >0. Для функции (изображенной на рисунке) 2-ая производная больше 0 (f ’’(x0) > 0, функция выпукла книзу), f(a)<0, f(b)>0, следовательно, x0 = b (в т. x0 = а данное условие не выполняется).
|
Если хоты бы одно из условие (1.4) или ( 1.5) выполняется, то в качестве приближенного решения уравнения (1.1) с точностью e принимается n-я итерация, т.е. .
Если ни одно из условий не выполняется, то итерационный процесс необходимо продолжить. |
||||||||||||||||||
|
Аналогичным образом находиться корень и в случае, когда f ’’(x)<0 для xÎ [a b] (см. Теорема1) 2 этап. Уточнение корня уравнения. Реализация метода касательных (Ньютона) Задание 2.2. Уточнение корня уравнения
методом касательных проводим на основании теоремы 2.
Для
функции
|
|||||||||||||||||||
|
Последовательность действий. Подготовьте таблицу, как показано на рисунке
A4 текст Начало отрезка a=, D4 = 0.5, A5 текст Конец отрезка b=, D5 = 3.0, A6 текст Начальное приближение x0=, D6 = D5, A7 текст Точность вычисления e=, D7 =0,01
В13 =D6 (значение x0) C13 =B13*ln(B13)-1 (формулу для вычисления значения функции), D13 =ln(B13)+1 (формулу для вычисления значения ее производной), E13 =abs(C13) (формулу для вычисления абсолютного значения функции |f(xn)|).
Ячейки E15-E17 тонированы серым цветом с использованием Условного форматирования (см. далее) |
За приближенное значение корня уравнения с точностью e=0.01 принимается 2-я итерация, т.е. x*»1,76656.
|
||||||||||||||||||
|
Задание 2.3. Условное форматирование. Чтобы сделать наглядным окончание итерационного процесса воспользуйтесь Условным форматированием. Условное форматирование–это форматирование выделенных ячеек на основе некоторого критерия, в результате чего произойдет цветовое оформление ячеек, содержимое которых удовлетворяет заданному условию.
В результате такого форматирования ячейки столбца Е, значения которых меньше 0.01, тонированы. Таким образом, за приближенное значение корня уравнения (1.2) с точностью e=0.01 принимается 2-я итерация, т.е. x*»1,76656. Измените значение e, т.е. содержимое ячейки D7, и вы увидите, как изменится значение корня нашего уравнения. Проанализируйте результаты. |
|||||||||||||||||||
|
1.6. Метод хорд. Реализация метода |
|||||||||||||||||||
|
Пусть уравнение f( x) = 0, на отрезке [a,b] удовлетворяет условиям теоремы 1, т.е. имеет единственный корень, и производные f’(x) и f’’(x) непрерывны и имеют постоянные знаки. С геометрической точки зрения метод хорд эквивалентен замене кривой y = f(x) хордой, проходящей через точки A[a, f(a)] и B[b, f(b)].
Напомним, что знак второй производной функции легко определить из графика самой функции. Возможны несколько вариантов расположения графика функции на отрезке [a,b].
Рассмотрим 1-ый случай, когда f ’’ (x)>0 для xÎ [a,b], f(а)<0, f(b)>0 (см. рисунок ниже) Алгоритм метода хорд |
|||||||||||||||||||
Начальное приближение x0 выбирается, исходя из условия f(x0) f ’’(x0) <0. Данное условие выполняется в т. x0 = a.
|
Если хоты бы одно из условие (1.4) или ( 1.5) выполняется, то в качестве приближенного решения уравнения (1.1) с точностью e принимается n-я итерация, т.е. .
Если ни одно из условий не выполняется, то итерационный процесс необходимо продолжить. |
||||||||||||||||||
|
2 этап. Уточнение корня уравнения. Реализация метода хорд Задание 2.3. Уточнение корня уравнения (2.2) методом хорд проводим на основании теоремы 3.
Для
функции 2. Корень уравнения x* с заданной точностью ε вычисляется по формуле (1.9)
|
|||||||||||||||||||
|
Последовательность действий.
A5 текст Начало отрезка a=, E5 = 0.5, A6 текст Конец отрезка b=, E6 = 3.0, A7 текст Начальное приближение x0=, E7 = E5, A8 текст Точность вычисления e=, E8 = 0.01
В13 =Е7 (т.е. значение x0) C13 =B13*ln(B13)-1 (формулу для вычисления значения функции), D13 =$E$6-B13 (т.е. b-x), E13 =$D$10-C13, ( т.е. f(b)-f(x) ), F13 =ABS(C13), (т.е |f(x)| )
Ячейки F17-E18 тонированы серым цветом с использованием Условного форматирования (см. выше – в методе касательных) |
За приближенное решение уравнения по методу хорд с заданной точностью e=0.01 принимается 4-я итерация, т.е. x* »1,761764. |
||||||||||||||||||
|
Чтобы сделать наглядным окончание итерационного процесса воспользуйтесь Условным форматированием (установки см. в методе касательных) |
|||||||||||||||||||
|
1.7. Метод половинного деления. Реализация метода |
|||||||||||||||||||
|
Метод дихотомии заключается в последовательном уменьшении отрезка, содержащего корень уравнения, путем его деления пополам. Алгоритм метода половинного деления |
|||||||||||||||||||
|
Если условие выполняется, то полученная в результате вычислений последняя точка хn является приближённым значением корня уравнения, найденным с погрешностью e.
Если условие не выполняется, то итерационный процесс необходимо продолжить. |
||||||||||||||||||
|
2 этап. Уточнение корня уравнения. Реализация метода половинного деления (дитохомии) Задание 2.4. Уточнение корня уравнения (1.2) методом половинного деления.
|
|||||||||||||||||||
|
Последовательность действий.
A5 текст Начало отрезка a=, E5 = 0.5, A6 текст Конец отрезка b=, E6 = 3.0, A7 текст Начальное приближение x0=, E7 = (E5+E6)/2, A8 текст Точность вычисления e=, E8 = 0.01
Введите в ячейки: В13 = Е5 (значение a) C13 = Е6 (значение b) D13 = B13*ln(B13)-1 (формулу для f(а)) E13 = C13*ln(C13)-1 (формулу для f(b)) F13 = (B13+C13)/2 (формулу для вычисления середины отрезка), G13 = F13*ln(F13)-1 (формулу для f(x)) H13 = ABS(G13) (модуль значения функции)
C14 = ЕСЛИ(D13*G13<0; F13; C13), (формулу для формирования правого конца отрезка, используя функцию ЕСЛИ) .
Ячейки H19-H21 тонированы серым цветом с использованием Условного форматирования (см. выше – в методе касательных) |
За приближенное решение уравнения по методу половинного деления с заданной точностью e=0.01 принимается 6-я итерация, т.е. x* »1,7500.
|
||||||||||||||||||
|
3. Чтобы сделать наглядным окончание итерационного процесса воспользуйтесь Условным форматированием (установки см. в методе касательных)
|
|||||||||||||||||||
|
1.8. Решение нелинейного уравнения с помощью надстройки «Поиск решения» |
|||||||||||||||||||
|
Корни нелинейного уравнения можно найти, используя надстройку Excel Поиск решения. Продемонстрируем это для нашего уравнения. За нулевое приближение решения уравнения, как это видно из рисунке, можно принять х0 =2 или х0 =1,5. Последовательность действий.
А2 значение нулевого приближения корня, т.е х0 =2. B2 тоже введите значение нулевого приближения корня, т.е х =2. Значение ячейки В2 будет изменяться в процессе решения (Поиск решения). С2 введите формулу левой части уравнения, т.е. =В2*Ln(В2)-1 (смотри строку формул).
Если все было сделано правильно, то в ячейке В2 будет получено приближенное значение корня нашего уравнения, т.е. 1.76322 |
|||||||||||||||||||
|
|
|||||||||||||||||||


 (1.2),
используя различные приближенные
методы (касательных, хорд, половинного
деления (дитохомии)).
(1.2),
используя различные приближенные
методы (касательных, хорд, половинного
деления (дитохомии)). непрерывна, принимает разные знаки
на концах отрезка, т.е. f(a) f(b)<0 и
монотонна для [a, b] , т.е. производная
f’(x) сохраняет знак.
непрерывна, принимает разные знаки
на концах отрезка, т.е. f(a) f(b)<0 и
монотонна для [a, b] , т.е. производная
f’(x) сохраняет знак. для xÎ
ОДЗ и
построим ее график.
для xÎ
ОДЗ и
построим ее график.
 существует
и не изменяет знак для xÎ
[0.5, 3],
т.е. выполняются условия Теоремы1, то
анализ таблицы и графика функции
показывает, что на отрезке [0.5,
3]
уравнение имеет единственный
корень.
существует
и не изменяет знак для xÎ
[0.5, 3],
т.е. выполняются условия Теоремы1, то
анализ таблицы и графика функции
показывает, что на отрезке [0.5,
3]
уравнение имеет единственный
корень. ,
,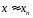
 (1.7)
(1.7)
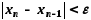 Или
Или



 (1.2)
(1.2) вторая
призводная f
’’
(x)=1/х
положительна на
всем отрезке [0.5,
3]
(функция – выпуклая книзу), f(0.5)<0,
f(3.0)>0, следовательно x0=b=3.
вторая
призводная f
’’
(x)=1/х
положительна на
всем отрезке [0.5,
3]
(функция – выпуклая книзу), f(0.5)<0,
f(3.0)>0, следовательно x0=b=3. (1.7)
(1.7)



 (1.9)
(1.9) (1.10)
(1.10)




 Или
Или 


 вторая призводная f
’’
(x)=1/х
положительна на
всем отрезке [0.5,
3]
(знак второй производной функции
можно определить и по графику функции),
f(0.5)<0,
f(3.0)>0,
следовательно x0=a=0.5
(Из
рассмотренных выше случаях у нас 1
вариант)
вторая призводная f
’’
(x)=1/х
положительна на
всем отрезке [0.5,
3]
(знак второй производной функции
можно определить и по графику функции),
f(0.5)<0,
f(3.0)>0,
следовательно x0=a=0.5
(Из
рассмотренных выше случаях у нас 1
вариант)
 ,
т.е. делим отрезок [a,
b]
пополам.
,
т.е. делим отрезок [a,
b]
пополам.
 ,
то x0
является корнем уравнения
,
то x0
является корнем уравнения
 ,
то из двух отрезков [a,
x]
и [x,
b]
выбираем тот, на концах которого
функция f(x)
имеет разные знаки (из рисунка видно,
что f(x)
> 0, f(a)<
0, f(b)
> 0,
значит
выбираем отрезок [a,
x].
Точку
b
переносим
в
x0.
,
то из двух отрезков [a,
x]
и [x,
b]
выбираем тот, на концах которого
функция f(x)
имеет разные знаки (из рисунка видно,
что f(x)
> 0, f(a)<
0, f(b)
> 0,
значит
выбираем отрезок [a,
x].
Точку
b
переносим
в
x0.


