Информатика_2 / Раздел3.Решение СЛАУ
.docx
|
||||||
|
||||||
|
3.1. Приближенные методы решения СЛАУ. Метод Якоби |
||||||
|
Метод Якоби является одним из приближенных методов решения СЛАУ. Система линейных алгебраических уравнений (СЛАУ) в общем случае имеет вид:
В некоторых случаях эту систему удобнее записывать в матричной форме:
где
А
- матрица системы,
Система (3.1-3.2) имеет единственное решение, если матрица А является невырожденной, т.е. определитель матрицы не равен 0 (detA¹0). Предполагаем, что выполняется условие «преобладания диагональных коэффициентов» матрицы системы А, т.е.
т.е. модули диагональных элементов каждой строки больше суммы модулей всех остальных элементов. Что обеспечивает сходимость итерационного процесса. Предполагаем, что диагональные элементы матрицы А отличны от нуля. Преобразуем систему (3.1) к эквивалентной ей, выражая неизвестное xi из i-ого уравнения:
Система (3.4) называется системой, приведенной к нормальному виду. Введём обозначения:
Систему (3.4) можно записать в матричной форме:
где
Систему (3.6) решаем методом последовательных приближений (итераций).
За
начальное приближение (нулевую
итерацию) принимаем столбец свободных
членов
т.е.
Используя выражение (3.6), строим последовательность приближений (итераций):
Таким образом, получили последовательность приближений:
Если
эта последовательность (4.9) имеет
предел
На практике итерационный процесс продолжается до тех пор, пока два соседних приближения не станут достаточно близкими. Критерий близости двух приближений может быть определен следующим образом:
Если условие (3.9) выполнено, то итерационный процесс прекращается и за приближенное решение системы (3.1) с заданной точностью e принимается k-ое приближение, т.е.
Условия сходимости итерационного процесса. Прежде чем применять итерационные методы для решения какой-либо системы, необходимо убедиться, что решение может быть получено, т.е. итерационный процесс сходится к точному решению. Доказывается теорема, что итерационный процесс для СЛАУ (3.1) сходится к точному решению, если матрица системы А обладает свойством «преобладания диагональных коэффициентов», т.е. выполняется условие (3.9). Если detA≠0, то с помощью линейного комбинирования уравнениями исходной системы, ее всегда можно заменить эквивалентной системой, для которой свойство «преобладания диагональных коэффициентов» выполняется.
|
||||||
|
3.2. Матричные функции в MS Excel |
||||||
|
Для решения задач линейной алгебры используются матричные функции Excel из категории математические: МУМНОЖ(<матрица1>;<матрица2>) – возвращает произведение матриц. МОБР(<матрица>) – возвращает матрицу, обратную к данной. МОПРЕД(<матрица>) – вычисляет определитель исходной квадратной матрицы. Порядок обращения к матричным функциям:
Кроме матричных функций в MS Excel имеются ряд функций для вычисления суммы произведений элементов массива, перемножая соответствующие элементы заданных массивов. С помощью данной функции в частности можно найти произведение вектора на вектор: СУММПРОИЗВ(<вектор1>,<вектор2>) – возвращает число. |
||||||
|
||||||
|
Задание 3.1. Найти решение системы линейных алгебраических уравнений.
1. Вычислите определитель системы (3.10) и сделайте вывод о существовании и единственности решения системы. Используйте матричные функции Excel. 2. Решите СЛАУ (3.10), используя надстройку Excel «Поиск решения».
В
MS
Excel
имеется возможность решения СЛАУ
Задача
Excel заключается в том, чтобы найти
такое приближение
Последовательность действий при использовании надстройки Excel «Поиск решения»: |
||||||
|
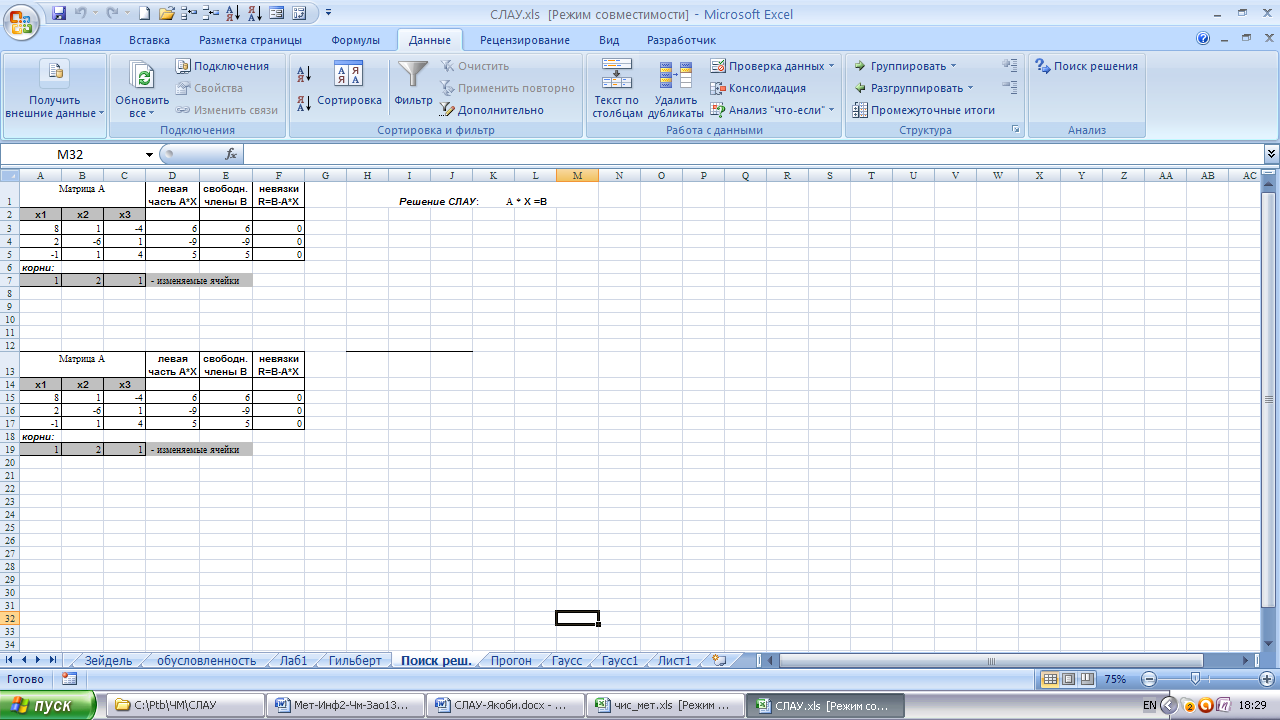
Оформите таблицу , как показано на рис.3.1. Введите
|
Рис.3.1. Решение СЛАУ с помощью надстройки
|
|||||
|
Выберите вкладку Данные\Анализ\Поиск решения (рис. 3.2.).
Решение системы (3.10.) х1=1; х2=-1 х3=2 получено в ячейках А7:С7, рис.3.1.
|
Рис. 3.2. Окно Поиск решения |
|||||
|
|
||||||
|
3.4. Реализация метода Якоби в MS Excel |
||||||
|
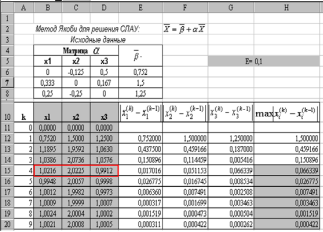
Задание 3.2. Найти решение системы линейных алгебраических уравнений (3.10) методом Якоби. Проверим, можно ли использовать изложенный выше итерационный метод для заданной системы, т.е. выполняется ли условие «преобладания диагональных коэффициентов» (3.3), что обеспечивает сходимость этого метода (|А11|=8, |А22|=6, |A33|=4) Приведем эту систему к нормальному виду:
или
в матричной форме
где
|
||||||
|
|
||||||

 , (3.1)
, (3.1)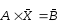 , (3.2)
, (3.2)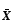 - вектор решения,
- вектор решения,
 - вектор свободных членов.
- вектор свободных членов.
 (3.3)
(3.3)
 (3.4)
(3.4)
 (3.5)
(3.5) (3.6)
(3.6) ,
,

 (3.7)
(3.7) . (3.8)
. (3.8) ,
то он является точным
решением системы
(3.1).
,
то он является точным
решением системы
(3.1).
 (3.9)
(3.9) .
. (3.10)
(3.10) с помощью надстройки «Поиск решения».
Приложение MS
Excel
использует итерационные (приближенные)
методы. Назовем вектором невязок
следующий вектор:
с помощью надстройки «Поиск решения».
Приложение MS
Excel
использует итерационные (приближенные)
методы. Назовем вектором невязок
следующий вектор: (3.11)
(3.11) ,
при котором вектор невязок был бы
нулевым, т.е. добиться совпадения
значений правых и левых частей системы
,
при котором вектор невязок был бы
нулевым, т.е. добиться совпадения
значений правых и левых частей системы
 .
. .
Для этого можно использовать функцию
СУММПРОИЗВ, из категории Математические.
.
Для этого можно использовать функцию
СУММПРОИЗВ, из категории Математические. .
. .
.

 , (3.12)
, (3.12) ,
,
 ,
,

 и
и ,
в ячейку Н5
- значение e.
,
в ячейку Н5
- значение e.