6.6.1.1.Эвольвентные червячные фрезы

Уравнение поверхности эвольвентного червяка. Эвольвентный червяк получается при движении прямойАВ (рис. 6.30), наклоненной к плоскости, перпендикулярной оси цилиндра, под углом , причем точка касания прямой АВ с цилиндром радиусом движется по винтовой линии с углом подъема . 

Рис. 6.30. К определению уравнения поверхности эвольвентного червяка

Если рассечь основной цилиндр плоскостью II-II, перпендикулярной оси, и дать последовательное положение прямой АВ при ее винтовом движении, то точка С опишет в этой плоскости некоторую плоскую кривую. Она является эвольвентной, так как ее образующая катится по винтовой линии без скольжения, а ее проекция АВ при таком перемещении катится без скольжения по окружности основного цилиндра .

Пусть и - цилиндрические координаты точки С. Начало этой системы координат совпадает с началом декартовой системы.

Связь между этими системами определяется следующими соотношениями (см. рис. 6.30):

(6.28)

За начальное положение эвольвентного червяка примем такое, когда образующая АВ будет касаться основного цилиндра в точке пересечения его с осью ОУ.

В этом начальном положении эвольвента для каждой стороны витка начинается от точки пересечения оси ОУ и начальной окружности. Координаты точки эвольвенты в начальном положении (сечение плоскостью УОZ, рис.6.31) равны:

(6.29)

Возьмем сечение II-II (см. рис.6.30) на расстоянии Х от плоскости УОZ. Эвольвента для этого сечения будет повернута на угол , а координаты точки N будут равны:

. (6.30)

Рис. 6.31. Определение угла

поворота эвольвенты

Определим . При повороте на угол точка винтовой поверхности переместится на величину шага винтовой линии ; повороту на угол будет соответствовать линейное перемещение на величину X.

 

Тогда

. (6.31)

Из уравнений (6.30) и (6.31) имеем:

.

Но - винтовой параметр, и окончательно , откуда

, (6.32)

где .

Это уравнение для левой стороны эвольвентного правозаходного червяка. Для поверхности правой стороны этого червяка будем иметь:

; (6.33)

.

Для левозаходного червяка необходимо изменить знак перед , так как направление шага противоположное.

Для торцевого сечения эвольвентного червяка , и из уравнения (6.32) получим , или

(6.34)

- левая сторона, а из уравнения (6.34) получим - правая сторона боковой поверхности. Таким образом, в плоскости, нормальной оси эвольвентного червяка, получаем эвольвенту.

Осевое сечение эвольвентного червяка найдем, положив в (6.32) и (6.33) . Тогда

(6.35)

или:

- левая сторона правозаходного червяка,

- правая сторона правозаходного червяка,

где .

Хотя уравнение (6.35) похоже на уравнение эвольвенты, кривая, определяемая уравнением , не является эвольвентой и специального названия не имеет.

Сечение эвольвентного червяка плоскостью, параллельной оси и касательной к основному червяку, определяется уравнением (рис. 6.32). Из рис. 6.32 и уравнения (6.28) имеем:

.

Рис. 6.32. Сечение эвольвентного червяка плоскостью

Но (из свойства эвольвенты), поэтому , откуда . Из рис.6.32 . Подставим найденные значения и в уравнение поверхности эвольвентного червяка (6.32) и получим:

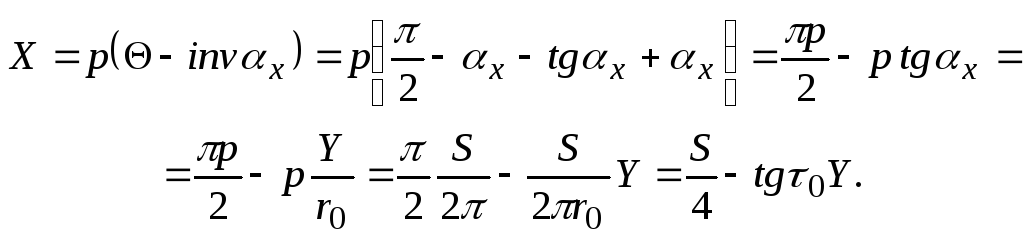(6.36)

Выражение (6.36) есть уравнение прямой с угловым коэффициентом. Благодаря этому свойству эвольвентной винтовой поверхности эвольвентный червяк нарезается резцом с прямолинейным лезвием, которое надо установить в плоскости, касательной к основному цилиндру (см. рис. 6.28,б).

Уравнение винтовой стружечной канавки. Стружечные канавки на червячных фрезах располагаются перпендикулярно направлению винтовых поверхностей основного червяка. Для правозаходного червяка стружечная канавка будет левозаходной, для левозаходного – правозаходной.

При радиальном расположении образующей стружечной канавки ее поверхность является винтовой, образованной винтовым движением прямой линии, перпендикулярной оси фрезы. Эта поверхность является частным случаем архимедовой винтовой поверхности и называется прямым геликоидом.

Рассечем винтовую канавку, соответствующую правозаходному червяку, двумя плоскостями АА и ВВ (рис. 6.33) на расстоянии друг от друга. Профиль в сечении ВВ повернут на угол против часовой стрелки относительно сечения АА. есть угол поворота прямолинейной образующей винтовой стружечной канавки, соответствующий осевому перемещению этой образующей на величину . Очевидно, должно выполнятся соотношение

Рис. 6.33. К определению уравнения стружечной канавки

или

, (6.37)

где - винтовой параметр стружечной канавки.

Уравнение режущей кромки. Уравнение режущей кромки получим, решив совместно уравнения поверхности основного червяка (6.32) и (6.33) и стружечной канавки (6.37):

(6.38)

. (6.39)

Подставив значение из уравнения (6.39) во второе уравнение системы (6.38), получим:

.

Для левой стороны правозаходного червяка:

; (6.40)

.

Для правой стороны:

;

(6.41)

.

Уравнение затылованной поверхности. Режущие кромки червячной фрезы должны одновременно принадлежать и затылованным задним поверхностям, которые должны быть винтовыми. Уравнение любой винтовой поверхности можно представить в виде

, (6.42)

где - шаг этой винтовой поверхности; и - ее цилиндрические координаты; при .

Для правой боковой затылованной поверхности имеем:

. (6.43)

Подставим значения и из уравнения (6.40) в (4.43):

;

;

. (6.44)

Значение из уравнения (6.44) подставим в уравнение (6.43), тогда получим:

	- уравнение правой боковой затылованной поверхности правозаходной фрезы,	(6.45)
	- уравнение левой боковой затылованной поверхности правозаходной фрезы.

Формулы (6.45) показывают, что боковая затылованная поверхность зуба эвольвентных червячных фрез является нелинейчатой как образованная кривой. Это является большим недостатком эвольвентных фрез, так как затрудняет их точное профилирование.

Проверка профиля этих фрез, как и всех червячных фрез, должна производиться по осевому сечению, поэтому определим осевое сечение боковой затылованной поверхности.

В уравнениях (6.45) положим , тогда:

;

(6.46)

.

В обоих уравнениях определяется по формуле . Но и при . Поэтому

. (6.47)

Задаваясь рядом значений для в пределах от окружности впадин зубьев фрезы до окружности выступов , находим соответствующие им значения и и по ним строим кривые осевого сечения. По этим кривым производится изготовление шаблонов и затыловочных резцов.

Затылование червячных эвольвентных фрез представляет значительные трудности. При радиальном затыловании (движение затыловочного резца перпендикулярно оси фрезы) резцом с криволинейной кромкой затылования поверхность не будет винтовой. Чтобы лезвие эвольвентной фрезы было расположено на винтовой затылованной поверхности, необходимо осевое затылование. Но осевое затылование из-за отсутствия специальных станков на производстве трудноосуществимо. Кроме этого, осевое затылование не обеспечивает постоянства размеров зуба фрезы при переточках.

Указанные выше обстоятельства заставляют проектировать червячные фрезы другими методами, когда прямолинейное лезвие затыловочного резца обеспечивает винтовую заднюю поверхность. С этой точки зрения более приемлемы червяки Архимеда и конволютные.