
- •Цель работы
- •Подготовка к работе
- •Вопросы для самопроверки
- •Порядок выполнения работы
- •Содержание отчёта
- •Лабораторная работа № 2
- •Цель работы
- •Вопросы для самопроверки
- •Содержание отчёта
- •Цель работы
- •Подготовка к работе
- •Вопросы для самопроверки
- •L3id1.M
- •L3id2.M
- •Содержание отчёта
- •Цель работы
- •Подготовка к работе
- •Порядок выполнения работы
- •Содержание отчета
- •Основы работы в matlab
- •1. Введение
- •2. Инструкции и переменные
- •3. Матрицы
- •4. Графика
- •5. Скрипты
- •6. Приложение
- •Режимы работы в matlab
- •Описание режимов работы
- •Пример скрипта
- •Пример работы в Simulink
- •Библиографический список
L3id1.M
Kp=30;
t=[0:0.01:1];
nc=[Kp*5];dc=[1];sysc=tf(nc,dc);
ng=[1];dg=[1 20 0];sysg=tf(ng,dg);
sys1=series(sysc,sysg);
sys=feedback(sys1,[1]);
[y,T]=step(sys,t);
plot(T,y),grid
xlabel('Время (с)')
ylabel('у(t)')
L3id2.M
Kp=30;
t=[0:0.01:1];
nc=[Kp*5];dc=[1];sysc=tf(nc,dc);
ng=[1];dg=[1 20 0];sysg=tf(ng,dg);
sys=feedback(sysg,sysc);
sys=-sys;
step(sys,t)
xlabel('Время (с)')
ylabel('у(t)')
Составьте таблицу результатов исследования и проведите анализ показателей качества системы.
Постройте модель системы в Simulinkи определите показатели качества системы при различных значениях Кp. Сделайте анализ полученных результатов и дайте сравнительную оценку способов исследования по скриптам и моделированием вSimulink.
Проведите исследование системы управления рулевым механизмом робота.
Структурная схема системы приведена на рис.3.3.

Рис.3.3. Структурная схема системы управления рулевым механизмом робота
Исходные параметры системы следующие: K=1, Кp=1, Кi=2, Т=0,1 с.
3.1. Определите в Simulinkстатическую ошибку системы при ступенчатом входном сигнале и Кp=5, Кi=0.
3.2. Определите в Simulinkстатическую ошибку системы, если управляющий входной сигнал линейный при заданных исходных параметрах системы.
3.3. Используя скрипт MATLABL3pr1.m, исследуйте влияние на показатели качества системы параметров регулятора Кpи Кi , если на входе системы сигнал треугольной формы.
L3pr1.m
% Вычисление реакции системы управления подвижным
% роботом на сигнал треугольной формы
%
numg=[10 20];deng=[1 10 0];sysg=tf(numg,deng);
[sys]=feedback(sysg,[1]);
t=[0:0.1:8.2];
v1=[0:0.1:2];v2=[2:-0.1:-2];v3=[-2:0.1:0];
u=[v1,v2,v3];
[y,T]=lsim(sys,u,t);
plot(T,y,t,u),grid
xlabel('Время (с)'),ylabel('theta (рад)')
Исследуйте качество работы одной из приведенных ниже моделей систем автоматического управления.
4.1. Система управления скоростью гоночного автомобиля (рис.3.4).
Заданная скорость
Рис.3.4. Структурная схема системы управления скоростью гоночного автомобиля
4.2. Система управления положением спутника по одной координате (рис.3.5).
+
-
Регулятор





![]()

Действительное
положение
Заданное положение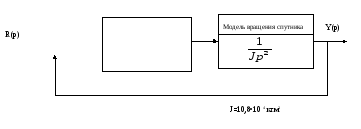
Рис.3.5. Структурная схема системы управления положением спутника
Постройте график реакции системы на ступенчатое изменение входного сигнала величиной 10 градусов.
Точное значение момента инерции спутника в общем случае неизвестно и может медленно изменяться во времени. Сравните реакции системы, когда Jуменьшится на 20% и на 50%. Параметры регулятора остаются при этом неизменными.
4.3. Система автоматического регулирования глубины погружения подводного
исследовательского робота (рис.3.6).
R(p)
Заданная глубина
Глубина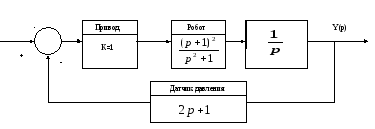
подводного исследовательского робота
4.4. Автономный самоходный аппарат для исследования Марса (рис.3.7).
F(p)
Положение аппарата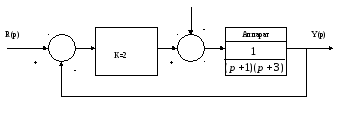
Рис.3.7. Структурная схема системы управления аппарата для исследования Марса
Требуется, чтобы возмущение (например, камни на пути движения аппарата) сказывались на работу системы незначительно, а чувствительность к изменению параметра К была малой.
Примечание: чувствительность системы к параметру К
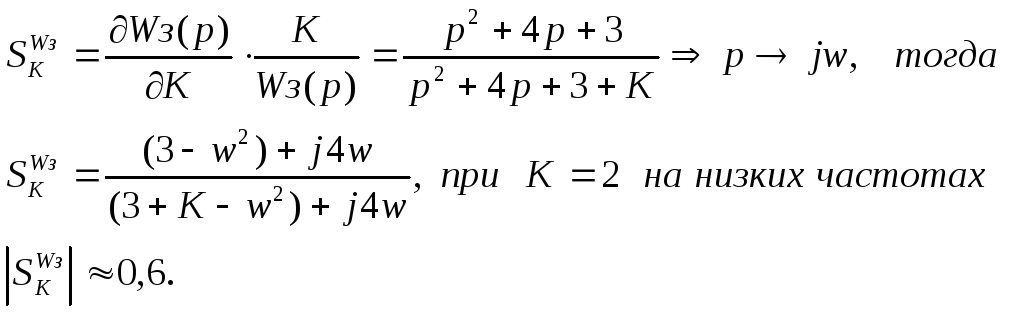 (w<0.1с-1)
(w<0.1с-1)
4.5. Система управления скоростью ракеты (рис.3.8).
Желаемая скорость
Рис.3.8. Структурная схема системы управления скоростью ракеты
4.6. Система управления углом крена самолёта с помощью элеронов (автопилот, управляющий углом крена; рис.3.9).
R(p)
Желаемый угол
крена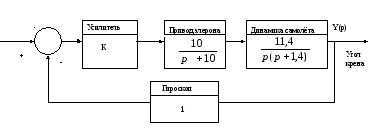
Рис.3.9. Структурная схема системы управления углом крена самолёта
