ТАУ / ТАУ Лекция 6

Идеальное дифференцирующее звено

(Вывод всех характеристик проведите самостоятельно)

Динамика процесса в таком звене описывается уравнением:

1. Переходная характеристика:

2. Импульсная переходная характеристика:

3. Передаточная функция:

4. АФЧХ:

совпадает с положительной частью мнимой оси.

5. АЧХ:

показывает: чем больше частота входного сигнала, тем больше амплитуда выходного сигнала. Эта особенность дифференцирующих звеньев вытекает непосредственно из основного уравнения: чем быстрее изменяется во времени сигнал x(t), тем больше его производная в правой части и выходной сигнал y(t).

6. ФЧХ:

Сдвиг фаз, создаваемый идеальным дифференцирующим звеном, на всех частотах одинаков и равен

7. ЛАЧХ звена:

-

прямая линия с наклоном +20 дБ/декаду, проходящая через точку с координатами

.

Р

еальное дифференцирующее звено

Динамика дифференцирующего звена представлена уравнением

1. Переходная характеристика:

График меняется скачком.

2. Импульсная переходная характеристика:

3. Передаточная функция:

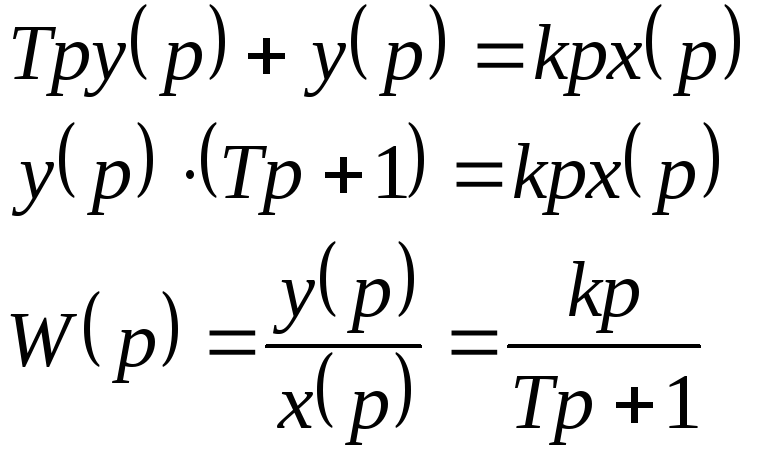
4. АФЧХ:

5. АЧХ:

6. ФЧХ:

7. ЛАЧХ:

С

труктурная схема:

Форсирующее звено

(Вывод всех характеристик проведите самостоятельно)

Динамика форсирующего звена представлена уравнением

1. Переходная характеристика:

2. Импульсная переходная характеристика:

3. Передаточная функция:

Можно представить как параллельное соединение безынерционного и идеального дифференцирующего звеньев.

4. АФЧХ:

5. АЧХ:

6. ФЧХ:

7. ЛАЧХ:

Также как и дифференцирующее звено, форсирующее звено в идеальном виде не может быть реализовано. В реальных форсирующих устройствах всегда имеются малые параметры, создающие инерционность.

Общие свойства дифференцирующих звеньев

1. При подаче на вход ступенчатого воздействия, на выходе возникает большой кратковременный импульс, а затем выход = 0.

2. Дифференцирующие звенья в статике не передают входной сигнал

3. Звенья являются фильтрами высокой частоты, вносят положительные фазовые сдвиги.

Реальное форсирующее звено (упругое)

Динамика упругого звена представлена уравнением

Передаточная функция

Существенным параметром данного звена является коэффициент.

Если , то звено подобно апериодическому,

если, то звено подобно реальному дифференциальному звену.

Форсирующее звено второго порядка

Передаточная функция

Если , то звено не относится к числу типовых, его можно представить как последовательное соединение двух форсирующих звеньев первого порядка.

Звено чистого запаздывания

Примеры - конвейеры, трубопроводы.

Звеном чистого запаздывания называется такое звено, выходная величина которого полностью повторяет входную величину, но со сдвигом во времени на величину  (время запаздывания).

Д

инамика процесса описывается уравнением:

,

где  - длительность запаздывания.

1. Переходная характеристика:

2. Импульсная переходная характеристика:

3. Передаточная функция звена:

4. АФЧХ:

представляет собой окружность с центром в начале координат и радиусом, равным единице.

5. АЧХ:

6. ФЧХ:

7

. ЛАЧХ:

С

труктурная схема:

Звенья запаздывания в большинстве случаев ухудшают устойчивость систем и делают их трудноуправляемыми.

Если ЗЗ входит в контур системы, то характеристическое уравнение системы будет уже не простым, а трансцендентным. Решение и анализ трансцендентных уравнений связаны с большими трудностямичасто в практических расчетах трансцендентную передаточную функцию раскладывают в ряд Пада и, учитывая только 2 или 3 члена ряда, приближенно заменяют дробно-рациональной функцией:

Другим возможным способом аппроксимации ЗЗ является его представление в виде последовательного соединения n инерционных звеньев первого порядка с постоянной времени

Чем больше n, тем точнее аппроксимация.