Линейная интегральная оценка

Простейшей интегральной оценкой является линейная интегральная оценка

,

которая равна площади, заключённой между прямой и кривой ПП:

Интегральная оценка учитывает как величину динамических отклонений, так и длительность их существования. Поэтому, чем меньше оценка (область S), тем лучше качество процессов управления, тем быстрее заканчивается ПП, тем меньше отклонение сигнала y(t) от y_з.

Разность под знаком интеграла равна динамической или переходной составляющей сигнала ошибки:

.

Поэтому линейную интегральную оценку чаще определяют в таком виде:

Метод Кулебакина

.

Рассмотрим следующую передаточную функцию:

.

В качестве входного сигнала x(t) рассмотрим ступенчатое воздействие r(t).

,

тогда , а.

Интегральная схема будет выглядеть так:

Если рассматривать минимум этой функции, то он будет достигаться при выполнении равенства

это идеальный переходный процесс (площадь S – min).

Т.о. выбирая коэффициенты передаточной функции в соответствии с равенством (*), можно достичь заданных показателей качества.

Модульная интегральная оценка

Но недостатком линейной интегральной оценки является то, что её можно применять только для монотонных (апериодических) переходных процессов.

Интеграл, вычисленный для знакопеременной кривой 1 , будет существенно меньше интеграла, вычисленного для апериодической кривой 2, хотя качество ПП для кривой 2 явно лучше.

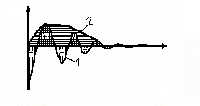
В связи с этим для колебательных переходных процессов применяют такие интегральные оценки, знакопеременность подынтегральной функции которых тем или иным способом устранена. Такими оценками являются, например, модульная интегральная оценка (ИМО – интеграл от модуля ошибки):

И её модификация (ИВМО – интеграл от взвешенного модуля ошибки)

Эта оценка придаёт больший вес тем значениям сигнала ошибки, которые имеют место в конце ПП.

Квадратичная интегральная оценка

Для колебательных процессов наиболее широко применяется квадратичная интегральная оценка (ИКО – интеграл квадрата ошибки), которая определяется по формуле:

,

которая равна площади под кривой .

Квадратичная оценка так же, как и линейная, учитывает величину и длительность отклонений. Однако, из-за возведения сигнала в квадрат, первые (большие) отклонения приобретают в конечном значении интеграла существенно больший вес, чем последующие (малые) отклонения. Поэтому минимальные значения оценки всегда соответствуют колебательным процессам с малым затуханием.

В расчетах также используют ИВКО.

Применяется и улучшенная квадратичная оценка, которая, кроме самих отклонений, учитывает с весовым коэффициентом производную отклонений.

Обычно весовой коэффициент выбирают равным желаемому времени нарастания или принимают в пределах

Апериодическая интегральная оценка

Рассмотрим ,

т.к. все величины постоянные. Здесь Т – постоянная времени, которая задается.

Е

сли выражение

,

то функция J примет минимальное значение. Это будет достигаться в том случае, если у – апериодический переходный процесс.

- оптимальный процесс с точки зрения апериодической интегральной оценки.

Следует отметить, что абсолютное значение любой интегральной оценки само по себе не представляет интереса. Они служат лишь для сопоставления различных вариантов настройки одной и той же системы.

Пример.

Передаточная функция замкнутой системы имеет вид:

Рассмотрены три оценки качества (при ступенчатом воздействии).

При t_рег=min,

Чувствительность системы

До сих пор мы предполагали, что значение параметров объекта и устройства управления остаётся в процессе эксплуатации системы постоянными. Однако, в реальных промышленных условиях из-за ряда причин (изменение температуры, износ оборудования, старение изоляции) параметры системы постепенно изменяются, и их действительные значения всегда отличаются от расчетных.

Влияние вариаций параметров системы на статические и динамические свойства называются параметрическими возмущениями, а возникающие при этом отклонения характеристик системы от расчетных значений –параметрическими погрешностями (ошибками).

Чувствительностью системы называется изменение выходных характеристик или показателей качества в зависимости от изменения параметров системы. Если система не изменяет свои выходные характеристики или показатели качества при изменении параметров системы, то такая система называется грубая (робастная).

Количественной характеристикой чувствительности системы является функция чувствительности, которая определяется как частная производная какой-либо характеристики системы (передаточная, переходная характеристика, время переходного процесса и т.д.) по варьируемому параметру, например

,- расчетное значение данного параметра.

Чаще всего на практике применяется относительная функция чувствительности:

.

Чем меньше функция чувствительность (относительная функция чувствительности), тем грубее система и, следовательно, лучше качество управления.

В разомкнутой системе изменение параметров системы приводит к отклонению выходной величины от желаемого значения. Замкнутая система, наоборот, чувствует это отклонение и пытается его скорректировать. Поэтому чувствительность системы к изменению параметров – это вопрос первостепенной важности. Основное преимущество систем с ОС – в их способности уменьшать чувствительность к изменениям параметров.

Рассмотрим случай, когда за счёт изменения параметров объекта его передаточная функция приняла выражение

Если система разомкнутая, то выходная переменная (в виде изображения Лапласа) получит приращение:

В замкнутой системе:

, отсюда

Если считать, что , то

Это выражение показывает, что в замкнутой системе изменение выходной переменной уменьшается в раз.