ТАУ / ТАУ Лекция 7

Структурные преобразования схем САУ

Для оценки точности, устойчивости и качества управления замкнутых систем необходимо знать их уравнения статики и динамики. Уравнение динамики замкнутой системы можно получить на основе совокупности уравнений отдельных элементов, образующих систему, путем последовательного исключения промежуточных переменных. Наиболее удобным для решения этой задачи объединения математических моделей элементов является метод структурных преобразований, согласно которому по структуре схемы с помощью нескольких простых правил находят ее общую (эквивалентную) передаточную функцию, а затем – соответствующее уравнение динамики.

Типовые элементы структурных схем САУ

1.	Звено
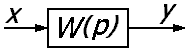
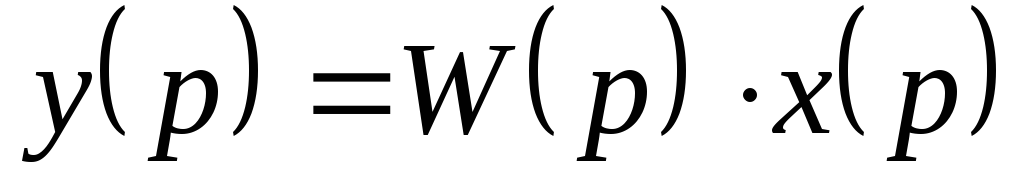
2.	Узел разветвления
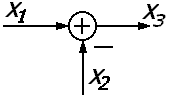
3.	Сумматор
4.	Элемент сравнения

Для упрощения (свертывания) сложных алгоритмических схем применяют три главных правила преобразования, с помощью которых определяют эквивалентные передаточные функции типовых соединений звеньев.

• Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций всех звеньев, входящих в соединение.

О

пределить передаточную функцию всей системы.

• Передаточная функция параллельно соединенных звеньев равна алгебраической сумме передаточных функций всех звеньев, входящих в соединение.

• Передаточная функция соединения с отрицательной (положительной) обратной связью равна передаточной функции прямой цепи, деленной на единицу плюс (минус) произведение передаточных функций прямой цепи и цепи обратной связи.

Соединение звеньев с отрицательной обратной связью.

Структурная схема звеньев с положительной обратной связью.

С помощью этих правил удается преобразить любую исходную алгоритмическую схему, не содержащую перекрестных связей, к одноконтурной схеме.

Алгоритмическую схему замкнутой системы управления (и саму систему) называют одноконтурной, если при ее размыкании в какой либо точке образуется цепь, не содержащая параллельных соединений и обратных связей. Цепь, полученная при размыкании замкнутой системы (см. рис. а) между точками А и В, не содержит параллельных соединений и обратных связей.

П

олучаемая при размыкании одноконтурной системы цепь последовательно соединенных элементов, стоявших внутри замкнутого контура, называется разомкнутым контуром системы (см. рис. б). В соответствии с этим определением

Передаточная функция разомкнутого контура W_р.к.(р) одноконтурной системы равна произведению передаточных функций всех элементов, стоящих внутри контура системы. Передаточные функции элементов, стоящих вне замкнутого контура, никогда не входят в произведение W_р.к.(р).

Для нашей системы

,

передаточные функции W₅(p) и W₆(p) не входят в это произведение, т.к. эти элементы стоят вне замкнутого контура.

Многоконтурные структурные схемы

При определении передаточной функции многоконтурной системы используется принцип вложенности: определяется минимальный вложенный контур и его передаточная функция. А далее переходят к следующему контуру, при этом первый контур заменяется звеном с полученной передаточной функцией.

В итоге получим схему:

Некоторые правила структурных преобразований

1	Перенос сумматоров
2	Перестановка звеньев
3	Перенос узла с выхода сумматора на вход
4	Перенос узла с входа сумматора на выход
5	Перенос узла с выхода звена на вход
6	Перенос узла со входа звена на выход
7	Перенос сумматора с выхода звена на вход
8	Перенос сумматора со входа звена на выход
9	Замена передаточных функций прямой и обратной цепи
10	Приведение к единичной обратной связи

Изображение структурных схем в виде графов

Информация о структуре системы и передаточных свойствах ее элементов может быть задана не только в виде обычной алгоритмической схемы, но и в виде сигнального графа.

Сигнальный граф системы управления представляет собой ориентированный граф – совокупность дуг, изображающих отдельные звенья и указывающих направление передачи сигнала, и вершин, соответствующих входным и выходным сигналам звеньев. Отдельному звену алгоритмической схемы, изображаемому прямоугольником, на сигнальном графе системы соответствует стрелка, соединяющая вершины х и у. Около стрелки указывается передаточная функция звена. Если к вершине подходят несколько дуг, то соответствующий ей сигнал равен сумме всех выходных сигналов этих дуг. Если из вершины исходят несколько дуг, то входные сигналы всех дуг одинаковы и равны сигналу данной вершины.

Знак, с которым сигнал вводится на алгоритмической схеме в сумматор, на сигнальном графе учитывается вместе с передаточной функцией дуги, вследствие чего сигналы всех дуг, подходящих к вершине, складываются со знаком плюс.

Д

ля сложных многоконтурных схем процедуры предварительных переносов и последовательного свёртывания для получения передаточной функции всей системы, оказываются достаточно трудоёмкими. Поэтому для таких схем целесообразно использовать формулу Мейсона

,

где - передаточные функции i-го прямого канала (i-тый прямой путь), связывающего вход с выходом ; m – число таких каналов (путей); - определитель графа, специальный полином, который определённым образом характеризует совокупность всех замкнутых цепей системы, содержащих обратные связи, и вычисляется как сумма передаточных функций разомкнутых контуров этих цепей и произведений передаточных функций разомкнутых контуров пар и троек несоприкасающихся друг с другом цепей с обратными связями:

Цепи (контура) не соприкасаются, если они не имеют общих вершин.

Полином составляется по аналогичному правилу, но только для цепей с обратными связями, не соприкасающихся с i-тым прямым каналом.

Формула Мейсона особенно удобна для применения, когда структура системы представлена в виде сигнального графа.