ТАУ / ТАУ Лекция 4

Классификация звеньев. Типовые динамические звенья

Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.

Типовые динамические звенья являются основными составными частями алгоритмических структур непрерывных систем управления, знание их характеристик существенно облегчает анализ таких систем.

Классификацию удобно осуществить, рассматривая различные частные формы дифференциального уравнения:

№ наименование а0 а1 а2 в0 в1 примечания W(p) 1 Безынерционное (пропорциональное) 0 0 1 0 к Статическое элементарное 2 Инерционное первого порядка (апериодическое) 0 Т 1 0 к Статическое инерционное 3 Инерционное второго порядка (апериодическое) Т22 Т1 1 0 к Т12Т2 Статическое инерционное 4 Инерционное второго порядка (колебательное) Т22 Т1 1 0 к Т1 <2Т2 Статическое инерционное 5 Идеальное интегрирующее 0 1 0 0 к элементарное 6 Реальное интегрирующее Т 1 0 0 к инерционное 7 Идеальное дифференцирующее 0 0 1 к 0 элементарное 8 Реальное дифференцирующее 0 Т 1 к 0 инерционное 9 Изодромное (пропорционально- интегрирующее) 0 1 0 к1 к 10 Форсирующее (пропорционально- дифференцирующее) 0 0 1 к1 к Статическое 11 Упругое (интегро- дифференцирующее, реально-форсирующее) 0 Т 1 к1 к -преобладают интегрирующие свойства -преобладают дифференцирующие свойства Статическое, инерционное

Звенья, у которых а₂ 0 и в₁ 0 обладают статизмом , т.е. однозначной связью между входной и выходной переменными в статическом режиме. Звенья – статические, или позиционные.

Звенья, у которых 2 из трех коэффициентов а₂ 0, а₁ 0, а₀ 0, обладают инерционностью (замедлением).

У звеньев 1,5,7 только 2 коэффициента 0. Они являются простейшими, или элементарными. Все остальные типовые звенья могут быть образованы из элементарных путем последовательного, параллельного и встречно- параллельного соединения.

Апериодическое звено

Динамика процесса описывается следующим уравнением:

где k  передаточный коэффициент или коэффициент усиления, Т  постоянная времени, характеризующая инерционность звена.

1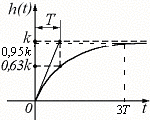. Переходная характеристика:

1)

2) В точке ноль строят касательную переходной характеристики, определяют точку пересечения с линией k. Абсцисса этой точки и есть постоянная времени.

2. Импульсная переходная характеристика, или функция веса, звена может быть получена путем дифференцирования функции h(t):

3. Передаточная функция:

П

рименим преобразование Лапласа к уравнению:

Структурная схема звена при этом будет выглядеть следующим образом:

4. АФЧХ:

Подставляя в передаточную функцию p=j, получим амплитудно-фазо-частотную функцию:

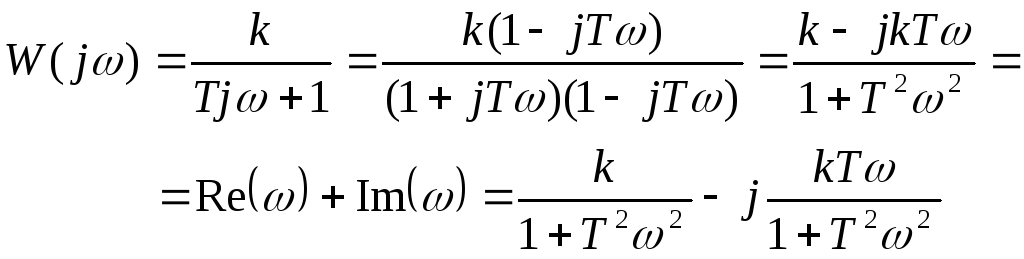
5. АЧХ:

График АЧХ строится по точкам:

Здесь _с – частота сопряжения.

Гармонические сигналы малой частоты ( <_с) пропускаются звеном хорошо – с отношением амплитуд выходной и входной величин, близким к передаточному коэффициенту k. Сигналы большой частоты ( >_с) плохо пропускаются звеном: отношение амплитуд существенно < коэффициента k. Чем больше постоянная времени Т, т.е. чем больше инерционность звена, тем меньше АЧХ вытянута вдоль оси частот, или, тем уже полоса пропускания частот.

Т.о. инерционное звено первого порядка по своим частотным свойствам является фильтром низкой частоты.

6.ФЧХ:

ФЧХ инерционного звена первого порядка равна:

Чем больше частота входного сигнала, тем больше отставание по фазе выходной величины от входной. Максимально возможное отставание равно 90⁰. При частоте _с=1/Т сдвиг фаз равен –45⁰.

7.ЛАЧХ:

Рассмотрим теперь ЛАЧХ звена. Точная ЛАЧХ описывается выражением:

При построении ЛАЧХ апериодического звена прибегают к асимптотическим методам или, другими словами, строят асимптотический график ЛАЧХ.

На втором участке наклон асимптотической ЛАЧХ составляет -20 дБ/дек.

Значение сопрягающей частоты w_c, при которой пересекаются обе асимптоты, найдем из условия

Посмотрим, что будет при построении не асимптотической, а точной ЛАЧХ:

Точная характеристика (ЛАЧХ) в точке среза будет меньше асимптотической ЛАЧХ на величину .

Существует так называемое неустойчивое апериодическое звено

Колебательное звено

Динамика процессов в колебательном звене описывается уравнением:

,

где k коэффициент усиления звена; Т постоянная времени колебательного звена;  коэффициент демпфирования звена (или коэффициент затухания).

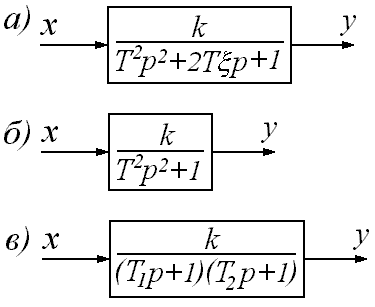
В зависимости от величины коэффициента демпфирования различают четыре типа звеньев:

а) колебательное 0<<1;

б) апериодическое звено II порядка>1;

в) консервативное звено =0;

г) неустойчивое колебательное звено <0.

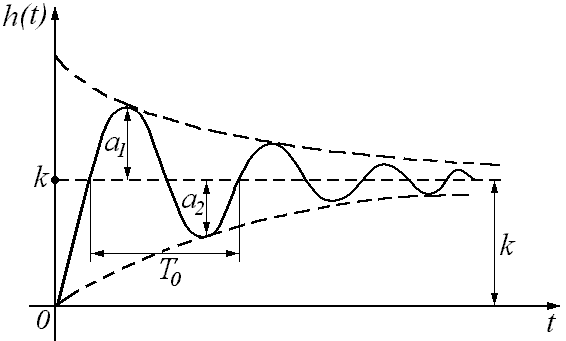
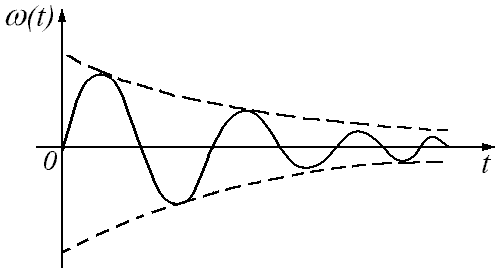
1. Переходная характеристика колебательного звена:

А

мплитуды первых двух колебаний определяют величину , или её можно найти, определив постоянную времени экспоненты, с которой происходит затухание

Чем ближе коэффициент затухания к единице, тем меньше амплитуда колебаний, чем меньше Т, тем быстрее устанавливаются переходные процессы.

При  >1 колебательное звено называется апериодическим звеном второго порядка (последовательное соединение двух апериодических звеньев с постоянными времени Т₁ и Т₂).

_c

, или можно записать так .

Здесь ₀ – величина, обратная постоянной времени (); .

Такое звено в литературе называют консервативным звеном.

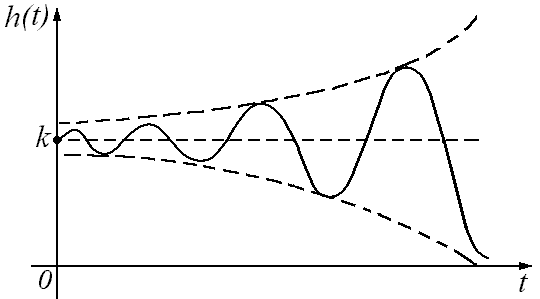
Все переходные характеристики будут колебаться вдоль величины k.

2. Импульсная переходная характеристика:

3

.Передаточная функция:

4

к

.АФЧХ:

График АФЧХ будет выглядеть следующим образом:

Это характеристика для колебательного звена и для апериодического звена второго порядка.

Для апериодического звена - .

-

- АФЧХ для консервативного звена.

5.АЧХ:

.

А

ЧХ при частоте имеет максимум (резонансный пик), равный

.

Отсюда видно, что, чем меньше коэффициент , тем больше резонансный пик.

Т

.о., по графику АЧХ видно, что колебательное звено, как и все инерционные звенья, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты; если частота гармонического входного сигнала близка к частоте собственных колебаний звена, то отношение амплитуды выходного сигнала к амплитуде входного больше передаточного коэффициента k.

6.ФЧХ:

Для случая б) график будет аналогичным, только перегиб будет чуть меньше (штриховая линия на графике).

7.ЛАЧХ:

, где

Асимптотическая ЛАЧХ колебательного звена:

Определяем наклон на втором участке:

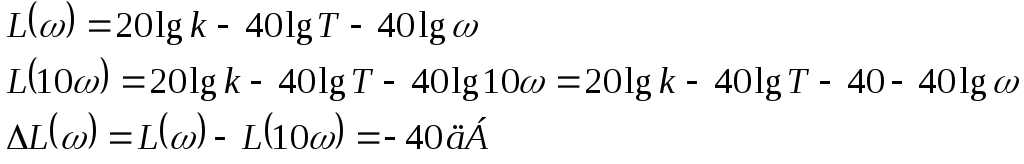
Шаблон к графику а) дается от 0 до 1 шагом в 0,1.

К

онсервативное звено:

Структурная схема колебательного звена будет выглядеть следующим образом:

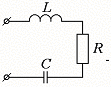
Примером колебательного звена является любая RLС- цепь.

Общие свойства статических звеньев

1. В установившемся режиме выходная переменная y однозначно связана с входной переменной x уравнением статики

2. Передаточный коэффициент звена связан с передаточной функцией соотношением

3. Звенья являются звеньями низкой частоты (кроме безынерционного), т.е. хорошо пропускают низкочастотные сигналы и плохо – высокочастотные, в режиме гармонических колебаний создают отрицательные фазовые сдвиги.