
физика / КОМПЛЕКТ_ДЛЯ_ЗО / Указания ч_2 Электромагнетизм
.pdf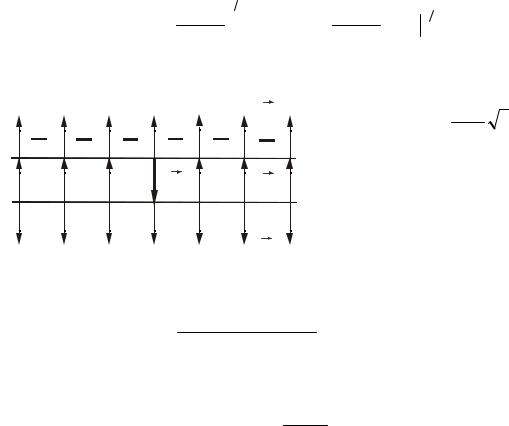
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
2τ |
|
π 3 |
r |
τ |
π 3 |
|
|
|
|
|
|
|
|
|
E = |
j 4ππ |
R |
òcosθdθ = |
j |
2ππ R sinθ |
0 |
. |
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
Подставив указанные пределы и выразив R через длину дуги (3·l = |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2πR), получим |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
E1 |
|
r |
= |
r |
|
τ |
|
3 . |
|
-q |
|
|
|
|
|
|
|
|
|
E |
j |
6ε0l |
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Из этой |
формулы видно, |
|||||||
|
|
|
|
F |
|
|
|
E1 |
|
||||||||
|
|
|
|
|
|
|
|
что вектор E совпадает с |
|||||||||
|
|
|
|
|
|
|
|
1 |
|
||||||||
q |
+ |
+ |
+ |
+ |
|
+ |
+ |
|
положительным |
|
направлением |
||||||
|
|
оси Y. |
|
|
|
|
|
|
|
||||||||
|
|
|
Рис.7 |
|
|
|
E1 |
|
Подставим значения τ и l в |
||||||||
|
|
|
|
|
|
|
|
полученную |
|
|
формулу |
и |
|||||
|
|
|
|
|
|
10−8 ×1,73 |
|
произведем вычисления: |
|
||||||||
|
|
|
Е = |
|
= 2,18 кВ / м . |
|
|
|
|
|
|
||||||
|
|
|
6 |
×8,85×10−12 ×0,15 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Найдем потенциал электрического поля в точке 0. Сначала найдем |
||||||||||||||||
потенциал dφ, создаваемый точечным зарядом dq в точке 0: |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
τdl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ = 4ππ r . |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Заменим r на R и произведем интегрирование: |
|
|
|
|
|
|
|
|||||||||
|
τ |
l |
τ l |
|
|
ϕ = |
òdl = |
|
. |
||
4ππ R |
4ππ |
R |
|||
|
0 |
0 |
0 |
|
|
Так как l = 2πR/З, то φ = τ/6ε0. Произведем вычисления:
ϕ = |
|
10 |
−8 |
= 188 В . |
|
6 |
×8,85×10−12 |
||||
|
|
||||
№ 8. На пластинах плоского конденсатора находится заряд q = 10 нКл. Площадь S каждой пластины конденсатора равна 100 см2, диэлектрик - воздух. Определить силу F, с которой притягиваются пластины.
Р е ш е н и е.
Заряд q второй пластины находится в поле напряженностью Е1, созданном зарядом первой пластины конденсатора. Следовательно, на заряд q действует сила (рис. 7)
Так как |
F = qE1. |
|
|
(1) |
||||
|
σ |
|
|
q |
|
|
||
E1 |
= |
|
= |
, |
(2) |
|||
2ε |
0 |
2ε0S |
||||||
|
|
|
|
|
||||
где σ - поверхностная плотность заряда пластины, то формула (1) с учетом выражения (2) примет вид

22
F = |
q2 |
|
2ε0 S . |
(3) |
Подставив числовые значения величин в формулу (3), подучим
F = |
|
10−18 |
|
= 5,65 ×10−4 |
H . |
|
2 |
×8,85 ×10−12 |
×10−2 |
||||
|
|
|
№ 9. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ= 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии а1 = 0,5 см и а2 = 2 см от поверхности цилиндра в средней его части.
Р е ш е н и е.
Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала:
E = −grad ϕ .
Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде
Er = − |
dϕ |
, |
или dφ = - Er dr. |
|
|
|
|
||||
|
dr |
|
|
|
|
Интегрируя это выражение, найдем разность потенциалов двух |
|||||
точек, отстоящих на расстояниях r1 и r2 от оси цилиндра: |
|
||||
|
|
|
r |
|
|
|
ϕ2 |
-ϕ1 = -ò2 |
Er dr . |
(1) |
|
|
|
|
r1 |
|
|
Так как цилиндр длинный и точки взяты вблизи его средней части, то для напряженности можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром:
|
|
Er = |
|
|
τ |
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
2πε0r |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставив выражение Е в (1), подучим |
|
|
|
|
||||||||||||||
|
|
τ |
|
|
|
r2 |
dr |
|
|
|
|
τ |
|
|
r |
|||
ϕ |
2 −ϕ1 = − |
|
|
|
|
ò |
r = − |
|
|
|
|
ln |
2 |
, |
||||
2πε |
0 |
|
|
2πε |
0 |
r |
||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
1 |
|
||||
или |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
r2 |
|
|
|
|
|
|
|
ϕ1 − ϕ2 |
= |
|
|
ln |
. |
(2) |
|||||||||||
|
2πε |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
r |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
Выразим τ и 1/2πε0 в единицах СИ: τ = 20 нКл/м = 2·10-8 Кл/м, ε0 = 8,85·10-12 Ф/м.
Так как величины r1 и r2 входят в формулу (2) в виде отношения, их можно выразить в любых, но только одинаковых единицах: r1 = R + а1 = 1,5 см; r2= R + а2 = 3 см. Подставим числовые значения в (2) и вычислим:
ϕ1 -ϕ2 = 2 ×10−8 ×1,8 ×1010 × ln 1,53 = 3,6 ×102 × 2,3 × ln2 = 250 B .

23
№ 10. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью v1
=106 м/с, чтобы скорость его возросла в n = 2 раза.
Ре ш е н и е.
Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением
заряда электрона е на разность потенциалов U: |
|
|
|
|
А = eU |
|
|
(1) |
|
Работа сил электростатического поля в данном случае равна |
||||
изменению кинетической энергии электрона: |
|
|
|
|
А = Wk 2 -Wk1 = |
mv2 |
mv2 |
, |
(2) |
2 - |
1 |
|||
|
2 |
2 |
|
|
где WК1 и WК2 - кинетические энергии электрона до и после прохождения ускоряющего поля; m - масса электрона; v1 и v2 - начальная и конечная скорости его.
Приравняв правые части равенств (1) и (2), получим
eU = |
mv2 |
− |
mv2 |
|
eU = |
mn2v2 |
- |
mv2 |
|
|
2 |
1 |
или |
|
1 |
1 |
, |
||||
2 |
2 |
|
2 |
2 |
||||||
где n = v2 / v1. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Отсюда искомая разность потенциалов |
|
|
|
|
|
|||||
|
|
|
U = mv12 |
(n2 - 1). |
|
|
|
(3) |
||
|
|
|
|
2e |
|
|
|
|
|
|
Подставим числовые значения физических величин и вычислим:
U = 9,1×10−2 × (106 )2 (22 -1)= 8,53 B . 2 ×1,6 ×10−19
№ 11. Конденсатор емкостью С1 = 3 мкФ был заряжен до разности потенциалов U1 = 40 В. После отключения от источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором емкостью С2 = 5мкФ. Какая энергия W´ израсходуется на образование искры в момент присоединения второго конденсатора?
Р е ш е н и е.
Энергия W´, израсходованная на образование искры,
W´ = W1 – W2 (1)
где W1 - энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; W2 - энергия, которую имеет батарея, составленная из первого и второго конденсаторов. Энергия заряженного конденсатора определяется по формуле
W = |
CU 2 |
|
2 , |
(2) |
где С - емкость конденсатора или батареи конденсаторов; U -разность потенциалов.
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
V |
|
|
|
|
|
|
|
Выразив в формуле (1) энергии W1 и W2 по |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
формуле (2) и принимая во внимание, что общая |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
А |
|
|
|
|
|
емкость |
|
|
|
|
параллельно |
|
|
|
|
|
соединенных |
||||||||||||||||||||
|
|
|
|
В конденсаторов равна сумме емкостей отдельных |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
конденсаторов, получим |
(С |
|
+ С |
|
)U |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
W ′ = |
|
С U |
2 |
|
− |
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|
2 |
|
2 |
, |
(3) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Рис. 8 |
|
|
|
|
|
где U2 - разность |
|
|
|
потенциалов |
на |
зажимах |
|||||||||||||||||||||||||
|
|
|
|
|
|
батареи |
|
|
|
|
параллельно |
|
|
|
|
|
соединенных |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
конденсаторов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Учитывая, что заряд после присоединения второго конденсатора |
||||||||||||||||||||||||||||||||||||||
остается прежним, выразим разность потенциалов U2 следующим образом: |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
U2 |
= |
|
|
q |
|
|
= |
|
C1U1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
C |
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
C + C |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставим выражение U2 в формулу (3): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
W ′ |
= |
С U 2 |
|
− |
(С + С )C2U |
2 |
= |
|
С U 2 |
|
− |
|
|
|
C2U 2 |
|
|
|
|
|||||||||||||||||
|
|
2 |
1 |
|
2 (C1 + C2 )2 |
1 |
2 |
|
1 |
|
|
|
2 (C1 |
+ C2 ). |
|
|
||||||||||||||||||||||
|
|
|
|
1 |
|
|
1 |
|
|
2 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
||||||
После преобразований имеем W ′ = |
1 |
|
C1C2 |
|
|
U12 . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 C1 + C2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Подставим числовые значения и вычислим W´: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
W ¢ = |
1 3×10−5 × 5 ×10−6 |
×1600 = 1,5 мДж . |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 3 |
×10−6 + 5 ×10−6 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
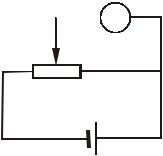
№ 12. Потенциометр с сопротивлением Rп = 100 Ом подключен к батарее, э.д.с. которой ε = 160 В и внутреннее сопротивление r = 50 Ом. Определить показание вольтметра с сопротивлением Rv = 500 Ом, соединенным с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключении вольтметра?
Р е ш е н и е.
Показание U1 вольтметра, подключенного к точкам А и В (рис. 8), определяется по формуле
U1 = I1 R1 , |
(1) |
|||||
где I1 - сила тока в неразветвленной части цепи; R1 сопротивление |
||||||
параллельно соединенных вольтметра и половины потенциометра. |
|
|||||
Силу тока I1 найдем по закону Ома для всей цепи: |
|
|||||
I1 = |
|
|
ε |
, |
(2) |
|
|
R + r |
|||||
|
|
|
|
|
||
где R - сопротивление внешней цепи. |
|
|
||||
Внешнее сопротивление R есть сумма двух сопротивлений |
|
|||||
R = |
Rп |
+ R1 , |
(3) |
|||
|
||||||
2 |
|
|
|
|
||

25
Сопротивление R1 параллельного соединения может быть найдено по
1 |
1 |
|
1 |
|
|
|
|
|
|
|
Rп RV |
|
|
|
||||
формуле |
|
= |
|
+ |
|
|
|
|
|
, откуда |
R1 = |
|
. |
|
||||
R1 |
RV |
Rп |
|
|
|
|
||||||||||||
2 |
|
Rп + 2RV |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставив числовые значения, найдем |
|
|
|
|||||||||||||||
|
|
|
|
R = |
|
|
|
100 ×500 |
|
= 45,5 Ом |
|
|
|
|||||
|
|
|
|
100 + 2 ×500 |
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
Из выражений (2) и (3) определим силу тока: |
||||||||||||||||||
|
|
|
|
I1 |
= |
|
|
|
|
|
ε |
|
= |
|
150 |
|
|
= 1,03 A . |
|
|
|
|
|
Rп |
2 |
+ R1 + r |
50 |
+ 45,5 + |
50 |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если подставить значения I1 и R1 в формулу (1), то можно определить показание вольтметра: U1 = 1,03·45,5 В = 46,9 В.
Разность потенциалов между точками А и В при отключенном вольтметре равна произведению силы тока I2 на половину сопротивления
потенциометра: |
U2 = I2 |
Rп |
= |
ε |
|
Rп |
. |
|
2 |
R + r |
2 |
||||||
|
|
|
|
|||||
|
|
|
|
п |
|
|
|
|
Подставляя в эту формулу числовые значения, получим
U2 = |
|
150 |
100 |
= 50 B . |
|
100 + 50 |
2 |
||||
|
|
||||
№13. Сила тока в проводнике сопротивлением R = 20 Ом нарастает
втечение времени t = 2 с по линейному закону от I0 = 0 до I2 = 6 А. Определить теплоту Q, выделившуюся в этом проводнике за вторую
секунду.
Р е ш е н и е. Закон Джоуля - Ленца в виде Q = I2 R t справедлив только для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого
промежутка времени и записывается в виде |
|
dQ = I2 R dt. |
(1) |
Здесь сила тока I является некоторой функцией времени. В нашем |
|
случае |
|
I = k t + I0 , |
(2) |
где k - коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т. е.
k = |
I |
= 6 = 3 A / c . |
|
t |
|
||
|
2 |
|
|
С учетом (2) формула (1) примет вид |
|
||
dQ = k2 R t2 dt. |
(3) |
||
Для определения теплоты, выделившейся за конечный промежуток времени t, выражение (3) надо проинтегрировать в пределах от t1 до t2:
t |
1 k 2 R(t |
|
− t13 ). |
Q = k 2 Rò2 t 2dt = |
23 |
||
t1 |
3 |
|
|
|
|
|
26
При определении теплоты Q, выделившейся за вторую секунду, пределы интегрирования t1 = 1 с, t2 =2 с, тогда
Q= 13 ×32 × 20 (8 -1)= 420 Дж .
№14. Электрическая цепь состоит из двух гальванических
элементов, трех сопротивлений и гальванометра (рис. 9). В этой цепи R1 = 100 Ом, R2 = 50 Ом, R3 = 20 Ом, э.д.с. элемента ε1 = 2 В. Гальванометр регистрирует ток I3 = 50 мА, идущий в направлении, указанном стрелкой. Определить э.д.с. ε2 второго элемента. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
Указание. Для расчета разветвленных цепей применяются правила Кирхгофа.
Первое правило Кирхгофа. Алгебраическая сумма сил токов,
сходящихся в узле, равна нулю, т. е. å Ii = 0.
Второе правило Кирхгофа. В любом замкнутом контуре алгебраическая сумма напряжений на отдельных участках цепи равна алгебраической сумме э.д.с., в этом контуре.
На основании этих правил можно составить уравнения, необходимые для определения искомых величин (сил токов, сопротивлений и э.д.с.). Применяя правила Кирхгофа, следует соблюдать следующую последовательность.
1.Перед составлением уравнений произвольно выбрать: а) направления токов (если они не заданы по условию задачи) и указать их стрелками на чертеже; б) направление обхода контуров.
2.При составлении уравнений по первому правилу Кирхгофа считать токи, подходящие к узлу, положительными; токи, отходящие от
|
|
|
|
|
|
|
ε |
C |
узла, отрицательными. Возможное |
||||
B |
|
|
|
|
|
|
число уравнений, составляемых по |
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||
|
+ |
|
|
|
- |
|
первому закону Кирхгофа, на |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
единицу меньше числа узлов, |
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
I1 |
|
|
I2 |
|
содержащихся в цепи. |
|
|
|||
|
|
|
|
|
|
3. |
При |
составлении |
|||||
A |
|
|
|
|
|
|
|
|
|||||
R1 |
|
|
|
F |
R2 D |
уравнений по |
второму |
правилу |
|||||
|
|
|
|
Кирхгофа надо считать, что: а) |
|||||||||
|
|
|
|
|
|
|
|
|
|||||
|
R3 |
|
Г |
|
|
|
|
падение |
напряжения |
на |
участке |
||
|
|
|
|
|
|
|
цепи (т.е. произведение IR) входит |
||||||
|
|
|
|
|
|
|
|
|
|||||
|
+ |
|
- |
|
|
|
I3 |
|
в уравнение со знаком плюс, если |
||||
|
|
|
|
|
|
||||||||
H |
|
|
G |
|
направление |
тока |
в |
данном |
|||||
|
|
ε2 |
|
участке |
совпадает с |
выбранным |
|||||||
|
|
|
|
|
|
|
|
|
направлением обхода контура; в |
||||
|
|
|
|
|
|
|
|
|
противном случае произведение IR |
||||
|
|
|
Рис. 9 |
|
входит в уравнение со знаком |
||||||||
|
|
|
|
|
|
|
|
|
минус; б) э.д.с. входит в уравнение |
||||
27
со знаком плюс, если она повышает потенциал в направлении обхода контура, т.е. если при обходе приходится идти от минуса к плюсу внутри источника тока; в противном случае э.д.с. входит в уравнение со знаком минус.
Число независимых уравнений, которые могут быть составлены по второму правилу Кирхгофа, должно быть меньше числа замкнутых контуров, имеющихся в цепи. Для составления уравнений первый контур можно выбрать произвольно. Все последующие контуры следует выбирать таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь цепи, не участвовавшая ни в одном из ранее использованных контуров. Если при решении уравнений, составленных указанным выше способом, получены отрицательные значения силы тока, то это означает, что ток через данное сопротивление в действительности течет в направлении, противоположном выбранному.
Р е ш е н и е.
Выберем направления токов, как они показаны на рис. 9, и
условимся обходить контуры по часовой стрелке. |
|
|
По первому правилу Кирхгофа для узла F имеем |
|
|
I1 – I2 – I3 = 0. |
|
(1) |
По второму правилу Кирхгофа имеем для контура АВСDFА: |
||
-I1R1 – I2R2 = -ε1, |
|
|
или после умножения обеих частей равенства на -1 |
|
|
I1 R1 + I2 R2 = ε1 . |
(2) |
|
Соответственно для контура AFGHA: |
|
|
I1 R1 + I3 R3 = ε2. |
(3) |
|
После подстановки числовых значений в формулы (1), (2) и (3) |
||
получим: |
|
|
I1 – I2 = 0,05; |
|
|
50 I1 + 25 I2 = 1; |
|
|
100 I1 + 0,05·20 = ε2. |
|
|
Перенеся в этих уравнениях неизвестные величины в левые части, а |
||
известные - в правые, получим следующую систему уравнений: |
|
|
I1 – I2 = 0,05; 50 I1 + 25 I2 = 1; |
100 I1 - ε2 = -1. |
обычными |
Эту систему с тремя неизвестными |
можно решить |
|
приемами алгебры, но так как по условию задачи требуется определить только одно неизвестное ε2 из трех, то воспользуемся методом Крамера.
Составим и вычислим определитель |
системы: |
||||||||||
= |
|
1 |
−1 |
0 |
|
= (−1) |
|
1 |
− 1 |
|
= −(25 + 50)= −75 . |
|
|
|
|
||||||||
|
|
|
|
||||||||
|
50 |
25 |
0 |
|
|
|
|||||
|
|
100 |
0 |
−1 |
|
|
|
50 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|||
Составим и вычислим определитель Δε2:
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
||
ε2 = |
|
1 |
−1 |
0,05 |
|
= 1 |
|
25 |
1 |
|
− (−1) |
|
50 1 |
|
+ 0,05 |
|
50 |
25 |
|
= |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
50 |
25 |
1 |
|
|
|
|
|
|
|
||||||||||
|
|
100 |
0 |
−1 |
|
|
|
0 |
−1 |
|
|
|
100 −1 |
|
|
|
100 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
= −25 − 50 −125 = −300. |
|
|
|
|
|
|
||||||||||
Разделив |
определитель |
Δε2 |
на |
определитель |
, найдем числовое |
|||||||||||||||
значение э.д.с. ε2:
ε2 = -300/(-75) = 4 В.
3.2.ТРЕНИРОВОЧНЫЕ ЗАДАЧИ.
1.Два шарика массой m = 1 г каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити l = 10 см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол α = 60°? ( Ответ. 79 нКл.)
2.Расстояние между зарядами q1 = 100 нКл и q2 = 60 нКл равно d = 10 см. Определить силу F, действующую на заряд q3 = 1мкКл, отстоящий на r1 = 12 см от заряда q1 и на r2 = 10 см от заряда q2. (Ответ. 51 мН)
3.Тонкий длинный стержень равномерно заряжен с линейной плотностью τ = 1,5 нКл/см. На протяжении оси стержня на расстоянии d = 12 см от его конца находится точечный заряд q = 0,2 мкКл. Определить силу взаимодействия заряженного стержня и точечного заряда. (Ответ. 2,26 мН)
4.Длинная прямая тонкая проволока имеет равномерно распределенный заряд. Вычислить линейную плотность τ заряда, если напряженность поля на расстоянии d = 0,5 м от проволоки против ее середины E = 2 В/см. (Ответ. 5,55 нКл/м)
5.С какой силой, приходящейся на единицу площади, отталкиваются две одноименно заряженные бесконечно протяженные плоскости с
одинаковой поверхностной плотностью заряда σ = 2 мкКл/м2? (Ответ. 0,23 Н/м2)
6.Какую ускоряющую разность потенциалов U должен пройти электрон, чтобы получить скорость v = 8 Мм/с? (Ответ. 182 В)
7.Заряд равномерно распределен по бесконечной плоскости с поверхностной плотностью σ = 10 нКл/м2. Определить разность потенциалов двух точек поля, одна из которых находится на плоскости, а другая удалена от нее на расстояние d = 10 см. (Ответ. 56,6 В)
8.Электрон с начальной скоростью v0 = 3 Мм/с влетел в однородное электрическое поле с напряженностью Е = 150 В/м. Вектор начальной скорости перпендикулярен линиям напряженности электрического поля. Найти: 1) силу, действующую на электрон; 2) ускорение, приобретаемое
электроном; 3) скорость электрона через t = 0,1 мкс. (Ответ. 24 аН; 26,4 Тм/с2; 4 Мм/с)
9. К батарее с э.д.с. ε = 300 В подключены два плоских конденсатора емкостью С1 = 2 пФ и С2 = 3 пФ. Определить заряд q и напряжение U на
29
пластинах конденсаторов в двух случаях: 1) при последовательном соединении; 2) при параллельном соединении. (Ответ. 1) 0,36 нКл; 189 В;
120В; 2) 0,6 нКл; 0,9 нКл; 300 В)
10.Конденсатор емкостью С1 = 600 см зарядили до разности потенциалов U = 1,6 кВ и отключили от источника напряжения. Затем к конденсатору присоединили второй, незаряженный конденсатор емкостью
С2 = 400 см. Сколько энергии W, запасенной в первом конденсаторе, было израсходовано на образование искры, проскочившей при соединении конденсаторов? (Ответ. 0,3 мДж)
11.На концах медного провода длиной l = 5 м поддерживается
напряжение U = 1 В. Определить плотность тока j в проводе. (Ответ. 1,18·107 А/м)
12.Сопротивление R1 = 5 Ом, вольтметр и источник тока соединены параллельно. Вольтметр показывает напряжение U1 = 10 В. Если заменить сопротивление R1 на R2 = 12 Ом, то вольтметр покажет напряжение U2 = 12 В. Определить э.д.с. и внутреннее сопротивление источника тока. Током через вольтметр пренебречь. (Ответ. 14 В; 2 Ом.)
13.Определить заряд, прошедший по проводу с сопротивлением R =
3 Ом при равномерном нарастании напряжения на концах провода от U1 = 2 В до U2 = 4 В в течение t = 20 с. (Ответ. 20 Кл)
14.Определить силу тока I в цепи, состоящей из двух элементов с
э.д.с. ε1 = 1,6 В и ε2 = 1,2 В с внутренними сопротивлениями r1 = 0,6 Ом и r2 = 0,4 Ом, соединенных одноименными полюсами. (Ответ. 0.4 А)
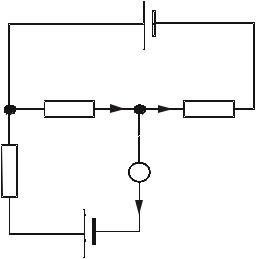
15. Три батареи с э.д.с. ε1 = 8 В, ε2 = 3 В и ε3 = 4 В с внутренними сопротивлениями r = 2 Ом каждое соединены
|
|
|
|
ε1 |
одноименными полюсами. |
Пренебрегая |
сопротивлением |
||||
|
r1 |
|
|
||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
|
|
соединительных проводов, определить токи, идущие через |
||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
батареи. (Ответ. 1,5 А; 1 А; 0,5 А) |
|
|||||
|
|
|
|
|
|
||||||
|
r2 |
|
ε2 |
16. |
Определить напряжение U на зажимах реостата |
||||||
|
|
||||||||||
|
|
||||||||||
|
|
||||||||||
|
|
сопротивлением R (рис 10), |
ε1 |
R1 |
|||||||
|
R |
|
|||||||||
|
|
если ε1 = 5 В, r1 = 1 Ом, ε2 = |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
3 В, r2 = 0,6 Ом, R = 3 Ом. |
ε2 |
|
|
R2 |
||
|
|
|
|
|
|
||||||
|
|
|
|
|
(Ответ. 3,3 В) |
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
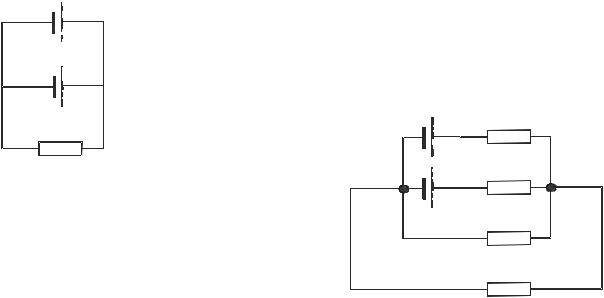
17. |
Определить |
напряжение |
на |
|
|
|
R3 |
||||
|
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|||||||||
сопротивлениях R1 = 2 Ом, R2 = R3 = 4 Ом |
|
|
|
||||||||
и R4 = |
2 |
Ом, включенных в цепь, |
как |
|
|
|
|
||||
показано на рис. 11, если ε1 |
= 10 В, ε2 |
= 4 |
R4 |
|
В. Сопротивлениями источников тока |
||||
|
||||
пренебречь. (Ответ. 6 В; 0; 4 В; 4 B)
Рис. 11
30 3.3. ПРОВЕРОЧНЫЙ ТЕСТ
Электростатика
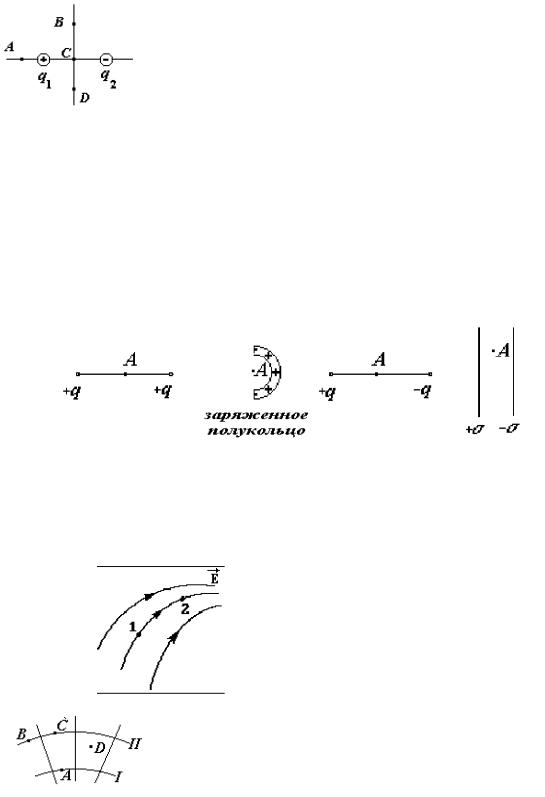
1. В какой из четырех точек А, В,С.D (см. рис). некоторый положительный заряд q3 может находиться в равновесии?
Варианты ответа:
1.В точке А. 2. В точке В. 3. В точке С. 4. В точке D.
2.Шарик массой 2,0 г, имеющий заряд 2×10-6 Кл, подвешен в воздухе на тонкой нити. Каким будет натяжение нити, если снизу шарика на
расстоянии 5 см от него расположен одноименный заряд 1,2×10-7Кл.? Варианты ответа:
1.11×10-3 Н. 2. 23×10-3 Н. 3. 0,65×10-2 Н. 4. 20×10-3 Н. 5. 8,6×10-3 Н.
3.В каких из четырех случаев распределения зарядов напряженность электростатического поля в точке А ЕА = 0 (см. рис.).
1. |
2. |
3. |
4. |
4. На рисунке приведена картина силовых линий электростатического поля. Какое соотношение для напряженностей Е и потенциалов ϕ в точках 1 и 2 верно ?
Варианты ответа:
1) Е1 < E2 , ϕ1 > ϕ2;
2) Е1 > E2 , ϕ1 < ϕ2;
3) Е1 > E2 , ϕ1 > ϕ2;
4) Е1 < E2 , ϕ1 < ϕ2;
5) Е1 = E2 , ϕ1 < ϕ2 .
5. На рис. показаны силовые линии и две эквипотенциальные поверхности I и II в электростатическом поле. Какие точки имеют одинаковые потенциалы?
Варианты ответа: В и С. 2. A и D. 3. B, C и D. 4 A, B и C. 5. A, B,C,D .
6. Плоский конденсатор между обкладками содержит диэлектрик. Конденсатор подключили к источнику напряжения, а затем удалили диэлектрик. Что при этом произошло?
