
ТАМП, ТЛП, ТСПз-3 / ЛекцииНГ / Студенты / Поверхности с плоскостью параллелизма
.ppt

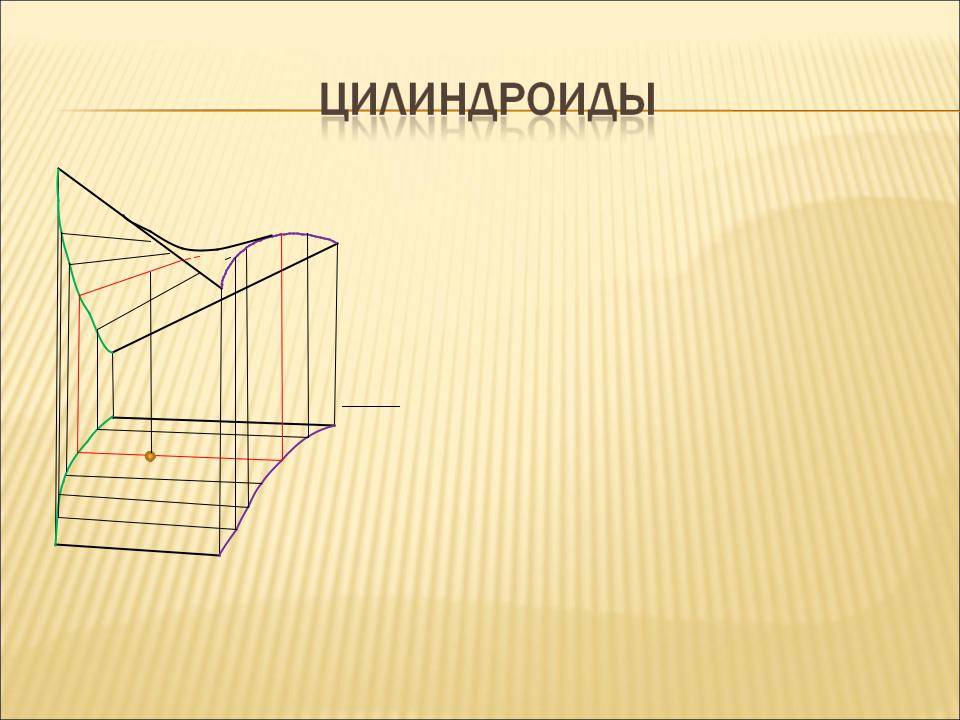
Прямолинейные образующие – скрещивающиес я прямые.
Все
образующие пересекаются с плоскостью параллелизма в несобственных точках.

Σ
m |
|
|
a |
|
|
n |
Σ |
||
m |
a |
|||
|
1 |
|||
|
1 |
|
|
|
|
|
n |
|
|
П1 |
|
1 |
|
|
|
|
|
m2
n2
a2 




 К2
К2 


Σ
1
К1 |
n1 |
|
a1 |
m1
Горизонтальные проекции движущейся образующей a параллельны горизонтальному следу Σ1 плоскости параллелизма Σ.
Фронтальные проекции образующих строят по двум точкам пересечения образующей с направляющими n и m.

Σ
m 
 n a
n a
a1 Σ1
m1 
 n1
n1
П1
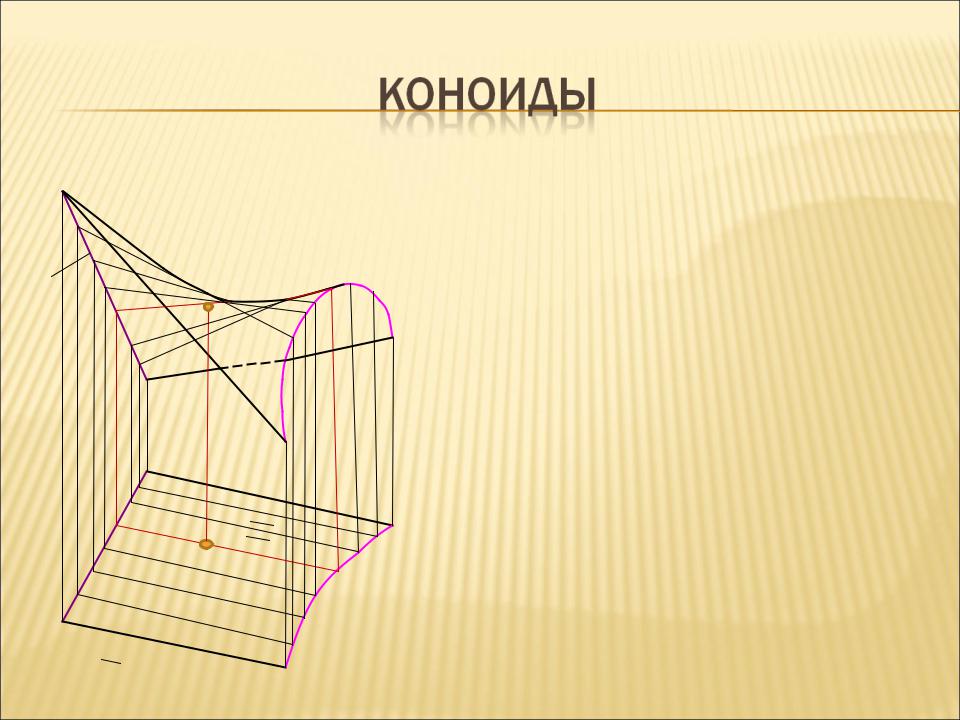
Одна из направляющих линий коноида- прямая.
m и n- направляющие, причем m-прямая, n- кривая линии; Σ - горизонтально- проецирующая плоскость, которой параллельны все образующие коноида.
m2 |
|
|
Точка К, |
|
n2 |
принадлежащая |
|
|
|
||
a2 |
(К2 |
|
поверхности коноида, |
|
) |
|
построена при |
|
|
|
помощи проходящей |
|
|
|
через нее |
a1 |
|
|
прямолинейной |
|
К1 |
n1 |
образующей a. |
m1
Σ1
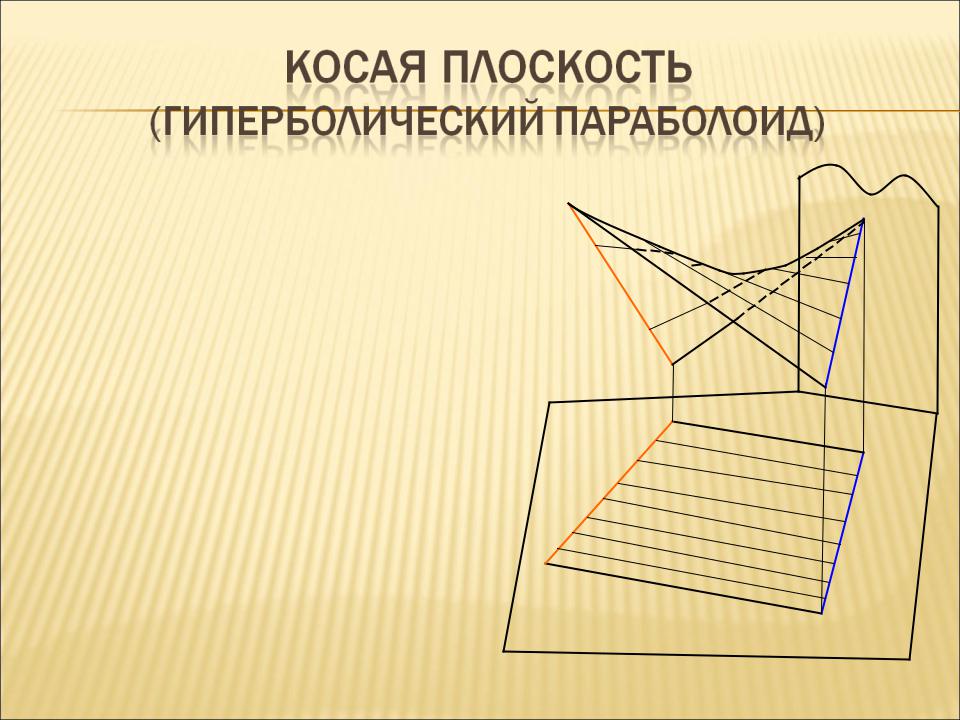
Косая плоскость образуется непрерывным перемещением прямолинейной образующей a по двум направляющим – скрещивающимся прямым m и n-
параллельно |
|
некоторой плоскости |
|
параллелизма Σ |
П1 |
Σ
m




an
Σ1
m |
n1 |
1 |
a1

Для построения точки К этой поверхности по заданной горизонтальной проекции К1 использована образующая прямая a.
Для построения той же точки М по заданной фронтальной ее проекции M2 может быть использована произвольная линия на поверхности косой плоскости , например b.
m2
m
1
|
M2 |
a2 К2 |
n1 |
|
|
|
b2 |
a1  К1
К1
 M
M
1
Σ1 |
n1 |
|
b1 |
