Кривые линии
Определение
Кривую линию можно рассматривать как непрерывное множество последовательных положений точки, движущейся в пространстве, т.е. как траекторию движущейся точки.
Если координаты любой точки кривой удовлетворяют некоторому уравнению, то такие кривые называются закономерными.
Способы образования кривой. Виды кривой
Способы образования кривой:
Движение в пространстве
Пересечение поверхности плоскостью
Пересечение поверхностей Виды кривой:
Плоские (все точки принадлежат плоскости)
Пространственные (точки кривой не принадлежат одной плоскости)
Локальные элементы кривой
Секущей называется прямая, пересекающая кривую в одной, двух или более точках.
Касательная к кривой в точке
М определяется как предельное положение секущей, проходящей через М и соседнюю точку N кривой, при условии, что N стремится к М.
Нормаль (для плоских кривых)
– это прямая, перпендикулярная касательной в точке касания М.
→
m
→
M s N 
→
n
Кривые эллиптического типа
Эллипс представляет собой геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная.
Частным видом эллипса является
окружность.
В начертательной геометрии эллипсы чаще всего рассматривают как проекции окружности.
Эллипс
Каноническое уравнение эллипса имеет вид:
,где b2=a2 – c2.
Оси координат являются осями симметрии.
Точка О (точка пересечения осей) называется центром эллипса.Отрезки, соединяющие противоположные вершины эллипса, равные 2a и 2b, называются соответственно большой и малой осями эллипса.
Два фокуса эллипса расположены на расстоянии 2с (фокусном расстоянии).
y
|
|
|
E |
|
b |
|
|
nE |
tE |
|
O |
|
x |
|
F1 |
|
|
||
c |
c |
|
F2 |
|
b |
|
|
|
|
|
a |
|
a |
|
Эллипс
Диаметры эллипса – это отрезки прямых, проходят через центр эллипса.
Геометрическим местом середин хорд, параллельных одному из диаметров эллипса, является диаметр, сопряженный данному. Диаметры 2a1 и 2b1 являются сопряженными.
Большая и малая оси эллипса являются сопряженными взаимно перпендикулярными диаметрами.
tE
E1
O1
2 |
|
|
b |
a1 |
|
1 |
||
2 |
Касательные, проведенные к эллипсу в концах какого- либо диаметра, параллельны другому диаметру, сопряженному с первым.
Проекции окружности
Без искажения в |
|
натуральную величину |
|
(если ее плоскость |
|
параллельна |
|
плоскости проекции) |
П2 |
|
x |
В виде отрезка (если |
П1 |
|
|
она перпендикулярна |
|
плоскости проекции) |
|
Эллипс (в общем |
|
случае) |
|
О2
О1
Построение проекции окружности
Дано:
Окружность данного диаметра принадлежит горизонтально- проецирующей плоскости Σ(Σ1).
Горизонтальная проекция окружности А1В1 равна диаметру и
совпадает со следом плоскости Σ.Большая ось эллипса является горизонтально-проецирующей прямой и на П2 изображается в
натуральную величинуНеобходимо построить проекцию окружности на П2.
22 |
12 |
32 |
П2 |
A2 |
O2 |
x |
|
|
П1 |
|
|
31
O1≡O4 ≡11
21
1 |
A1≡A4 |
П |
24 |
x П |
|
4 |
|
B2
Σ1
B1≡B4
34
14
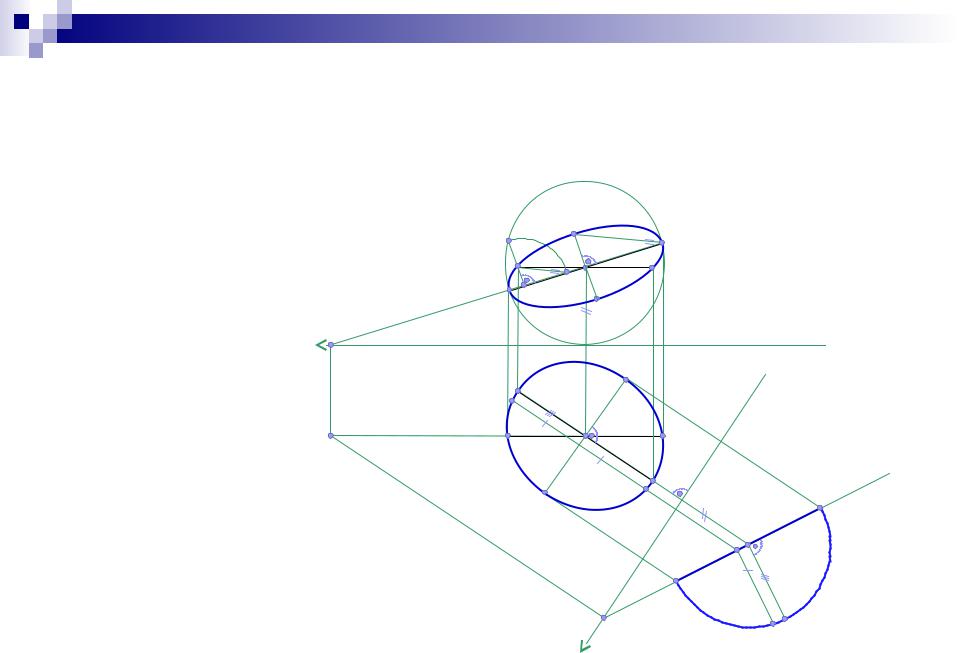
Задача: Построение проекций окружности
Дано: |
|
Окружность лежит в |
|
плоскости общего |
|
положения Σ (h∩f) |
x B2 |
Диаметр окружности |
|
12 совпадает с |
|
горизонталью, диаметр |
|
34 – с фронталью. |
B1 |
|
|
Построить проекции |
|
окружности |
|
|
K2 |
|
82 |
42 |
|
|
|
||
|
|
22 |
h2 |
|
|
12 |
|
||
|
|
K2’ О2 |
|
|
f2 |
32 |
E2 |
|
|
92 |
|
|||
|
|
|
11 |
61 |
|
71 |
31 |
41f1 |
О1 |
|
|
21 h1 |
|
|
П x1 |
|
|
|
|
4 |
|
|
|
|
|
П |
|
51 |
71’ |
|
|
≡О5 |
5 |
|
|
64 ≡65 |
|||
|
|
|
24 |
||
|
|
|
≡ |
|
|
|
|
14 |
|
|
|
|
|
≡ |
|
|
|
|
|
О4 |
|
|
|
|
|
|
|
54 ≡55 |
П |
1 |
|
B4 |
15 |
|
П |
|
75 |
|
x |
1 |
4 |
|
|
|
|
|