
Поверхности вращения
Поверхность закрытая: меридиональное сечение – замкнутая кривая, пересекающая ось в 2-х точках
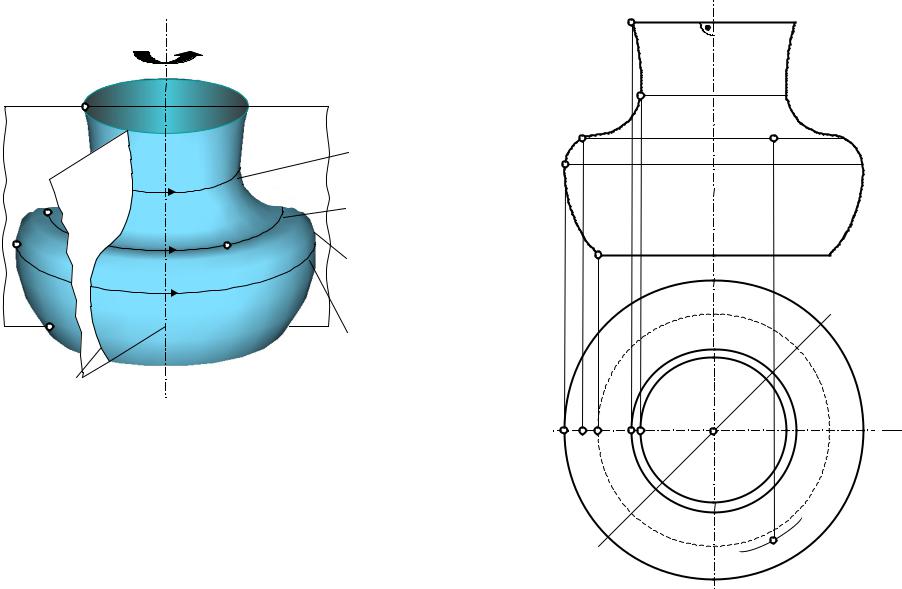
П В общего вида – вращением образующей (плоской или пространственной кривой) вокруг оси вращения (обычно – горизонтально-проецирующей)

|
|
|
П В общего вида |
|
i2 |
||
Ф(а, i) |
|
|
|
A2 |
|
||
Ось (i) |
|
|
|
||||
|
|
|
|
||||
A |
|
|
|
|
B2 |
|
|
|
|
F |
C2 |
|
|
K2 |
|
|
|
|
|
|
|||
|
A’ |
|
Горло |
D2 |
|
|
|
|
|
|
|
|
|
||
Θ |
|
|
Параллель |
|
|
|
|
|
|
|
|
|
|
|
|
D |
C’ |
K |
Главный |
E2 |
|
|
|
|
|
|
|
||||
|
|
|
меридиан (а) |
|
|
|
|
E |
|
|
Экватор (е) |
|
|
|
|
|
|
|
|
|
|
|
|
Меридиан |
|
|
|
C1 |
E1 B |
|
F1 |
Произвольная точка образующей при вращении |
1 |
||||||
вокруг оси описывает окружность – параллель. |
|
|
|
||||
D1 |
A1 |
|
i1 |
||||
Наиб. – экватор, |
|
|
|
||||
|
|
|
|
|
|
||
наим. – горловина |
|
|
Θ1 |
|
|
|
|
– очерковые линии |
Радиус параллели – |
|
|
|
|||
|
|
|
|
||||
поверхности |
расстояние от точки до оси. |
|
|
|
K1 |
||
|
|
|
П В общего вида |
|
i2 |
|||
Ф(а, i) |
|
|
|
A2 |
|
|||
|
Ось (i) |
|
|
|
||||
|
|
|
|
|
||||
A |
|
|
|
|
B2 |
|
|
|
|
|
F |
C2 |
|
|
K2 |
||
|
|
|
|
|
||||
|
A’ |
|
Горло |
D2 |
|
|
|
|
|
|
|
|
|
|
|||
Θ |
|
|
Параллель |
|
|
|
|
|
|
|
|
|
|
|
|
||
D |
C’ |
K |
Главный |
E2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
меридиан (а) |
|
|
|
|
|
E |
|
|
Экватор (е) |
|
|
|
|
|
|
|
|
|
|
|
|
||
Меридиан |
|
|
|
C1 |
E1 B |
|
F1 |
|
Меридиональные плоскости – через ось |
1 |
|||||||
|
|
|
||||||
D1 |
A1 |
|
|
|||||
вращения. (Главная – параллельная плоскости |
|
|
||||||
|
|
|
|
|||||
проекции) |
|
|
|
|
|
|
|
|
Меридианы – линии пересечения м. |
Θ1 |
|
|
|
||||
плоскостями поверхности. (Главный – главной м. |
|
|
|
|||||
|
|
|
K1 |
|||||
п. (очерк на П2)) |
|
|
|
|
|
|||
П В, образованные вращением линии
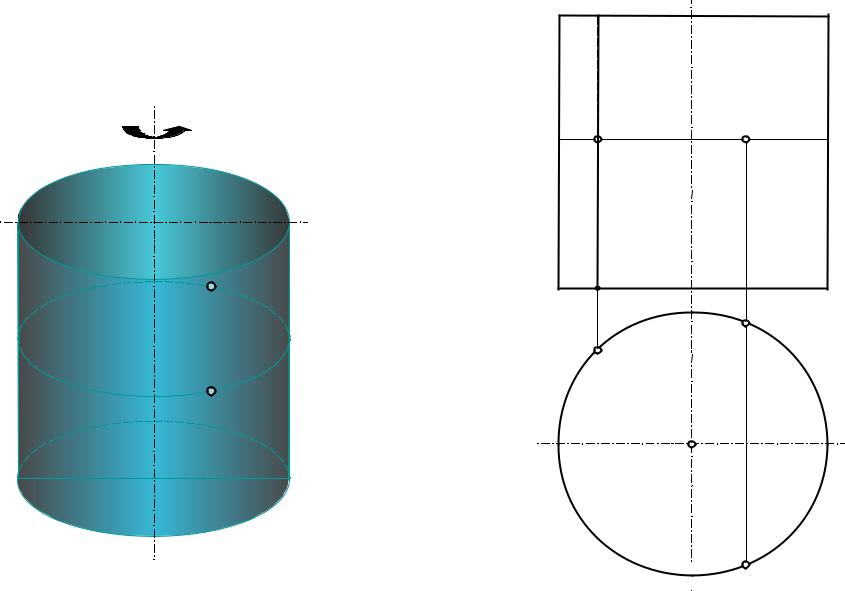
Прямой круговой цилиндр |
|
i2 |
|
Ф(а, i) a ││ i |
а – прямая |
|
|
|
i |
(A2) |
K2≡(K’2) |
|
|
||
|
a2 |
K’ |
K’1 |
|
A1≡a1 |
K |
|
|
i1 |
x2 + y2 = r2 |
|
K1 |
|
||
|
||
|
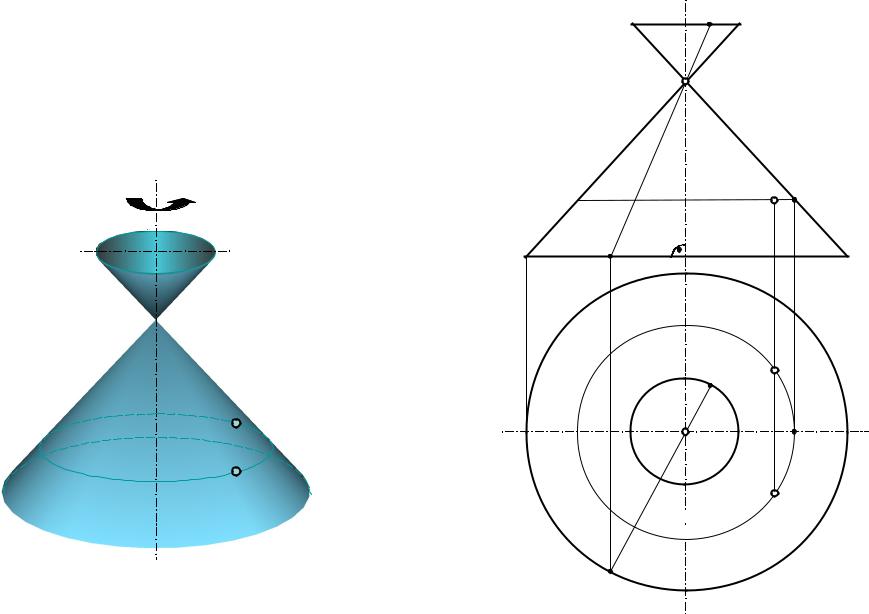
П В, образованные вращением линии
Прямой круговой конус
Ф(а, i) a ∩ i = s а – прямая
i
K’
K
z2 = k2 (x2 + y2)
i2
S2
a2 K2≡(K’2)
K’1
i1≡S2
a1  K1
K1

П В, образованные вращением линии
Гиперболоид |
Ф(а, i) |
а – гипербола |
a |
i |
|
i |
|||
|
|
|
|
|
|
|
i |
|
|
однополостной |
|
|
двухполостной |
|
b2z2 – a2(x2 + y2) = a2b2 |
|
|
b2(x2 + y2) – a2z2 = a2b2 |
|
|
|
|
|
|

П В, образованные вращением линии
Параболоид вращения
Ф(а, i) а – парабола
i
x2 + y2 = 2pz

П В, образованные вращением линии
a ││ i
Прямой
круговой
цилиндр
a  i
i
Гиперболоид Гиперболоид однополостной двухполостной
a ∩ i = s
Прямой круговой конус
Параболоид вращения

П В, образованные вращением
окружности
Сфера
Ф(а, i) а – окружность |
|
|
|
i3 |
|||
|
|
|
i2 |
a |
|
||
|
|
|
|
||||
|
a2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
t = 0
i
K2≡(K’2) |
(K’3) |
|
(K3) |
|
|||
|
|||
|
R
a1 |
(K’ ) |
|
1 |
 0
0
i1 



 (K1)
(K1)
x2 + y2 + z2 = r2

П В, образованные вращением окружности
Тор закрытый
Ф(а, i) а – окружность
t < R
i
t
R
(x2 + y2 + z2 + a2 – b2)2 = 4 a2 (x2 + y2), a < b
