4.8 Переходный процесс в электроприводе с двигателем независимого возбуждения при изменении магнитного потока

Обычно ДНВ работает при Ф=Ф_н если U=const или оно изменяется. Необходимость изменения (ослабления) потока возникает когда требуется получить скорость, превышающую основную (согласно требованиям технологического процесса). Пуск двигателя в этом случае совершается в дву этапа. Первый этап заключается в разбеге двигателя до основной скорости, соответствующей U=const и Ф=Ф_н, с выведением двигателя на естественную характеристику, а второй – в разгоне от основной до требуемой, которая достигается ослаблением магнитного потока.

Если бы поток изменялся мгновенно, то в начальный момент времени имел бы место бросок тока и момента и переход двигателя с одной характеристики на другую происходил так, как показано на рис. 4.8.1“а” и “б” пунктиром. Бросок тока и момента будет тем больше, чем быстрее темп изменения потока. В действительности поток изменяется во времени. Поэтому ток якоря и момент двигателя будут изменяться по т.н. динамической характеристике (кривые).

Для расчета переходного процесса пренебрегаем индуктивностью обмотки якоря L_Я ввиду ее малости по сравнению с индуктивностью обмотки возбуждения L_В.

С целью получения расчетного выражения воспользуемся уравнением равновесия ЭДС в якорной цепи и уравнением момента двигателя.

Выразим коэффициенты “k” через номинальные параметры двигателя, и подставим их в уравнения U и М.

;

1. ;

2. 

Определив из второго уравнения ток I_Я и подставив в первое, а также разделив обе части полученного выражения на , получим

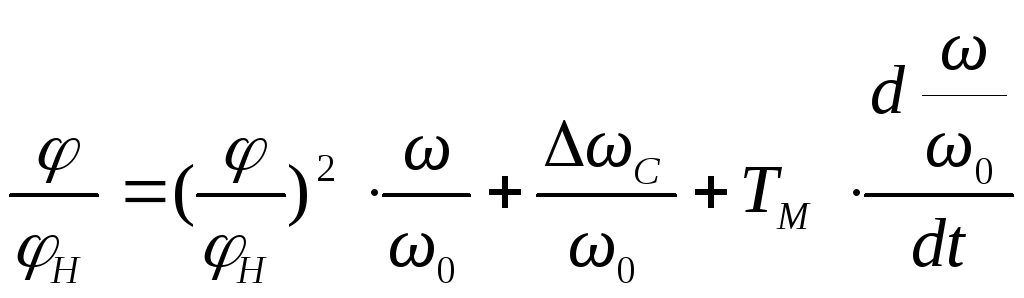
Или в относительных единицах

3. , где

;

Для решения этого уравнения нужно найти зависимость φ=f(t). На небольшом интервале изменения потока (рис. 4.8.2“а”) зависимость между Ф и i_b можно принять линейной, т.е. между Ф и i_в считать наличие пропорциональности .

При ненасыщенной магнитной системе, для которой характерна пропорциональность , уравнения равновесия ЭДС цепи возбуждения имеет вид:

Закон изменения тока возбуждения можно найти из этого уравнения

, где

При закон изменения потока будет таким же

, или в относительных единицах

Построив кривую φ=f(t), разбивает ее на участки постоянной длительности t. И на каждом участке поток считается постоянным, равным среднему значению (рис. 4.8.2“б”) так же как и скорость

, где

Имея зависимость φ=f(t) уравнение 3 можно решить в конечных приращениях, подставив в него значение и.

Окончательная расчетная формула имеет вид:

Расчет кривой скорости ведется с первого участка длительностью t, для которого известна и среднее значение потока. Приращение скорости на первом участке

Начальная скорость на втором участке длительностью t равна скорости в конце первого участка

Аналогично определяется скорость на втором участке и т.д. По рассчитанным приращениям строится кривая ν=f(t), которая изображена на рис. 4.8.3.

Для расчета и построения кривой I_Я=f(t) разделим обе части формулы 1 на U. Получим . Отсюда, где.

Примерный вид кривой I_Я=f(t) при М_с=const изображен на рис. 4.8.3. Конечное значение тока . Кривую изменения момента можно рассчитать и построить с помощью соотношения.

Расчет переходного процесса можно вести и в именованных величинах, используя формулы для приращения скорости .